turn restrictions
Turn restrictions specify a sequence of links in a network that vehicles are not allowed to drive. In the very simple case of a forbidden right-turn, the turn restriction would consist of two links describing the current link and the forbidden link leading right at the next node.
In MATSim, turn restrictions are described by link-attributes named
disallowedNextLinks with a value of type org.matsim.core.network.DisallowedNextLinks.
The following concept for modelling turn restrictions in MATSim was developed by Marcel Rieser (Simunto) and Hannes Rewald (Volkswagen Group) in October 2023 during the MATSim Code Sprint week in Berlin.
-
starting link is a link that has an attribute
disallowedNextLinks, i.e. a link where a turn restriction starts. -
turn restriction describes a sequence of links that agents are not allowed
to fully travel along from a given starting link.
Such a sequence must always contain at least 1 link, i.e. a forbidden next link. The starting link is not part of the link sequence, as it is implicitly given.
If a sequence has 2 or more links, agents are allowed to travel a part of the sequence and then continue on other links not part of the sequence. Example: Given a sequence of three links, an agent can drive along the first two links and then make a turn, so it doesn't continue on the third link. In other words: Agents are allowed to drive along parts of that sequence, but not the complete sequence of links. - affected links are all links that are part of any turn restriction, i.e. part of the sequence of links that build a turn restriction, including the starting link.
- colored links are copies of existing links in the network, but relevant to the turn restritions starting on a specific link only.
- colored nodes are copies of existing nodes in the network, but relevant to the turn restrictions starting on a specific link only.
To visualize examples, a grid-like network is used with 4 × 4 nodes.
The nodes are labelled with capital letters starting from A, while the links
are labelled with small pairs of the letters of the nodes connecting (see Figure 1).
Affected nodes are shown hollow with a border, while regular nodes are displayed
filled (see Figure 2). Colored nodes (effectively copies of existing nodes) are shown with an
offset near their original nodes, as are colored links (see Figure 3).
Figure 1: Network used for examples
Figure 2: Network elements used in examples
For each link with turn restrictions, create a sub-graph of the network containing all links required to model all allowed paths, but exclude the last link of turn restrictions' link sequence to enforce the "disallow" along that route.
Given a single starting link with one or more turn restrictions:
- Determine the set of end-links E of all turn restrictions' link sequences last links.
- Determine the set of affected-links L, i.e. all links part of a link sequence plus the starting link.
- Determine the set of affected-nodes N, i.e. all from-nodes of links in the link sequences building the turn restrictions.
- Create copies of all nodes in N as colored nodes.
- Create copies of all out-links of nodes in N as colored links. If the out-link is part of E, ignore it. If the out-link is part of L, connect its colored copy to colored nodes as from- and to-nodes. If the outlink is neither part of E or L, use a colored node as from-node, but the original (non-colored) node as to-node.
- Replace the starting link with a colored link, using the regular from-node but leading to the colored copy of the to-node.
Figure 3: Example of applying a single turn restriction
Figure 4: Example of applying two turn restrictions starting on the same link
The algorithm outlined above works well for turn restrictions that don't overlap each other. As soon as one turn restriction has an affected link that is also the starting link of another turn restriction, this additional restriction must also be taken into account.
Thus, the algorithm needs to be adapted, resulting in the following algorithm to apply all turn restrictions in a network while taking interactions between turn restrictions into account:
Given a link with turn restrictions (e.g. by iterating over all links
in a network and handle all links with an attribute disallowedNextLinks):
- Determine the set of end-links E of all turn restrictions' link sequences last links.
- Determine the set of affected-links L and the set of affected-nodes N. Start by following each link sequence link-by-link. If a link was replaced by a colored link, add the colored link to L, otherwise the regular link. If the to-node of a link is a colored node, add the colored node to N, otherwise the regular node. Use the out-links of the added node to look for the next link of the link-sequence and add it to L. This can again be either a regular link or a colored link. Continue until you reach the end of the link sequence. Repeat it for each link sequence if the link has multiple turn restrictions.
- Create copies of all nodes in N as (newly) colored nodes, even if it is already a colored node.
- Create copies of all out-links of nodes in N as colored links. If the out-link is part of E, ignore it. If the out-link is part of L, connect its colored copy to colored nodes as from- and to-nodes. If the out-link is neither part of E or L, use a colored node as from-node, but the original (potentially colored) node as to-node.
- Replace the starting link with a colored link, using the regular from-node but leading to the colored copy of the to-node.
- If the starting link has other colored copies except the one just added
in step 5, then re-apply steps 2 to 5 with the colored link as starting link.
In this case, due to the previous turn restrictions applied, not all
affected links might be available anymore.
Optimization: Iff the colored link has a non-colored toNode, the existing colored link can be changed to re-use the same colored to-node of the replacement link created in step 5, instead of re-applying the whole turn restriction.
Figure 5: Example of applying turn restrictions from two starting links
Applying the green turn restrictions first, then the red:
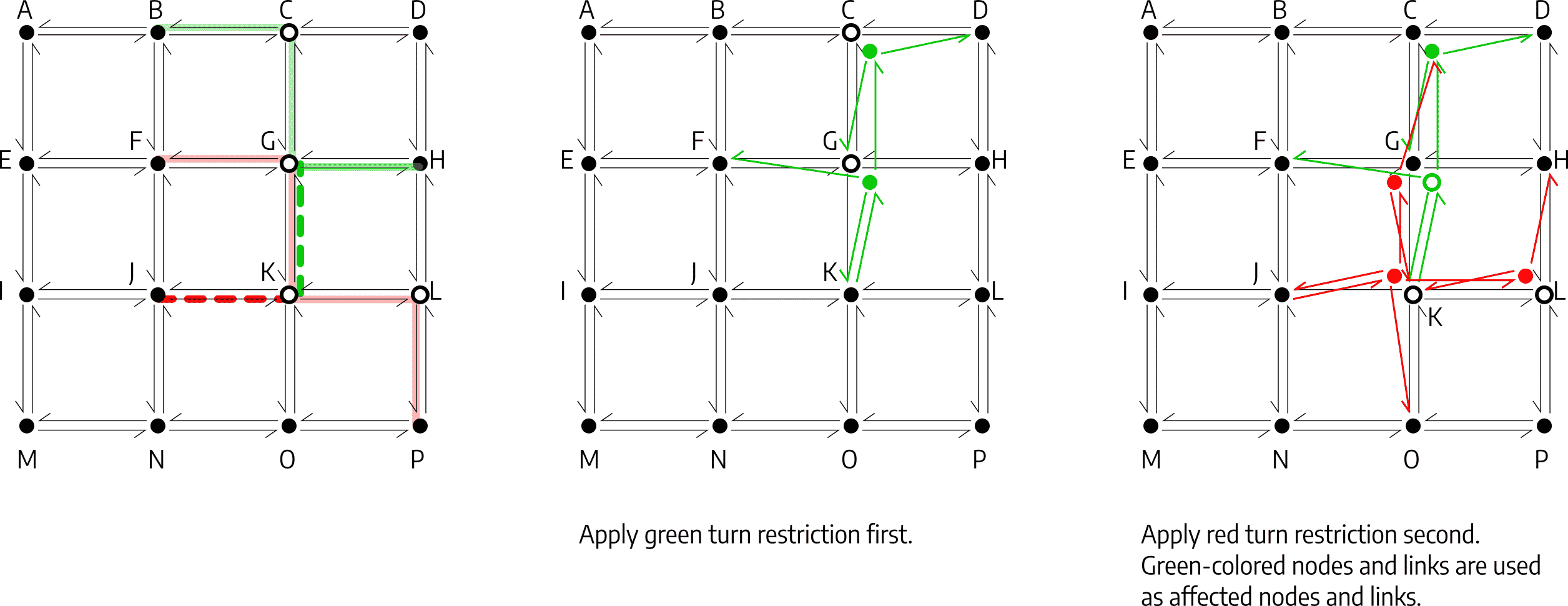Figure 6: Applying the green turn restrictions first
Applying the red turn restrictions first, then the green. Note how a part of the red sub-graph becomes inaccessible.
Figure 7: Applying the red turn restrictions first
With different turn restrictions, first applying the red restriction and second the green restriction, shows how the optimization mentioned in step 6 works:
Figure 8: Optimization when applying a turn restriction to a colored link leading to a non-colored node
Each colored sub-graph is only reachable by the single colored link replacing the starting link. As all the links in the sub-graph are directed and do not build any loops, the subgraph effectively builds a tree structure. Replacing any link with a newly colored link as outlined in step 6 in the algorithm above, effectively cuts off a part of the tree, making parts of the subgraph inaccessible.
Thus, instead of using the previously colored subgraph as starting point for a newly colored copy in step 6, the previously colored subgraph can be re-used and be re-colored instead. If the previously colored subgraph does not contain a colored node for an affected node, a colored node from step 3 should be used if available, or a newly colored node be created. If a newly colored node is re-used, processing the along this link-sequence can be stopped.
If re-using and re-coloring a subgraph, care must be taken to potentially remove end links from the existing subgraph, instead of not adding it as a copy as outline in step 4 of the algorithm.
The re-use of colored sub-graphs leads to a graph with less nodes and links, but adds complexity when creating the routing-graph.
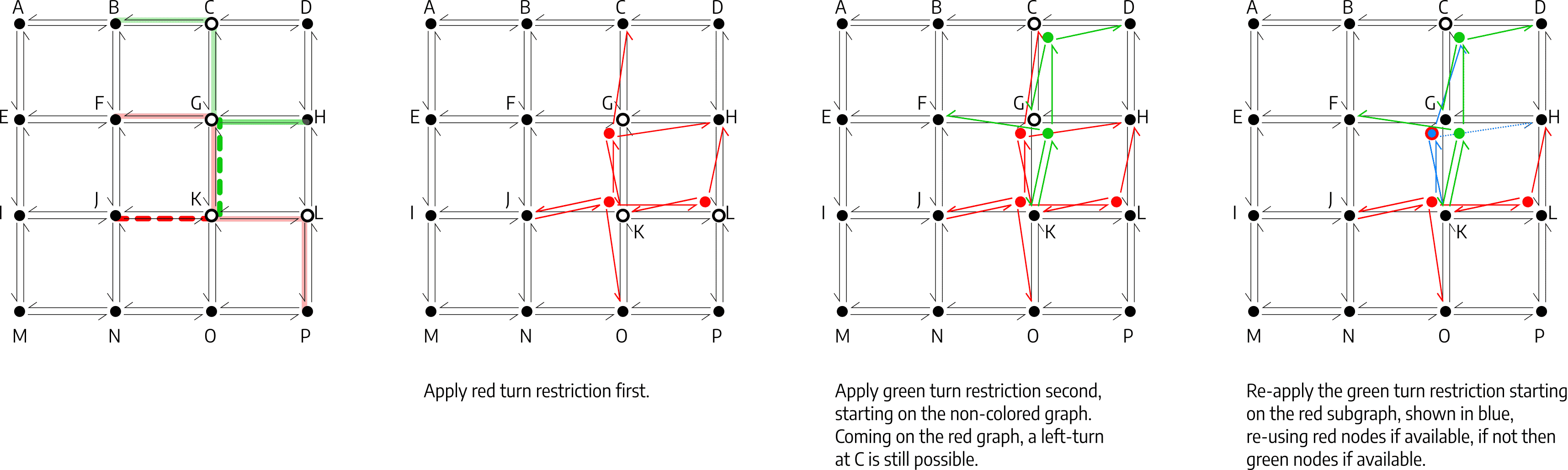Figure 8: Applying the red turn restrictions first, re-using a sub-graph