理解卷积.md

Understanding Convolution

在ConvNets中，构建卷积神经网络的理解，不涉及任何重大的数学运算。进一步深入的话，死活都得理解卷积的数学原理。

如果大家只是想理解卷积神经网络，粗略领会卷积计算就足够啦。但是，本系列的目标是带领大家走在卷积神经网络的前沿并探索新的选择（可能）。为达到这个目标，就必须非常深入的领悟卷积的数学原理。

谢天谢地，只需要举几个例子，卷积就是清晰的概念。

向坠球学习

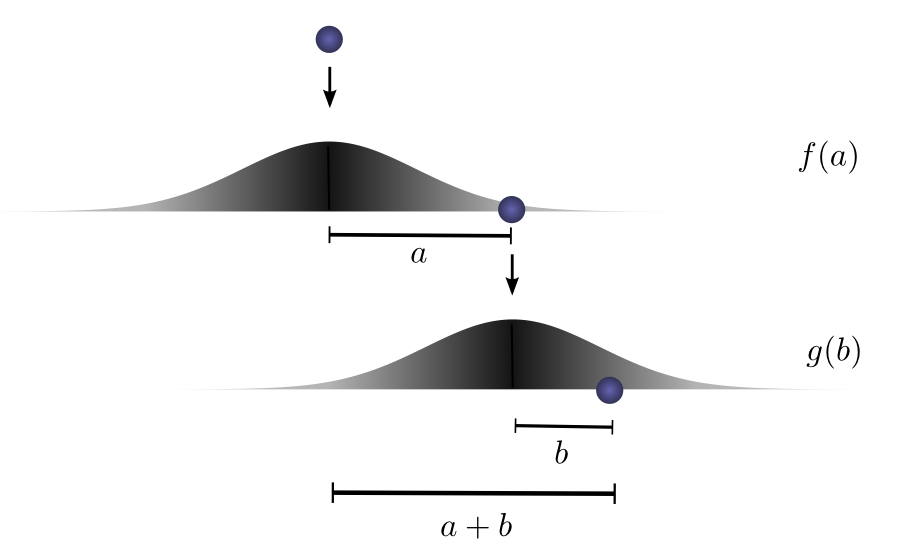
想象，把一个球从某个高处丢落到地面，此时球仅做一维运动。球滚动的距离是多么相似啊！

一起分解下：

第一次掉落，球滚动到距离起始点 $a$ 单元距离的点，概率是 $f(a)$ ，这里的 $f$ 是概率分布。

之后，把球以另外的高度——就是上一次高度——丢落，这次球滚动到距离此次起始点 $b$ 单元的点，概率是 $g(b)$ ，这里的 $g$ 是不同的概率分布，如果这次球是从不同的高度跌落的（考虑空气流动等随机因素）。

如果固定第一次跌落的结果，大家知道的，球行进一段距离 $a$ ，为了让球行进一段总距离 $c$ ，第二次行进的距离也固定为 $b$ ，当然， $a + b=c$ 。因此球两次跌落行进距离综合等于 $c$ 的概率是 $f(a)g(b)$ 。

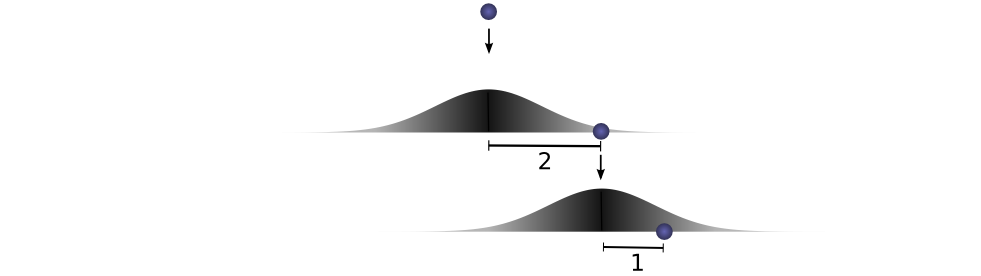
把上述指代的数量给定，举个例子。想让球两次跌落行进距离为 $3$ ， $c$ 。如果第一次行进了 $2$， $a$ ，第二次必须行进 $1$ ， $b$ ，是为了达到设定的总行进距离为 $3$ ， $a + b$ ，发生概率是 $f(2)g(1)$ 。

然而，这并非是获取总距离 $3$ 的途径。球可以先走 $1$ ，后走 $2$ ，或者先 $0$ ，后 $3$ 。可以先后走任意距离，只要加起来是 $3$ 。

概率分别表示为 $f(1)g(2)$ 和 $f(0)g(3)$ 。

为了找到球行进达到距离 $c$ 的可能性总和，大家不能只考虑某一种达到 $c$ 的可能，相反，必须考虑把 $c$ 分割为两部分 $a$ 和 $b$ 的全部可能的途径，把概率累加起来： $$...~~ f(0)!\cdot! g(3) + f(1)!\cdot! g(2) + f(2)!\cdot! g(1)~~...$$

大家已经知道每个满足 $a + b=c$ 情况的概率很简单： $f(a)g(b)$。因此，把 $a + b=c$ 的每个解决方案累加起来，可以把可能性表示为： $$\sum_{a+b=c}f(a)g(b)$$

事实证明，所做的正是卷积！

特别地， $$ 和 $$ 的卷积，以定义好 $c$ 的情况下评估： $(f*g)(c)=\sum_{a+b=c}f(a)g(b)$

如果用 $b=c - a$ 则得到： $(f*g)(c)=\sum_af(a)g(c - a)$

上式是卷积的标准定义。

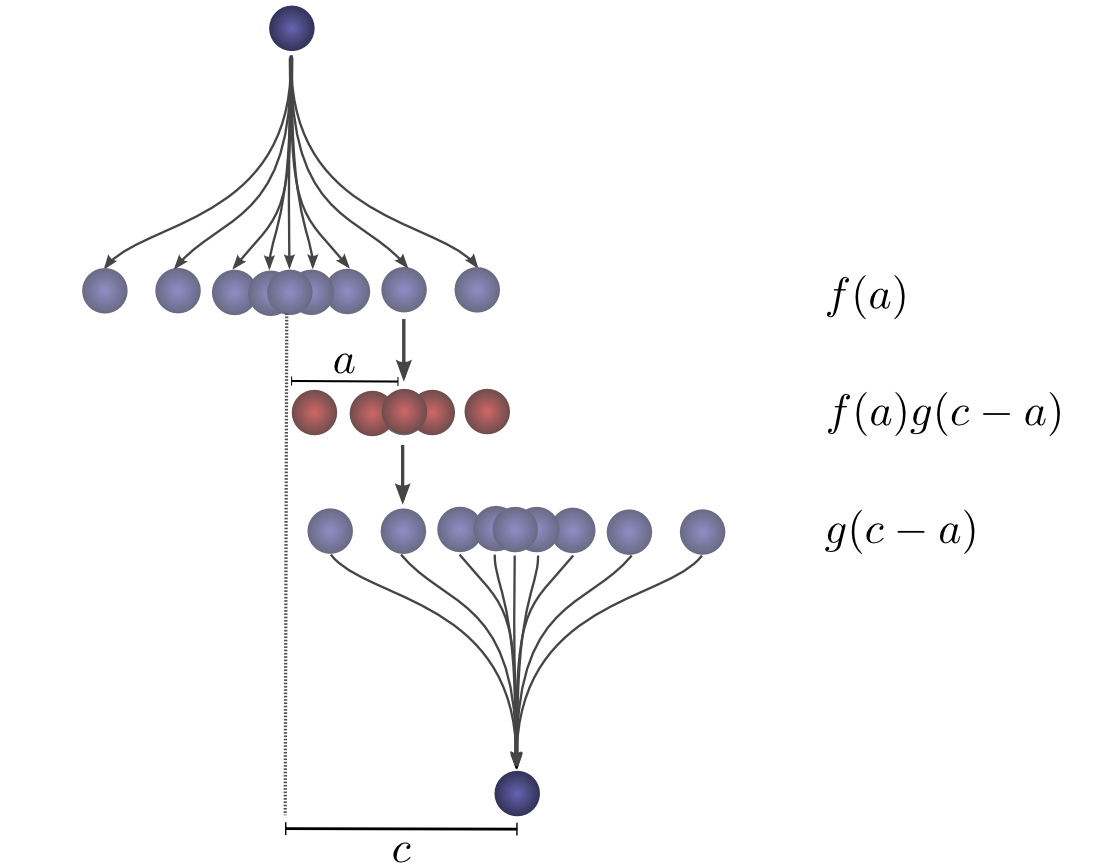
为使这个公式更具体（concrete），大家可以思考球落脚点的关系。第一次跌落以 $f(a)$ 的概率落在 $a$ 的中间点。如果确实落在 $a$ 点，最终落在 $c$ 点的概率是 $g(c - a)$。

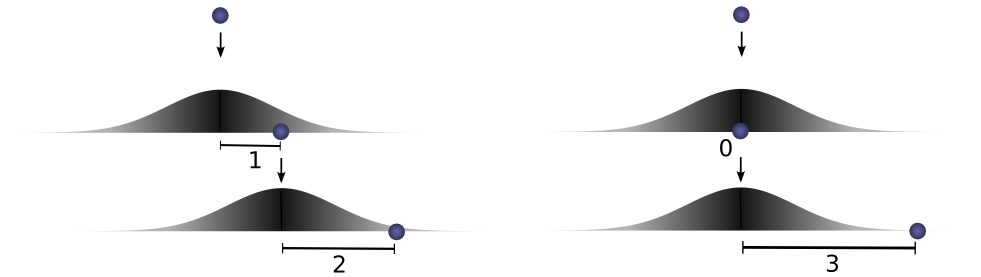
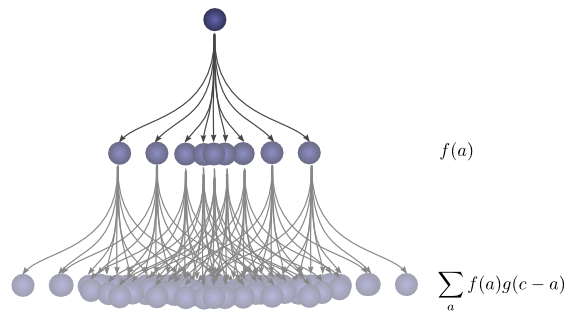
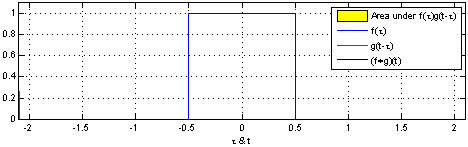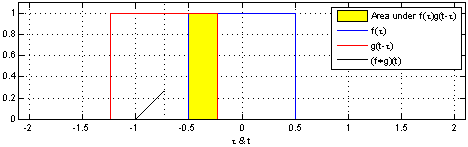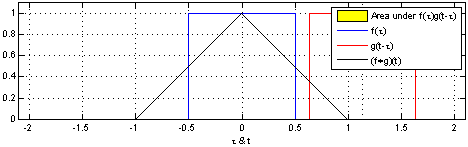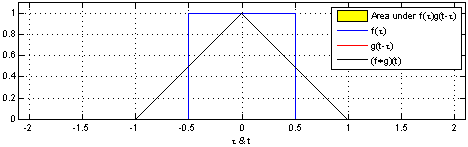
为得到卷积结果，考虑全部中间的点。

卷积可视化

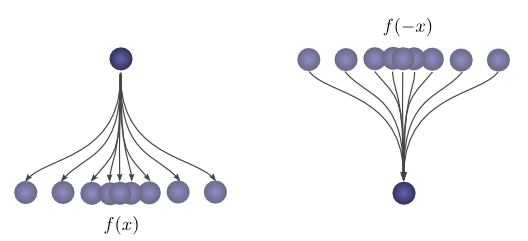
这儿给出一种很美的花招让思考卷积更容易。

首先，观察。假定球行进距离起始位置距离为 $x$ 的概率是 $f(x)$ 。

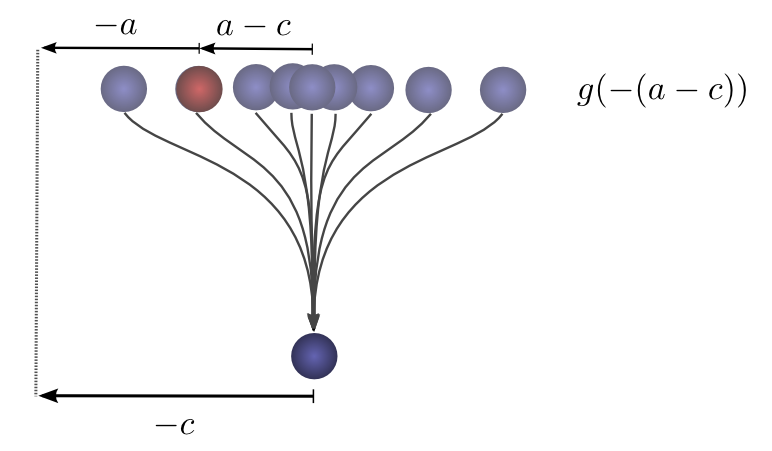
接着，之后，球自落脚点回滚一段距离 $x$ 的概率是 $f(-x)$ 。

如果大家知道球在第二次跌落后落脚点距离最初起始位置距离是 $c$ ，那第一次落脚点距离起始点是 $a$ 的概率是什么？

上图表明，这个概率是 $g(-(a - c))=g(c-a)$ 。

现在，考虑球滚落到距离最初起始位置为 $c$ 的店的每种中间点的可能。

大家清楚第一次掉落在距离起始点为 $a$ 的概率是 $f(a)$ ，也知道如果最终落在距离最初起始位置为 $c$ 的点时第一次落在距离起始位置为 $a$ 的概率是 $g(c - a)$ 。

累加所有 $a_i$ ，就是卷积结果！

这种方法的优势就是允许大家在单张图上可视化球行进总距离为 $c$ 的卷里评估。

通过移动下半部分，就可以做到。这样大家以整体领悟卷积。

举个例子，可以看到峰值的分布排列。

并且以分布间的交集收缩变小。

通过在动画中运用这个窍门，可视化理解卷积真的成为可能。

下图展示两个窗口函数之间的卷积过程：

站着这个视角，很多事情变得更直观。

大家来考虑一个非概率的例子。卷积某些时候用于音频合成，如可能用有两个尖峰其余静默的函数、或创造回音。因为双尖峰函数滑动，一个尖峰首先实时碰到一个点，并叠加信号到输出声音，之后另一个尖峰跟随，添加第二个延迟的副本。

高维卷积

卷积是极其一般的概念，大家也可以应用到更多维度。

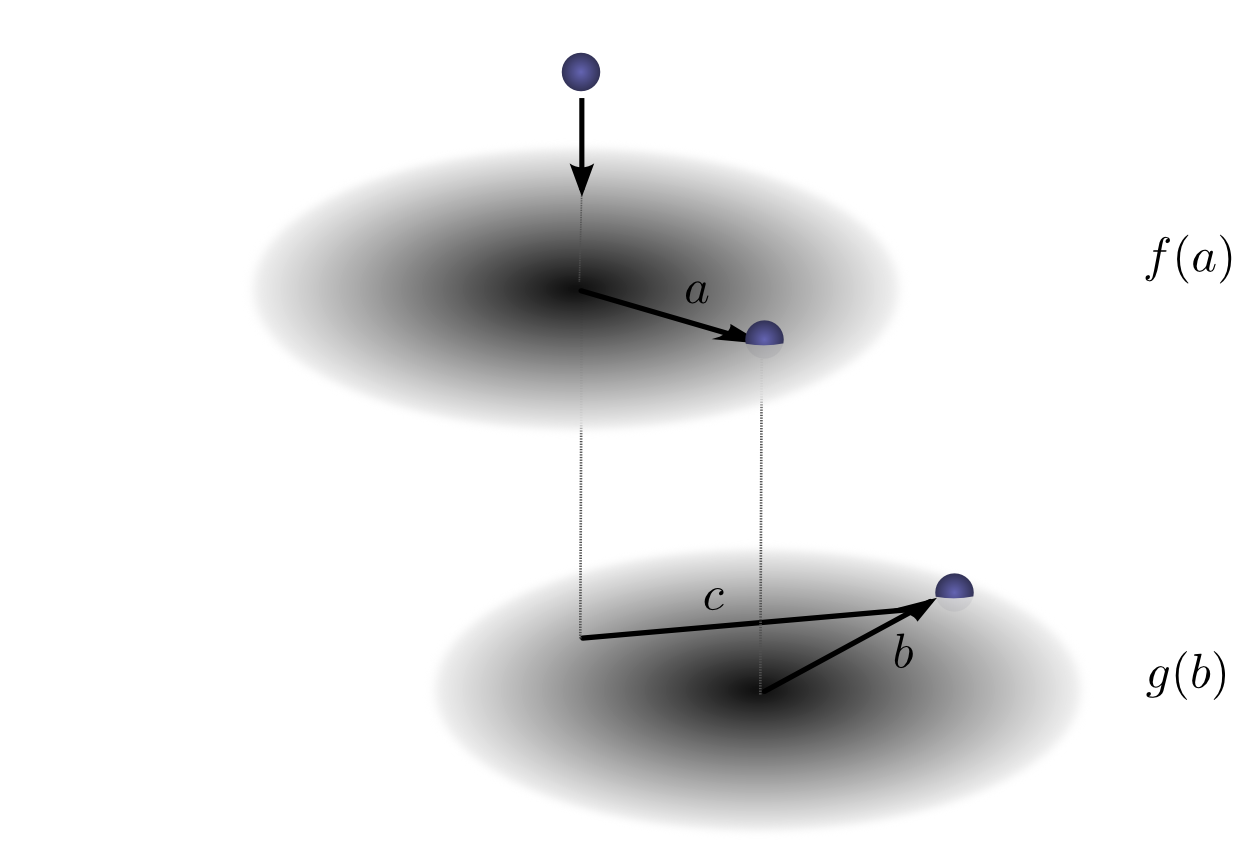
再次考虑一个球跌落例子，先在，球跌落后不只滚到到一个方向，而是两个。

和之前一样，卷积表示为： $$(f*g)(c)=\sum_{a+b=c}f(a)g(b)$$

不同的是，现在的 $b$ 、 $b$ 和 $c$ 都是向量，更直白地表示： $$(f*g)(c_1,c_2)=\sum_{a_1 + b_1=c1 ~\ a_2 + b_2=c_2}f(a_1,a_2)g(b_1,b_2)$$

或以标准定义的方式呈现： $$(f*g)(c_1,c_2)=\sum_{a_1,a_2}f(a_1,a_2)g(c_1 - a_1,c_2 - a_2)$$

正如一维卷积，大家可以把二维卷积想象成在一个函数上滑动另一个函数，乘和加。

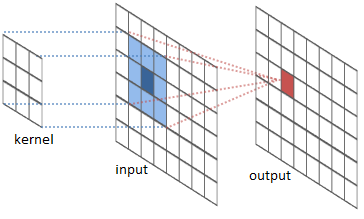
常用的就是图像处理，可以认为图像就是一个二维函数，很多重要的图像变换就是把图像函数和一个局部的小函数（卷积核）作卷积（convolve）。

卷积核滑动到图像的每一个位置、计算出一个新的像素，即卷积核所覆盖的像素加权和。

例如，一个3x3的平均卷积核，可以让图像模糊。卷积核通过将所覆盖的九个像素的均值作为卷积核中心对应的像素。

还可以通过把毗邻的像素其中一个取反别的取零来检测边缘，就是让相邻像素作差。当相邻像素值接近，给出近似零。有边缘的地方，垂直边界方向的相邻像素差别很大。

查看GIMP有很多别的样例。

卷积神经网络

总结

本文介绍了一堆数学机制，却可能并不清晰。显然卷积是概率论和计算机图形中有用的工具，可是大家从卷积神经网络短语的数据卷积重获取到什么？

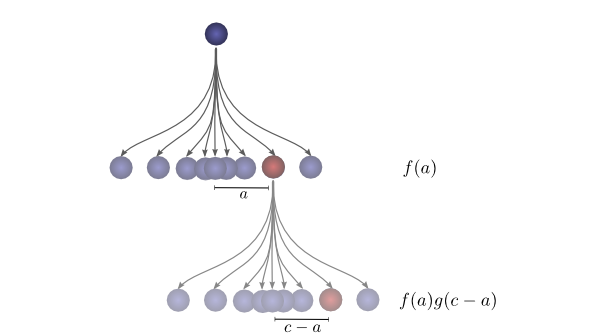
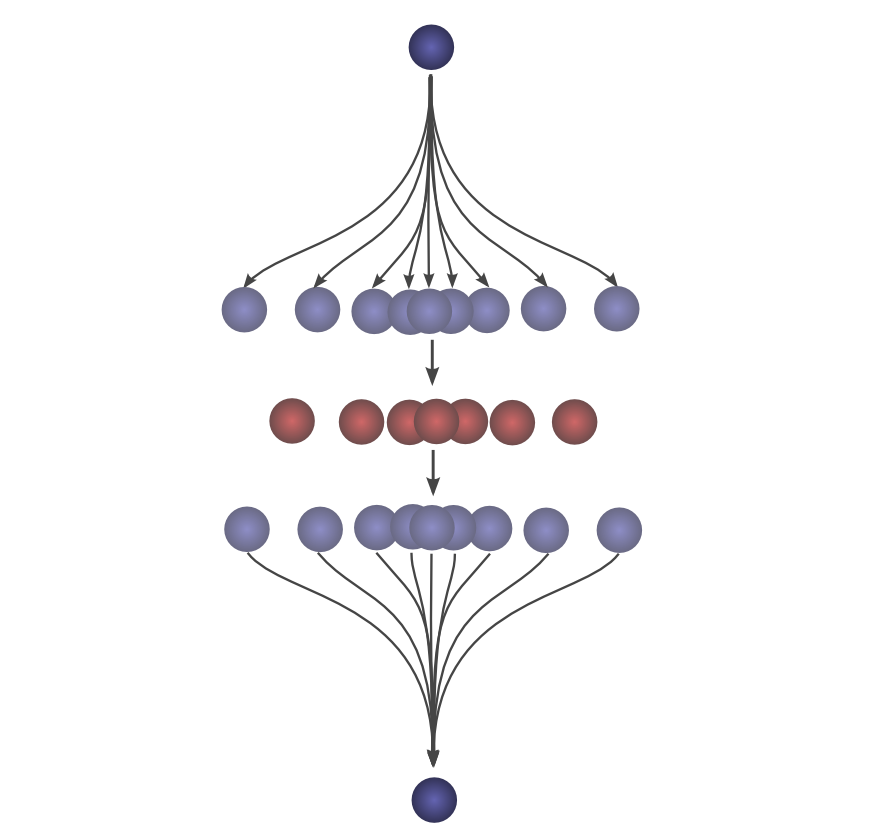
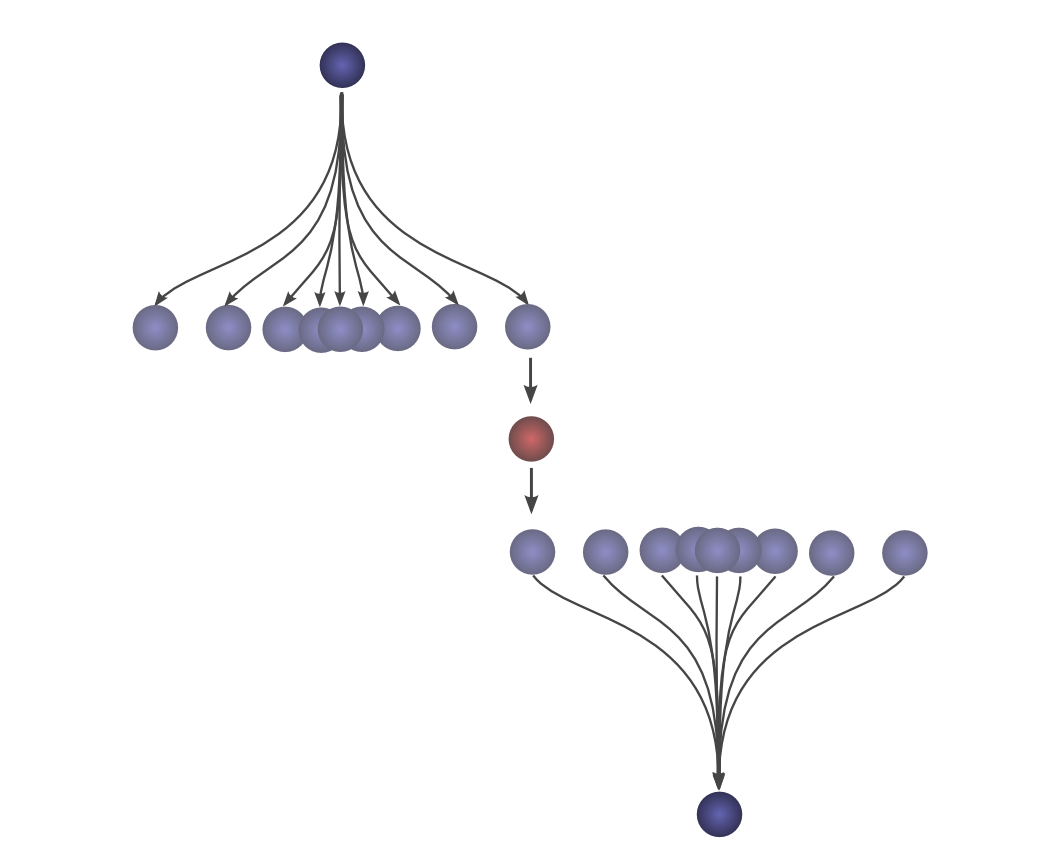
首先，卷积是描述网络连线非常强大的语言，截至目前涉及的样例还没复杂到因此获益（变的清晰），然而，卷积可以拜托大量记账簿式的混乱。

其次，卷积与生俱来意义重大的实现应用，很多提供高效卷积运行时的库，进一步讲，因为朴素卷积大致是 $O(n^2)$ 的时间复杂度操作，采用某些相当深奥的数学洞悉，可能构建时间复杂度为 $O(n\log(n))$ 的实现。

最后，事实上基于多GPU的并行高效卷积实现在计算机识别领域近期已经取得进展。

补充

---