ConvNets.md

Conv Nets: A Modular Perspective

作者以模块化视角剖析卷积网络。

简介

近几年，深度神经网络导致很多模式识别问题突破性进展，例如计算机视觉和语音识别。导致这些成果最本质的因素之一就是一种特殊的神经网络，叫做卷积神经网络。

最简单的，卷积神经网络可以看作一种复用很多同一神经元副本的神经网络。这使得网络在保持实参数量的前提下提供多神经元来表达计算机的大型模型，这些实参描述神经元的行为，应该学习得非常小（that need to be learned fairly small）。

具有同一神经元的多个副本，这个花招大致类似数学和计算机科学中函数的抽象概念。

编程时，大家写一次函数，多处调用，而不用把相同的代码在不同的地方写上好多遍，这让编程变得高效、健壮（导致更少的问题）。

类似地，卷积神经网络可以学习一个神经元一次、然后很多地方使用，使得训练模型变得容易且降低错误。

卷积神经网络结构

假定读者想得到一个神经网络，盯着音频样本、预测有人说话否。

或许还想做更多的分析，如果有人说话。

读者实时获取音频样本的不同点，样本是均匀分布的（evenly spaced）。

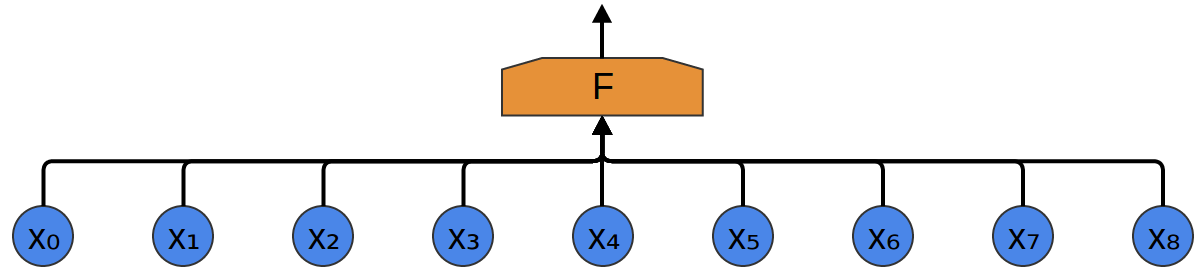
用神经网络给这些样本分类的最简单方式就是直接将这些样本连接到一个全连接层。

全连接层是一群不同的神经元，每个神经元都连接到每个输入。

一个复杂点的方法注意到属性的某种对称性对寻找数据有用。

大家更多地关注数据的局部属性：

• 给定时间内声音的频率如何？
• 声音的频率降低或升高否？

大家实时关注所有样本的同一个属性。

一开始就知道声音的频率是有用的，了解中间的声音频率是有用的，清楚结尾的声音频率也有用的。

此外，注意到这些都是局部属性，只需要考虑音频样本一个小的窗口就可以做出检测。

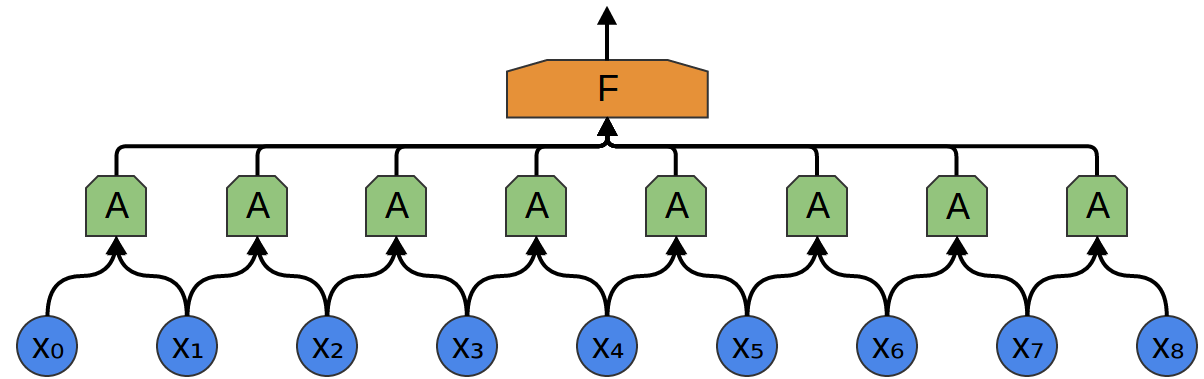
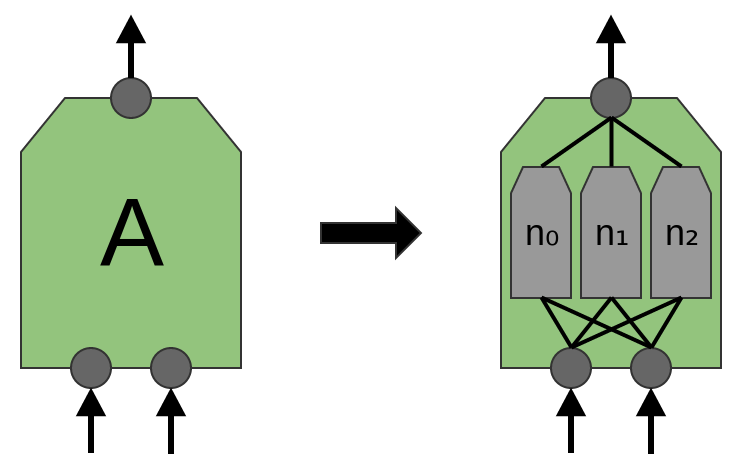
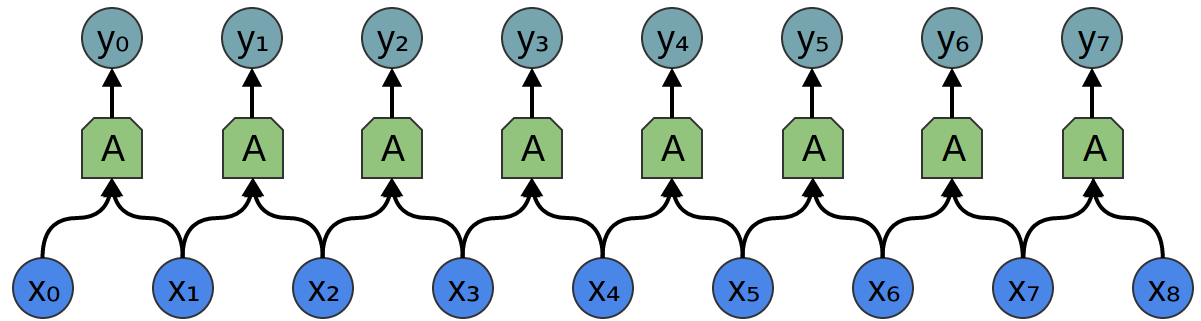
因此，可以创建一组神经元， $A$ ，它能盯住数据样本的一小段。

对的，$A$ ，盯紧全部这中片段、计算确定的特征。

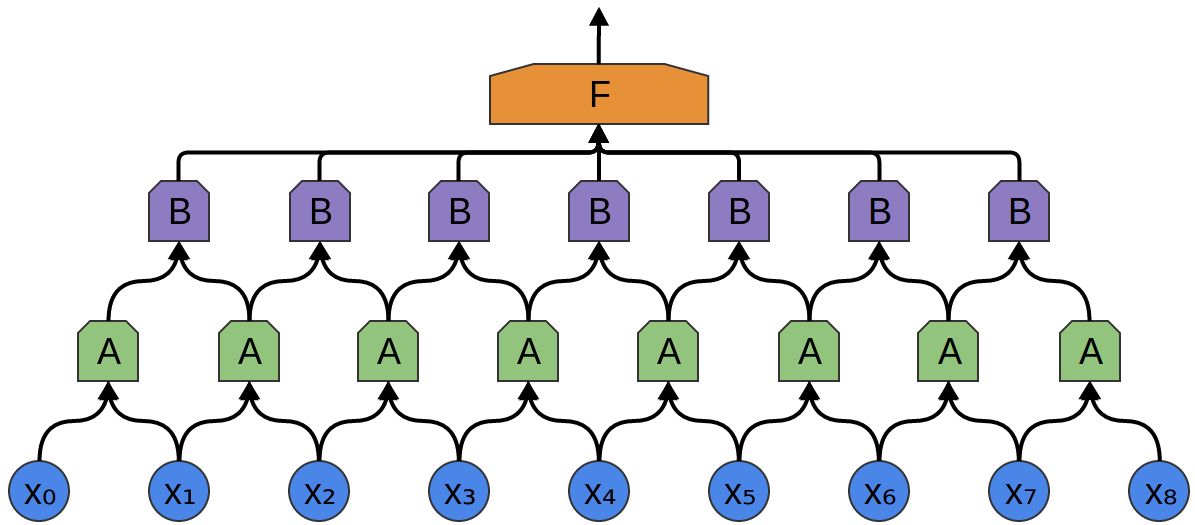
然后，该卷积层的输出反馈到一个全连接层， $F$ 。

上述例子中， $A$ 只关心的片段包括两部分，这不现实！

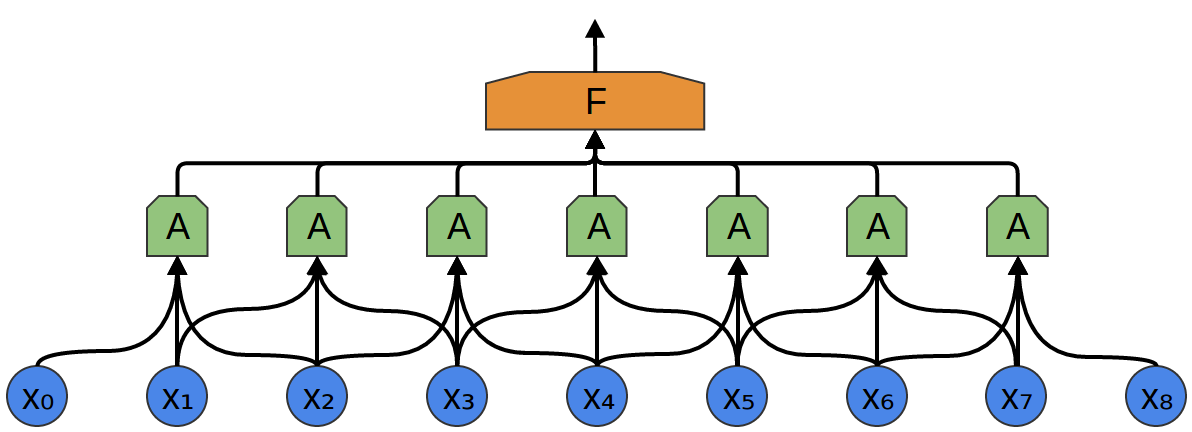
通常，一个卷积层的窗口应当更大。

接下来的例子， $A$ 关注三个点，这也不现实！

悲哀，这是示意 $A$ 连接到多个点的把戏。

卷积层的一个非常帅的属性就是自身的组成。

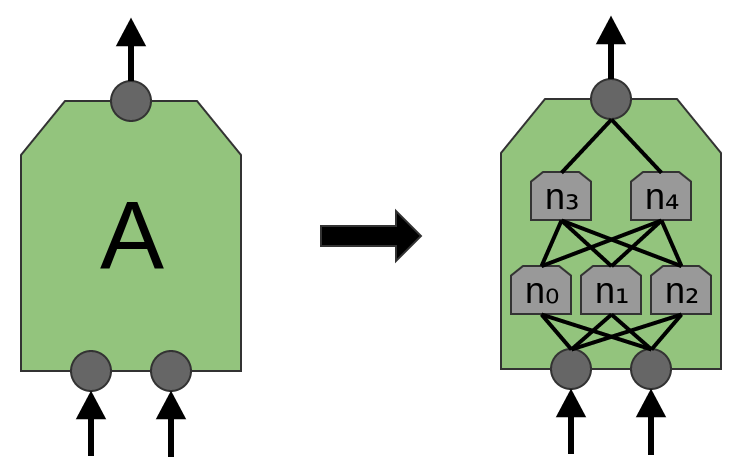
设计者可以把一个卷积层的输出反馈到另一个层。

网络中的每一层，都可以检测更高级的、更抽象的特征。

接下来，将有一组神经元， $B$ ，用来创建另一个卷积层，堆叠在之前那个卷积层的上边。

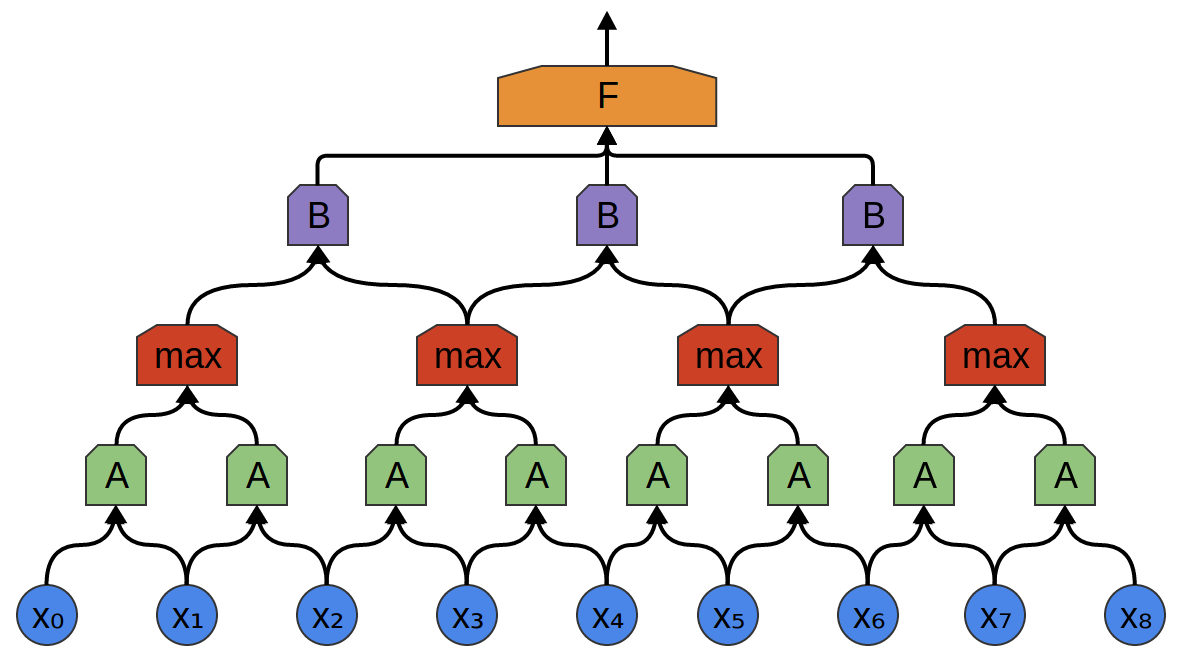
卷积层之间经常夹杂着池化层。

特别是一种叫做“最大池化”的层，非常流行。

通常，从高级视角来看，大家不关心一个特征所代表的精确度。

如果音频样本的频移或早或晚地轻微发生，那真的没关系么？

一个最大池化层采用前一层小块特征的最大值，输出表明前一层的一个区域中出现该特征否，但位置不精确。

最大池化是种“缩小”，允许后续的卷积层在更大的数据片段上工作，因为池化后的一小片对应池化前的一大片。这让大家对一些很小的数据转换不变（invariant：去抖动）。

之前的例子中，应用一维卷积层。然而，卷积层也能对多维数据起作用。

事实上，卷积神经网络最著名的成就就是应用二维卷积神经网络来识别图像。

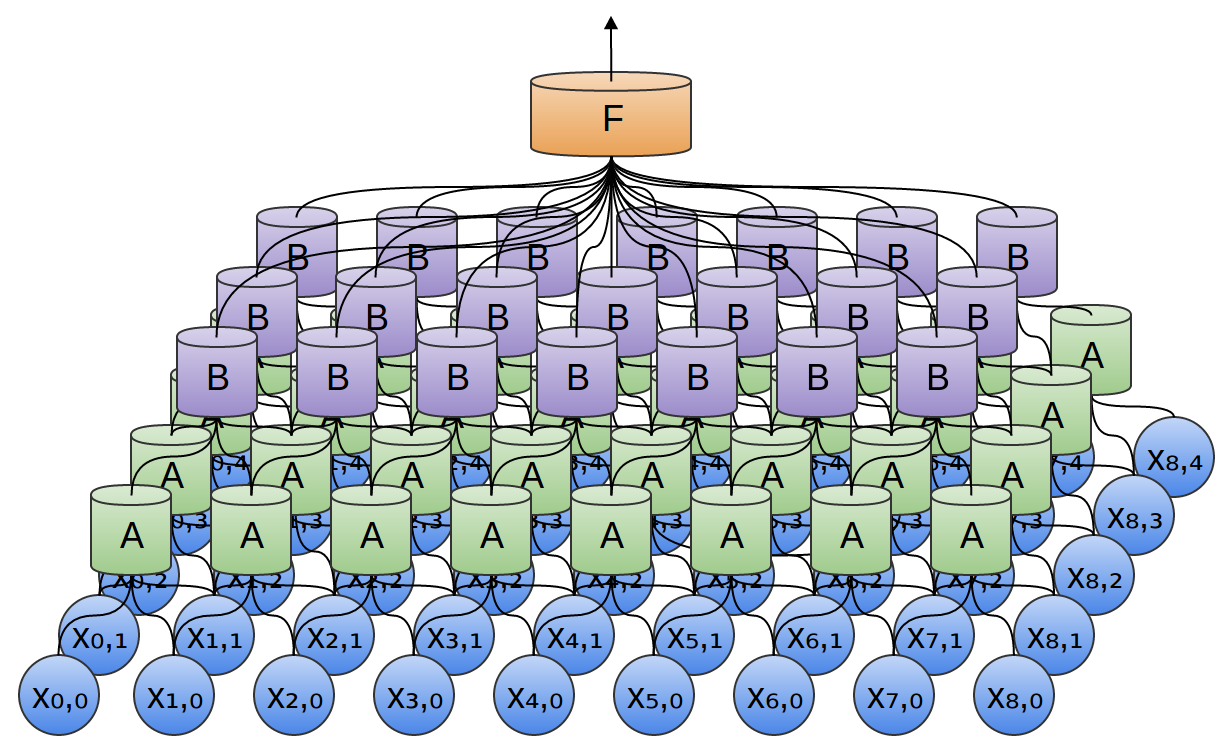
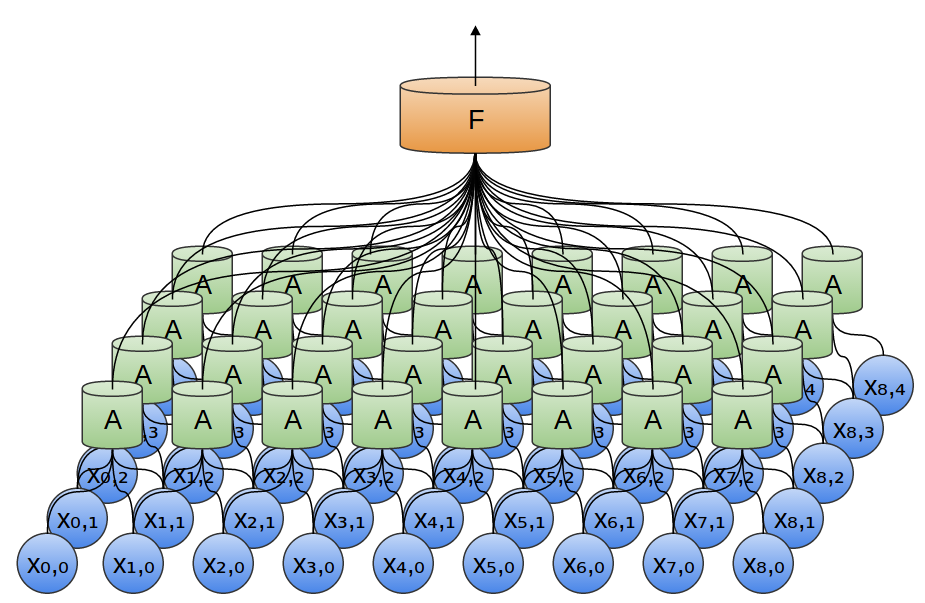
在一个二维卷积层， $A$ 关注块而非片段。

对于每个块， $A$ 将计算其特征。例如，可能学习检测边缘的存在，或检测文本，或对比两种颜色。

前例中，把卷积层的输出反馈到一个全连接层。

但是，也可以编排两个卷积层，向一维情况一样。

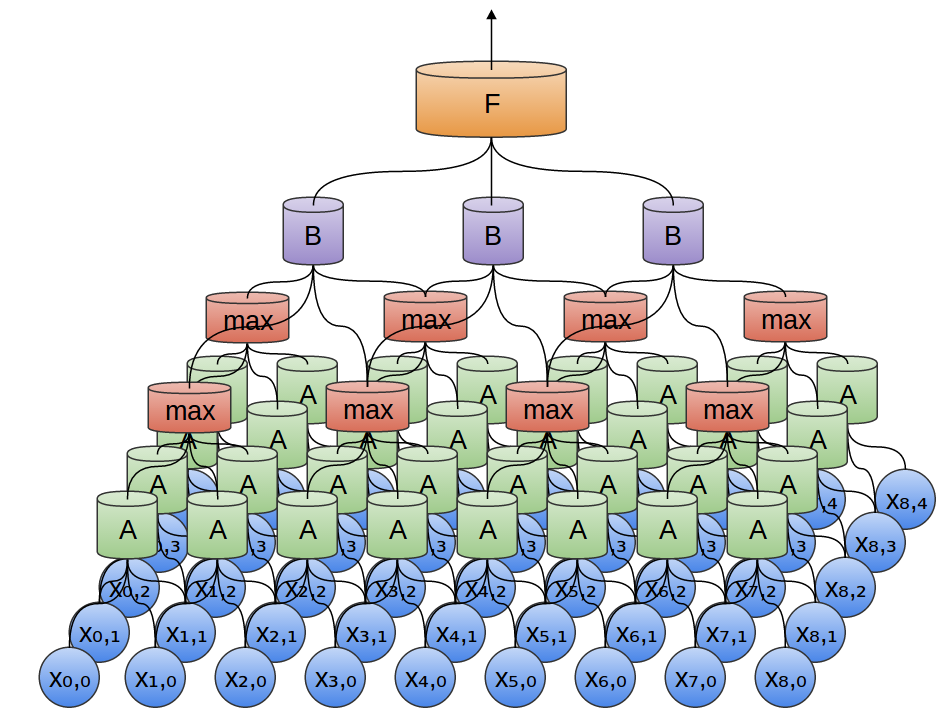
也可以二维做最大池化。这里，取出一小块的特性的最大值。

归结起来，大家关心一整幅图片，不关心一个边缘的精确点、小到一个像素。

搞清楚在哪一小片像素内就足够了。

三维卷积网络有时也会用到，像视频或立体数据（3D医学扫描）。

然而，三维的应用并不多，且很难可视化。

现在，如前所述， $A$ 是一组神经元。大家应当再准确一点： $A$ 究竟是什么？

传统的卷积层， $A$ 是一束并行的神经元，有相同的输入、计算不同的特征。

例如，一个二维卷积层中，某个神经元可能检测水平边缘、另外的神经元可能检测垂直边缘，别的神经元可能检测红绿色比。

即便如此（that said），近期的论文“网络嵌套（Network in Network）”，提出一个新层“Mlpconv”。该模型中， $A$ 应当有多层神经元，最后一层输出该区域的高级特征。论文的模型达到某种令人十分钦佩的结果，在一许多基准数据集合上创造新的“艺术境界”。

即便如此，着眼本文的目的，将聚焦各标准卷积层，再此考虑这些已经足够。

卷积神经网络结果

早些时候，笔者提到在计算机视觉采用卷积神经网络取得的最新突破。继续之前，笔者愿意简短地论述某些成果作为动力。

在2012年，Alex Krizhevsky，Ilya Sutsskever及Geoff Hinton放风水面外已存在图片分类成果（blew existing image classification results out of the water）。

三位的进展是把一群不同的片结合在一起的结果，使用GPU集群训练一个非常大型的、深度的、神经网络，采用一种新的神经元（ReLU）和一种新的技术降低过拟合问题（Dropout），利用以组十分大的拥有众多图片分类的数据集合（ImageNet），当然，这是一种卷积神经网络。

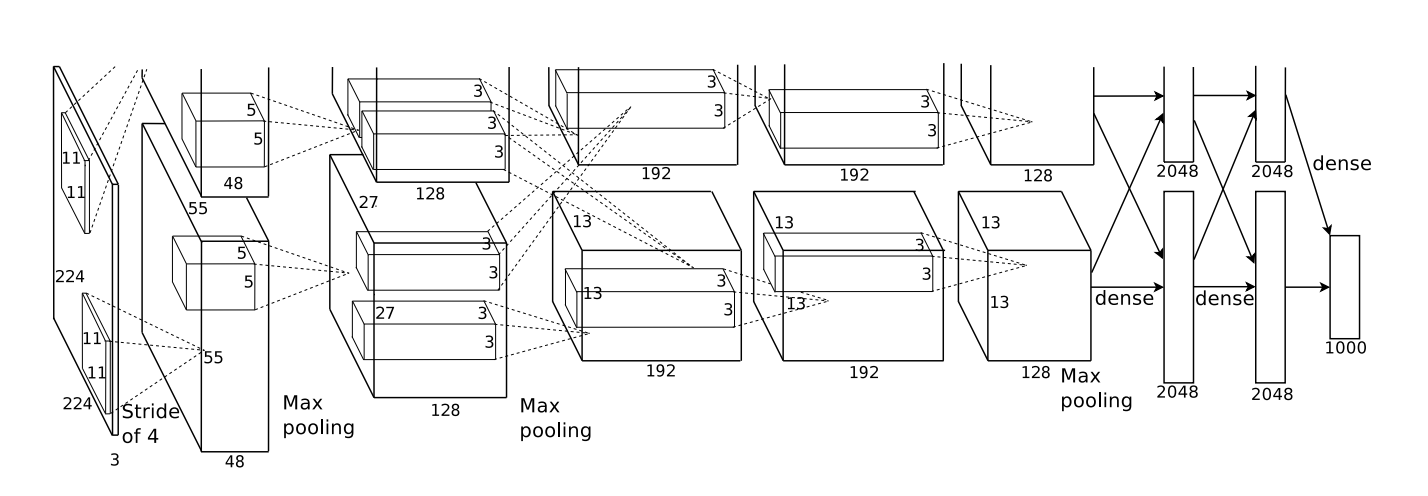
三位的架构，示意如下，非常深度的。拥有5个卷积层，点缀着池化层，还有3个全连接层。早期的层分离到2块GPU上。

三位训练该网络来把图片分类为上千种不同的种类。

随机猜测，当时一般模型猜对的概率大概是千分之一，而AlexNet能达到百分之六十三！做五次猜测就有一个是正确答案的概率更高达百分之八十五！

甚至它的某些错误对笔者来说似乎相当合乎情理（seem pretty reasonable to me）！

大家也可以调查该网络的第一层学习做什么。

回想卷积层分离到2块GPU上，信息不能再各层之间来回传递，因此分叉（split side）以一种真实方式断开（连接），事实证明（原来），每次运行该模型，两个分叉各司其职（specialize）。

一个分叉的神经元聚焦灰度，学习不同方向和尺寸的边缘检测；一个分叉的神经元专职处理彩色和文本，检测色比（color contrast）和模式。

记住，神经元是随机初始化的！没有人参与将神经元分为边缘检测或色比模式处理——以这种方式划分。它仅仅出现在图片分类网络。

卓越的成就（以及当时其余令人兴奋的结果）只是开始。

很快被一群改进实现的测试工作跟进并逐渐提升结果，或将该模型应用到别的领域。此外，神经网络社区，计算机视觉社区，很多项目采用卷积神经网络。

卷积神经网络是计算机视觉和现代模式识别领域的基本工具。

卷积神经网络形式化

考虑，一个一维卷积层，有着输入 ${x_n}$ 和输出 ${y_n}$ :

它相对容易表述输出和输入的关系（outputs in terms of inputs）： $$y_n=A(x_n,x_{n+1})$$

对上式举个例子： $$y_0=A(x_0,x_1)$$ $$y_1=A(x_1,x_2)$$

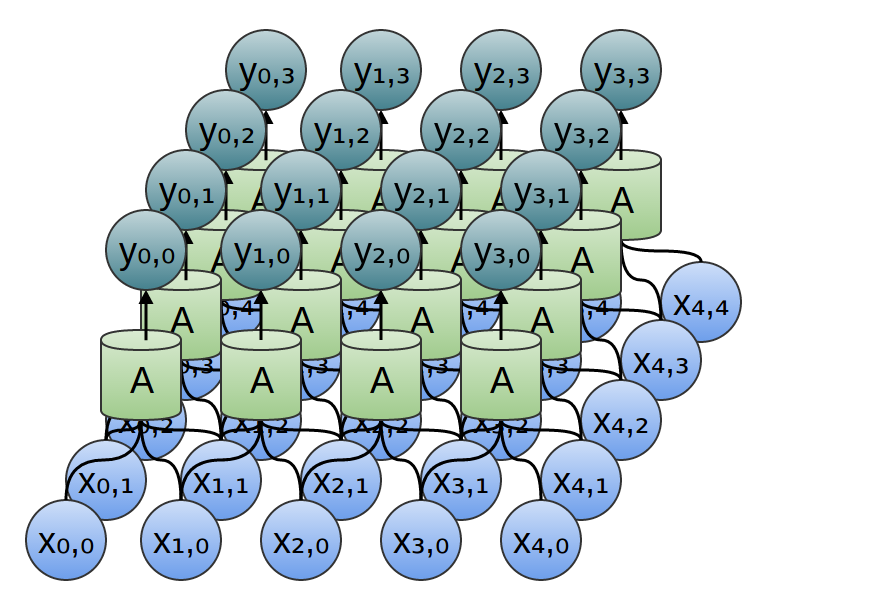
近似地，如果大家考虑一个二维卷积层，有着输入 ${x_{n,m}}$ 和输出 ${y_{n,m}}$ ：

同样，可以用如下表达是来说明输出和输入的关系： $$y_{n,m}=A\left(\begin{array}{ccc} x_{n,~m}, & x_{n+1,~m} ~\ x_{n,~m+1}, & x_{n+1,~m+1} \\end{array}\right)$$

对上式举个例子： $$y_{0,0}=A\left(\begin{array}{ccc} x_{0,~0}, & x_{1,~0}, ~\ x_{0,~1} & x_{1,~1} \\end{array}\right)$$

如果一将 $A(x)$ 写成等式： $A(x)=\sigma(Wx + b)$

则有实现一个卷积神经网络所需的一切，至少理论上是的。

实践中，这通常不是考虑卷积神经网络最好的的方法。这儿是供选择的构想，根据数学操作，叫做卷积，经常更有用！

卷积操作时一个强大的工具。在数学运算中，出现在不同背景下（come up in diverse contexts），从偏微分方程学习到概率论。部分的因其在偏微分方程的角色，卷积在物理科学是非常重要的。也在别的应用英灵扮演重要角色，例如计算机图形和信号处理。

对于大家，卷积将带来很多哦好处。

首先，卷积允许大家创建更有效地卷积层实现，相对于通俗视角（naive perspective）可能启发的思路。

其次，卷积会把公式中的杂乱去除，处理显示为 $x_i$ 的目前记账式的部分，让公式的表述不再混乱，但是这只是因为大家还没有陷入狡猾的情况。

最后，卷积将给大家提供值得注意地推理卷积层的不同视角。

老子钦佩阁下计算方法的优雅；乘真正数学之马越过计算领域一定很美，因为大家的偏好一定让步行很艰难！ —— 阿尔伯特·爱因斯坦

继续该系列的帖子

裂解卷积！

说明

本文是卷积神经网络及其一般化系列的一部分。

前两篇为熟悉深度学习的人而作，后续的可能每个人都会感兴趣。

---