forked from trekhleb/javascript-algorithms
-
Notifications
You must be signed in to change notification settings - Fork 0
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Adds Portuguese (pt-BR) translation (trekhleb#340)
* create portuguese translations * renames `Lista Ligada` to `Lista Encadeada` * revert changes on package-lock.json
- Loading branch information
1 parent
1520533
commit ed99f9d
Showing
35 changed files
with
1,111 additions
and
63 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,132 @@ | ||
| # Filtro Bloom (Bloom Filter) | ||
|
|
||
| _Leia em outro idioma:_ | ||
| [_English_](README.md) | [_Русский_](README.ru-RU.md) | ||
|
|
||
| O **bloom filter** é uma estrutura de dados probabilística | ||
| espaço-eficiente designada para testar se um elemento está | ||
| ou não presente em um conjunto de dados. Foi projetado para ser | ||
| incrivelmente rápido e utilizar o mínimo de memória ao | ||
| potencial custo de um falso-positivo. Correspondências | ||
| _falsas positivas_ são possíveis, contudo _falsos negativos_ | ||
| não são - em outras palavras, a consulta retorna | ||
| "possivelmente no conjunto" ou "definitivamente não no conjunto". | ||
|
|
||
| Bloom propôs a técnica para aplicações onde a quantidade | ||
| de entrada de dados exigiria uma alocação de memória | ||
| impraticavelmente grande se as "convencionais" técnicas | ||
| error-free hashing fossem aplicado. | ||
|
|
||
| ## Descrição do algoritmo | ||
|
|
||
| Um filtro Bloom vazio é um _bit array_ de `m` bits, todos | ||
| definidos como `0`. Também deverá haver diferentes funções | ||
| de hash `k` definidas, cada um dos quais mapeia e produz hash | ||
| para um dos elementos definidos em uma das posições `m` da | ||
| _array_, gerando uma distribuição aleatória e uniforme. | ||
| Normalmente, `k` é uma constante, muito menor do que `m`, | ||
| pelo qual é proporcional ao número de elements a ser adicionado; | ||
| a escolha precisa de `k` e a constante de proporcionalidade de `m` | ||
| são determinadas pela taxa de falsos positivos planejado do filtro. | ||
|
|
||
| Aqui está um exemplo de um filtro Bloom, representando o | ||
| conjunto `{x, y, z}`. As flechas coloridas demonstram as | ||
| posições no _bit array_ em que cada elemento é mapeado. | ||
| O elemento `w` não está definido dentro de `{x, y, z}`, | ||
| porque este produz hash para uma posição de array de bits | ||
| contendo `0`. Para esta imagem: `m = 18` e `k = 3`. | ||
|
|
||
|  | ||
|
|
||
| ## Operações | ||
|
|
||
| Existem duas operações principais que o filtro Bloom pode operar: | ||
| _inserção_ e _pesquisa_. A pesquisa pode resultar em falsos | ||
| positivos. Remoção não é possível. | ||
|
|
||
| Em outras palavras, o filtro pode receber itens. Quando | ||
| vamos verificar se um item já foi anteriormente | ||
| inserido, ele poderá nos dizer "não" ou "talvez". | ||
|
|
||
| Ambas as inserções e pesquisas são operações `O(1)`. | ||
|
|
||
| ## Criando o filtro | ||
|
|
||
| Um filtro Bloom é criado ao alocar um certo tamanho. | ||
| No nosso exemplo, nós utilizamos `100` como tamanho padrão. | ||
| Todas as posições são initializadas como `false`. | ||
|
|
||
| ### Inserção | ||
|
|
||
| Durante a inserção, um número de função hash, no nosso caso `3` | ||
| funções de hash, são utilizadas para criar hashes de uma entrada. | ||
| Estas funções de hash emitem saída de índices. A cada índice | ||
| recebido, nós simplismente trocamos o valor de nosso filtro | ||
| Bloom para `true`. | ||
|
|
||
| ### Pesquisa | ||
|
|
||
| Durante a pesquisa, a mesma função de hash é chamada | ||
| e usada para emitir hash da entrada. Depois nós checamos | ||
| se _todos_ os indices recebidos possuem o valor `true` | ||
| dentro de nosso filtro Bloom. Caso _todos_ possuam o valor | ||
| `true`, nós sabemos que o filtro Bloom pode ter tido | ||
| o valor inserido anteriormente. | ||
|
|
||
| Contudo, isto não é certeza, porque é possível que outros | ||
| valores anteriormente inseridos trocaram o valor para `true`. | ||
| Os valores não são necessariamente `true` devido ao ítem | ||
| atualmente sendo pesquisado. A certeza absoluta é impossível, | ||
| a não ser que apenas um item foi inserido anteriormente. | ||
|
|
||
| Durante a checagem do filtro Bloom para índices retornados | ||
| pela nossa função de hash, mesmo que apenas um deles possua | ||
| valor como `false`, nós definitivamente sabemos que o ítem | ||
| não foi anteriormente inserido. | ||
|
|
||
| ## Falso Positivos | ||
|
|
||
| A probabilidade de falso positivos é determinado por | ||
| três fatores: o tamanho do filtro de Bloom, o número de | ||
| funções de hash que utilizados, e o número de itens que | ||
| foram inseridos dentro do filtro. | ||
|
|
||
| A formula para calcular a probabilidade de um falso positivo é: | ||
|
|
||
| ( 1 - e <sup>-kn/m</sup> ) <sup>k</sup> | ||
|
|
||
| `k` = número de funções de hash | ||
|
|
||
| `m` = tamanho do filtro | ||
|
|
||
| `n` = número de itens inserido | ||
|
|
||
| Estas variáveis, `k`, `m` e `n`, devem ser escolhidas baseado | ||
| em quanto aceitável são os falsos positivos. Se os valores | ||
| escolhidos resultam em uma probabilidade muito alta, então | ||
| os valores devem ser ajustados e a probabilidade recalculada. | ||
|
|
||
| ## Aplicações | ||
|
|
||
| Um filtro Bloom pode ser utilizado em uma página de Blog. | ||
| Se o objetivo é mostrar aos leitores somente os artigos | ||
| em que eles nunca viram, então o filtro Bloom é perfeito | ||
| para isso. Ele pode armazenar hashes baseados nos artigos. | ||
| Depois que um usuário lê alguns artigos, eles podem ser | ||
| inseridos dentro do filtro. Na próxima vez que o usuário | ||
| visitar o Blog, aqueles artigos poderão ser filtrados (eliminados) | ||
| do resultado. | ||
|
|
||
| Alguns artigos serão inevitavelmente filtrados (eliminados) | ||
| por engano, mas o custo é aceitável. Tudo bem se um usuário nunca | ||
| ver alguns poucos artigos, desde que tenham outros novos | ||
| para ver toda vez que eles visitam o site. | ||
|
|
||
|
|
||
| ## Referências | ||
|
|
||
| - [Wikipedia](https://en.wikipedia.org/wiki/Bloom_filter) | ||
| - [Bloom Filters by Example](http://llimllib.github.io/bloomfilter-tutorial/) | ||
| - [Calculating False Positive Probability](https://hur.st/bloomfilter/?n=4&p=&m=18&k=3) | ||
| - [Bloom Filters on Medium](https://blog.medium.com/what-are-bloom-filters-1ec2a50c68ff) | ||
| - [Bloom Filters on YouTube](https://www.youtube.com/watch?v=bEmBh1HtYrw) |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,32 @@ | ||
| # Conjunto Disjuntor (Disjoint Set) | ||
|
|
||
| _Leia em outro idioma:_ | ||
| [_English_](README.md) | [_Русский_](README.ru-RU.md) | ||
|
|
||
| **Conjunto Disjuntor** | ||
|
|
||
| **Conjunto Disjuntor** é uma estrutura de dados (também chamado de | ||
| estrutura de dados de union–find ou merge–find) é uma estrutura de dados | ||
| que rastreia um conjunto de elementos particionados em um número de | ||
| subconjuntos separados (sem sobreposição). | ||
| Ele fornece operações de tempo quase constante (limitadas pela função | ||
| inversa de Ackermann) para *adicionar novos conjuntos*, para | ||
| *mesclar/fundir conjuntos existentes* e para *determinar se os elementos | ||
| estão no mesmo conjunto*. | ||
| Além de muitos outros usos (veja a seção Applications), conjunto disjuntor | ||
| desempenham um papel fundamental no algoritmo de Kruskal para encontrar a | ||
| árvore geradora mínima de um gráfico (graph). | ||
|
|
||
|
|
||
|  | ||
|
|
||
| *MakeSet* cria 8 singletons. | ||
|
|
||
|  | ||
|
|
||
| Depois de algumas operações de *Uniões*, alguns conjuntos são agrupados juntos. | ||
|
|
||
| ## Referências | ||
|
|
||
| - [Wikipedia](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) | ||
| - [By Abdul Bari on YouTube](https://www.youtube.com/watch?v=wU6udHRIkcc&index=14&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,114 @@ | ||
| # Lista Duplamente Ligada (Doubly Linked List) | ||
|
|
||
| _Leia em outro idioma:_ | ||
| [_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | ||
|
|
||
| Na ciência da computação, uma **lista duplamente conectada** é uma estrutura | ||
| de dados vinculada que se consistem em um conjunto de registros | ||
| sequencialmente vinculados chamados de nós (nodes). Em cada nó contém dois | ||
| campos, chamados de ligações, que são referenciados ao nó anterior e posterior | ||
| de uma sequência de nós. O começo e o fim dos nós anteriormente e posteiormente | ||
| ligados, respectiviamente, apontam para algum tipo de terminação, normalmente | ||
| um nó sentinela ou nulo, para facilitar a travessia da lista. Se existe | ||
| somente um nó sentinela, então a lista é ligada circularmente através do nó | ||
| sentinela. Ela pode ser conceitualizada como duas listas individualmente ligadas | ||
| e formadas a partir dos mesmos itens, mas em ordem sequencial opostas. | ||
|
|
||
|  | ||
|
|
||
| Os dois nós ligados permitem a travessia da lista em qualquer direção. | ||
| Enquanto adicionar ou remover um nó de uma lista duplamente vinculada requer | ||
| alterar mais ligações (conexões) do que em uma lista encadeada individualmente | ||
| (singly linked list), as operações são mais simples e potencialmente mais | ||
| eficientes (para nós que não sejam nós iniciais) porque não há necessidade | ||
| de se manter rastreamento do nó anterior durante a travessia ou não há | ||
| necessidade de percorrer a lista para encontrar o nó anterior, para que | ||
| então sua ligação/conexão possa ser modificada. | ||
|
|
||
| ## Pseudocódigo para Operações Básicas | ||
|
|
||
| ### Inserir | ||
|
|
||
| ```text | ||
| Add(value) | ||
| Pre: value is the value to add to the list | ||
| Post: value has been placed at the tail of the list | ||
| n ← node(value) | ||
| if head = ø | ||
| head ← n | ||
| tail ← n | ||
| else | ||
| n.previous ← tail | ||
| tail.next ← n | ||
| tail ← n | ||
| end if | ||
| end Add | ||
| ``` | ||
|
|
||
| ### Deletar | ||
|
|
||
| ```text | ||
| Remove(head, value) | ||
| Pre: head is the head node in the list | ||
| value is the value to remove from the list | ||
| Post: value is removed from the list, true; otherwise false | ||
| if head = ø | ||
| return false | ||
| end if | ||
| if value = head.value | ||
| if head = tail | ||
| head ← ø | ||
| tail ← ø | ||
| else | ||
| head ← head.next | ||
| head.previous ← ø | ||
| end if | ||
| return true | ||
| end if | ||
| n ← head.next | ||
| while n = ø and value !== n.value | ||
| n ← n.next | ||
| end while | ||
| if n = tail | ||
| tail ← tail.previous | ||
| tail.next ← ø | ||
| return true | ||
| else if n = ø | ||
| n.previous.next ← n.next | ||
| n.next.previous ← n.previous | ||
| return true | ||
| end if | ||
| return false | ||
| end Remove | ||
| ``` | ||
|
|
||
| ### Travessia reversa | ||
|
|
||
| ```text | ||
| ReverseTraversal(tail) | ||
| Pre: tail is the node of the list to traverse | ||
| Post: the list has been traversed in reverse order | ||
| n ← tail | ||
| while n = ø | ||
| yield n.value | ||
| n ← n.previous | ||
| end while | ||
| end Reverse Traversal | ||
| ``` | ||
|
|
||
| ## Complexidades | ||
|
|
||
| ## Complexidade de Tempo | ||
|
|
||
| | Acesso | Pesquisa | Inserção | Remoção | | ||
| | :-------: | :---------: | :------: | :------: | | ||
| | O(n) | O(n) | O(1) | O(n) | | ||
|
|
||
| ### Complexidade de Espaço | ||
|
|
||
| O(n) | ||
|
|
||
| ## Referências | ||
|
|
||
| - [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list) | ||
| - [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,29 @@ | ||
| # Gráfico (Graph) | ||
|
|
||
| _Read this in other languages:_ | ||
| [_English_](README.md) | [_简体中文_](README.zh-CN.md) | [_Русский_](README.ru-RU.md) | ||
|
|
||
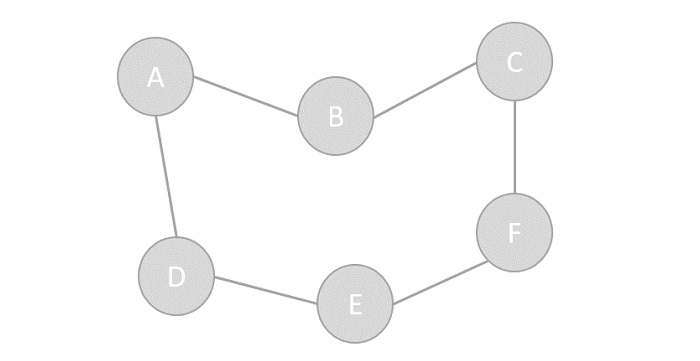
| Na ciência da computação, um **gráfico** é uma abstração de estrutura | ||
| de dados que se destina a implementar os conceitos da matemática de | ||
| gráficos direcionados e não direcionados, especificamente o campo da | ||
| teoria dos gráficos. | ||
|
|
||
| Uma estrutura de dados gráficos consiste em um finito (e possivelmente | ||
| mutável) conjunto de vértices, nós ou pontos, juntos com um | ||
| conjunto de pares não ordenados desses vértices para um gráfico não | ||
| direcionado ou para um conjunto de pares ordenados para um gráfico | ||
| direcionado. Esses pares são conhecidos como arestas, arcos | ||
| ou linhas diretas para um gráfico não direcionado e como setas, | ||
| arestas direcionadas, arcos direcionados ou linhas direcionadas | ||
| para um gráfico direcionado. | ||
|
|
||
| Os vértices podem fazer parte a estrutura do gráfico, ou podem | ||
| ser entidades externas representadas por índices inteiros ou referências. | ||
|
|
||
|  | ||
|
|
||
| ## Referências | ||
|
|
||
| - [Wikipedia](https://en.wikipedia.org/wiki/Graph_(abstract_data_type)) | ||
| - [Introduction to Graphs on YouTube](https://www.youtube.com/watch?v=gXgEDyodOJU&index=9&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) | ||
| - [Graphs representation on YouTube](https://www.youtube.com/watch?v=k1wraWzqtvQ&index=10&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) |
Oops, something went wrong.