A Java implementation of Locality Sensitive Hashing (LSH).
Locality Sensitive Hashing (LSH) is a family of hashing methods that tent to produce the same hash (or signature) for similar items. There exist different LSH functions, that each correspond to a similarity metric. For example, the MinHash algorithm is designed for Jaccard similarity (the relative number of elements that two sets have in common). For cosine similarity, the traditional LSH algorithm used is Random Projection, but others exist, like Super-Bit, that deliver better resutls.
LSH functions have two main use cases:
- Compute the signature of large input vectors. These signatures can be used to quickly estimate the similarity between vectors.
- With a given number of buckets, bin similar vectors together.
This library implements Locality Sensitive Hashing (LSH), as described in Leskovec, Rajaraman & Ullman (2014), "Mining of Massive Datasets", Cambridge University Press.
Are currently implemented:
- MinHash algorithm for Jaccard index;
- Super-Bit algorithm for cosine similarity.
The coeficients of hashing functions are randomly choosen when the LSH object is instantiated. You can thus only compare signatures or bucket binning generated by the same LSH object. To reuse your LSH object between executions, you have to serialize it and save it to a file (see below the example of LSH object serialization).
##Download
Using maven:
<dependency>
<groupId>info.debatty</groupId>
<artifactId>java-lsh</artifactId>
<version>RELEASE</version>
</dependency>
Or see the releases page.
##MinHash
MinHash is a hashing scheme that tents to produce similar signatures for sets that have a high Jaccard similarity.
The Jaccard similarity between two sets is the relative number of elements these sets have in common: J(A, B) = |A ∩ B| / |A ∪ B| A MinHash signature is a sequence of numbers produced by multiple hash functions hi. It can be shown that the Jaccard similarity between two sets is also the probability that this hash result is the same for the two sets: J(A, B) = Pr[hi(A) = hi(B)]. Therefore, MinHash signatures can be used to estimate Jaccard similarity between two sets. Moreover, it can be shown that the expected estimation error is O(1 / sqrt(n)), where n is the size of the signature (the number of hash functions that are used to produce the signature).
import info.debatty.java.lsh.LSHMinHash;
import java.util.Random;
public class SimpleLSHMinHashExample {
public static void main(String[] args) {
// proportion of 0's in the vectors
// if the vectors are dense (lots of 1's), the average jaccard similarity
// will be very high (especially for large vectors), and LSH
// won't be able to distinguish them
// as a result, all vectors will be binned in the same bucket...
double sparsity = 0.75;
// Number of sets
int count = 10000;
// Size of vectors
int n = 100;
// LSH parameters
// the number of stages is also sometimes called thge number of bands
int stages = 2;
// Attention: to get relevant results, the number of elements per bucket
// should be at least 100
int buckets = 10;
// Let's generate some random sets
boolean[][] vectors = new boolean[count][n];
Random rand = new Random();
for (int i = 0; i < count; i++) {
for (int j = 0; j < n; j++) {
vectors[i][j] = rand.nextDouble() > sparsity;
}
}
// Create and configure LSH algorithm
LSHMinHash lsh = new LSHMinHash(stages, buckets, n);
int[][] counts = new int[stages][buckets];
// Perform hashing
for (boolean[] vector : vectors) {
int[] hash = lsh.hash(vector);
for (int i = 0; i < hash.length; i++) {
counts[i][hash[i]]++;
}
print(vector);
System.out.print(" : ");
print(hash);
System.out.print("\n");
}
System.out.println("Number of elements per bucket at each stage:");
for (int i = 0; i < stages; i++) {
print(counts[i]);
System.out.print("\n");
}
}
static void print(int[] array) {
System.out.print("[");
for (int v : array) {
System.out.print("" + v + " ");
}
System.out.print("]");
}
static void print(boolean[] array) {
System.out.print("[");
for (boolean v : array) {
System.out.print(v ? "1" : "0");
}
System.out.print("]");
}
}Pay attention, LSH using MinHash is very sensitive to the average Jaccard similarity in your dataset! If most vectors in your dataset have a Jaccard similarity above or below 0.5, they might all fall in the same bucket. This is illustrated by example below:
import info.debatty.java.lsh.LSHMinHash;
import info.debatty.java.lsh.MinHash;
import java.util.Random;
public class LSHMinHashExample {
public static void main(String[] args) {
// Number of sets
int count = 2000;
// Size of dictionary
int n = 100;
// Number of buckets
// Attention: to get relevant results, the number of elements per bucket
// should be at least 100
int buckets = 10;
// Let's generate some random sets
boolean[][] vectors = new boolean[count][];
Random r = new Random();
// To get some interesting measures, we first generate a single
// sparse random vector
vectors[0] = new boolean[n];
for (int j = 0; j < n; j++) {
vectors[0][j] = (r.nextInt(10) == 0);
}
// Then we generate the other vectors, which have a reasonable chance
// to look like the first one...
for (int i = 1; i < count; i++) {
vectors[i] = new boolean[n];
for (int j = 0; j < n; j++) {
vectors[i][j] = (r.nextDouble() <= 0.7 ? vectors[0][j] : (r.nextInt(10) == 0));
}
}
// Now we can proceed to LSH binning
// We will test multiple stages
for (int stages = 1; stages <= 10; stages++) {
// Compute the LSH hash of each vector
LSHMinHash lsh = new LSHMinHash(stages, buckets, n);
int[][] hashes = new int[count][];
for (int i = 0; i < count; i++) {
boolean[] vector = vectors[i];
hashes[i] = lsh.hash(vector);
}
// We now have the LSH hash for each input set
// Let's have a look at how similar sets (according to Jaccard
// index) were binned...
int[][] results = new int[11][2];
for (int i = 0; i < vectors.length; i++) {
boolean[] vector1 = vectors[i];
int[] hash1 = hashes[i];
for (int j = 0; j < i; j++) {
boolean[] vector2 = vectors[j];
int[] hash2 = hashes[j];
// We compute the similarity between each pair of sets
double similarity = MinHash.jaccardIndex(vector1, vector2);
// We count the number of pairs with similarity 0.1, 0.2,
// 0.3, etc.
results[(int) (10 * similarity)][0]++;
// Do they fall in the same bucket for one of the stages?
for (int stage = 0; stage < stages; stage++) {
if (hash1[stage] == hash2[stage]) {
results[(int) (10 * similarity)][1]++;
break;
}
}
}
}
// Now we can display (and plot in Gnuplot) the result:
// For pairs that have a similarity x, the probability of falling
// in the same bucket for at least one of the stages is y
for (int i = 0; i < results.length; i++) {
double similarity = (double) i / 10;
double probability = 0;
if (results[i][0] != 0) {
probability = (double) results[i][1] / results[i][0];
}
System.out.println("" + similarity + "\t" + probability + "\t" + stages);
}
// Separate the series for Gnuplot...
System.out.print("\n");
}
}
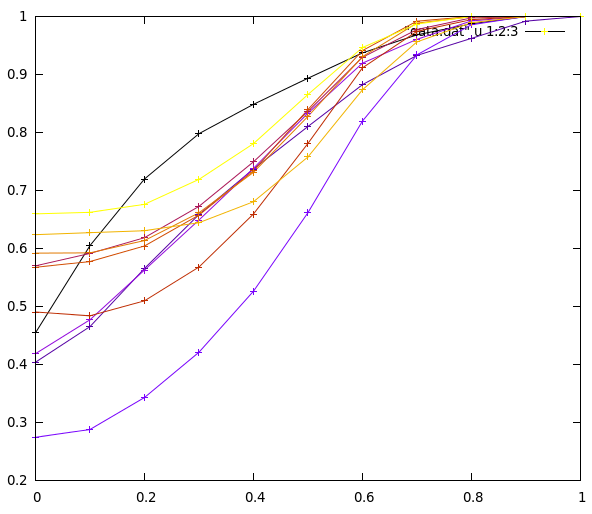
}This example will run LSH binning for different number of stages. At each step, for each value of Jaccard similarity between pairs of sets (in the range [0, 0.1, 0.2, ... 1.0]), the program computes the probability that these two pairs fall in the same bucket for at least one stage. The results can be plotted with Gnuplot for example:
On this figure, the x-axis is the Jaccard similarity between sets, the y-axis is the probability that these pairs fall in the same bucket for at least one stage. The different series represent different values for the number of stages (from 1 to 10).
We can clearly recognize the typical S curve of MinHash, with the threshold (the point where the curve is the steepest) located around x = 0.5.
This curve is very important! It shows that if all your sets are similar (similarity above 0.6), all sets will most probably fall in a single bucket. And all other buckets will thus most probably be empty. This can happen for example if your dataset is skewed and presents some sort of principal direction.
At the opposite, if your sets are all different from each other (similarity below 0.2), the curve is nearly flat. This means that pairs of sets have the same probability of falling in the same bucket, independantly of their similarity. The items are then randomly binned into the buckets. If using B buckets and S stages, computing the probability that two items are binned in the same bucket is similar to the problem of rolling S times a dice with B values. The resuling probability is 1 - [(B-1) / B]^S. The computed probability for 10 buckets is presented in table below, and roughly correspond to the above graph.
| Stages | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Pr | 0.1 | 0.19 | 0.27 | 0.34 | 0.41 | 0.47 | 0.52 | 0.57 | 0.61 | 0.65 |
If you simply wish to compute MinHash signatures (witout performing LSH binning), you can directly use the MinHash class:
import info.debatty.java.lsh.MinHash;
import java.util.TreeSet;
public class MinHashExample {
public static void main(String[] args) {
// Initialize the hash function for an similarity error of 0.1
// For sets built from a dictionary of 5 items
MinHash minhash = new MinHash(0.1, 5);
// Sets can be defined as an vector of booleans:
// [1 0 0 1 0]
boolean[] vector1 = {true, false, false, true, false};
int[] sig1 = minhash.signature(vector1);
// Or as a set of integers:
// set2 = [1 0 1 1 0]
TreeSet<Integer> set2 = new TreeSet<Integer>();
set2.add(0);
set2.add(2);
set2.add(3);
int[] sig2 = minhash.signature(set2);
System.out.println("Signature similarity: " + minhash.similarity(sig1, sig2));
System.out.println("Real similarity (Jaccard index)" +
MinHash.JaccardIndex(MinHash.Convert2Set(vector1), set2));
}
}Which will produce:
Signature similarity: 0.6767676767676768
Real similarity (Jaccard index)0.6666666666666666
##Super-Bit
Super-Bit is an improvement of Random Projection LSH. It computes an estimation of cosine similarity. In Super-Bit, the K random vectors are orthogonalized in L batches of N vectors, where
- N is called the Super-Bit depth
- L is called the number of Super-Bits
- K = L * N is the code length (the size of the signature)
Super-Bit Locality-Sensitive Hashing, Jianqiu Ji, Jianmin Li, Shuicheng Yan, Bo Zhang, Qi Tian http://papers.nips.cc/paper/4847-super-bit-locality-sensitive-hashing.pdf Published in Advances in Neural Information Processing Systems 25, 2012
The cosine similarity between two points vectors in R^n is the cosine of their angle. It is computed as v1 . v2 / (|v1| * |v2|). Two vectors with the same orientation have a Cosine similarity of 1, two vectors at 90° have a similarity of 0, and two vectors diametrically opposed have a similarity of -1, independent of their magnitude.
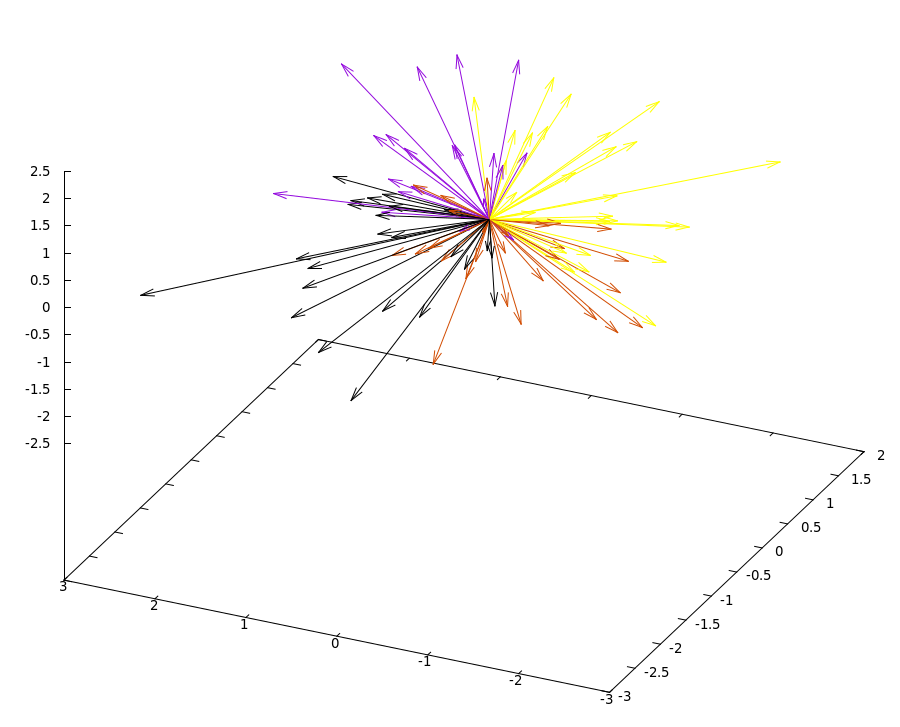
Here is an example of how to quickly bin together vectors that have a high cosine similarity using LSH + Super-Bit:
import info.debatty.java.lsh.LSHSuperBit;
import java.util.Random;
public class LSHSuperBitExample {
public static void main(String[] args) {
int count = 100;
// R^n
int n = 3;
int stages = 2;
int buckets = 4;
// Produce some vectors in R^n
Random r = new Random();
double[][] vectors = new double[count][];
for (int i = 0; i < count; i++) {
vectors[i] = new double[n];
for (int j = 0; j < n; j++) {
vectors[i][j] = r.nextGaussian();
}
}
LSHSuperBit lsh = new LSHSuperBit(stages, buckets, n);
// Compute a SuperBit signature, and a LSH hash
for (int i = 0; i < count; i++) {
double[] vector = vectors[i];
int[] hash = lsh.hash(vector);
for (double v : vector) {
System.out.printf("%6.2f\t", v);
}
System.out.print(hash[0]);
System.out.print("\n");
}
}
}This will produce something like, where the last column is the bucket in which this vector was binned (at first stage):
-0.48 -0.68 1.87 1
0.77 0.11 2.20 1
-0.05 0.23 -1.12 2
1.30 0.02 1.44 3
-0.34 -1.51 0.78 3
1.64 0.02 0.84 3
-0.74 1.58 -0.79 0
-0.17 -1.27 -1.25 2
...
This can be plotted with Gnuplot for example:
If you only wish to compute super-bit signatures of vectors (without performing LSH binning), you can directly use the SuperBit class:
import info.debatty.lsh.SuperBit;
public class MyApp {
public static void main(String[] args) {
int n = 10;
// Initialize Super-Bit
SuperBit sb = new SuperBit(n);
Random rand = new Random();
double[] v1 = new double[n];
double[] v2 = new double[n];
for (int i = 0; i < n; i++) {
v1[i] = rand.nextInt();
v2[i] = rand.nextInt();
}
boolean[] sig1 = sb.signature(v1);
boolean[] sig2 = sb.signature(v2);
System.out.println("Signature (estimated) similarity: " + sb.similarity(sig1, sig2));
System.out.println("Real (cosine) similarity: " + cosineSimilarity(v1, v2));
}As the parameters of the hashing function are randomly initialized when the LSH object is instantiated:
- two LSH objects will produce different hashes and signatures for the same input vector;
- two executions of your program will produce different hashes and signatures for the same input vector;
- the signatures produced by two different LSH objects can not be used to estimate the similarity between vectors.
There are two possibilities to produce comparable signatures: provide an initial seed or serialize your hash object.
import info.debatty.java.lsh.MinHash;
import java.util.Random;
public class InitialSeed {
public static void main(String[] args) {
// Initialize two minhash objects, with the same seed
int signature_size = 20;
int dictionary_size = 100;
long initial_seed = 123456;
MinHash mh = new MinHash(signature_size, dictionary_size, initial_seed);
MinHash mh2 = new MinHash(signature_size, dictionary_size, initial_seed);
// Create a single vector of size dictionary_size
Random r = new Random();
boolean[] vector = new boolean[dictionary_size];
for (int i = 0; i < dictionary_size; i++) {
vector[i] = r.nextBoolean();
}
// The two minhash objects will produce the same signature
println(mh.signature(vector));
println(mh2.signature(vector));
}
static void println(final int[] array) {
System.out.print("[");
for (int v : array) {
System.out.print("" + v + " ");
}
System.out.println("]");
}
}Will output:
[0 0 1 1 3 3 0 1 0 2 0 0 9 1 0 0 0 1 7 0 ]
[0 0 1 1 3 3 0 1 0 2 0 0 9 1 0 0 0 1 7 0 ]
import info.debatty.java.lsh.LSHMinHash;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.ObjectInputStream;
import java.io.ObjectOutputStream;
import java.util.Random;
public class SerializeExample {
public static void main(String[] args)
throws IOException, ClassNotFoundException {
// Create a single random boolean vector
int n = 100;
double sparsity = 0.75;
boolean[] vector = new boolean[n];
Random rand = new Random();
for (int j = 0; j < n; j++) {
vector[j] = rand.nextDouble() > sparsity;
}
// Create and configure LSH
int stages = 2;
int buckets = 10;
LSHMinHash lsh = new LSHMinHash(stages, buckets, n);
println(lsh.hash(vector));
// Create another LSH object
// as the parameters of the hashing function are randomly initialized
// these two LSH objects will produce different hashes for the same
// input vector!
LSHMinHash other_lsh = new LSHMinHash(stages, buckets, n);
println(other_lsh.hash(vector));
// Moreover, signatures produced by different LSH objects cannot
// be used to compute estimated similarity!
// The solution is to serialize and save the object, so it can be
// reused later...
File tempfile = File.createTempFile("lshobject", ".ser");
FileOutputStream fout = new FileOutputStream(tempfile);
ObjectOutputStream oos = new ObjectOutputStream(fout);
oos.writeObject(lsh);
oos.close();
System.out.println(
"LSH object serialized to " + tempfile.getAbsolutePath());
FileInputStream fin = new FileInputStream(tempfile);
ObjectInputStream ois = new ObjectInputStream(fin);
LSHMinHash saved_lsh = (LSHMinHash) ois.readObject();
println(saved_lsh.hash(vector));
}
static void println(int[] array) {
System.out.print("[");
for (int v : array) {
System.out.print("" + v + " ");
}
System.out.println("]");
}
}Will produce something like:
[5 5 ]
[3 1 ]
LSH object serialized to /tmp/lshobject5903174677942358274.ser
[5 5 ]