Time series symbolic discretization (approximation) with SAX

This code is released under GPL v.2.0 and implements in Java:

• Symbolic Aggregate approXimation (i.e., SAX) toolkit stack [1]
• EMMA (Enumeration of Motifs through Matrix Approximation) algorithm for time series motif discovery [2]
• HOT-SAX - a time series anomaly (discord) discovery algorithm [3]
• time series bitmap-related routines [4]

Note that the most of library's functionality is also available in R and Python as well...

[1] Lin, J., Keogh, E., Patel, P., and Lonardi, S., Finding Motifs in Time Series, The 2nd Workshop on Temporal Data Mining, the 8th ACM Int'l Conference on KDD (2002)

[2] Patel, P., Keogh, E., Lin, J., Lonardi, S., Mining Motifs in Massive Time Series Databases, In Proc. ICDM (2002)

[3] Keogh, E., Lin, J., Fu, A., HOT SAX: Efficiently finding the most unusual time series subsequence, In Proc. ICDM (2005)

[4] Kumar, N., Lolla, V.N., Keogh, E.J., Lonardi, S. and Chotirat (Ann) Ratanamahatana, Time-series Bitmaps: a Practical Visualization Tool for Working with Large Time Series Databases, In SDM 2005 Apr 21 (pp. 531-535).

Citing this work:

If you are using this implementation for you academic work, please cite our Grammarviz 3.0 paper:

[Citation] Senin, P., Lin, J., Wang, X., Oates, T., Gandhi, S., Boedihardjo, A.P., Chen, C., Frankenstein, S., GrammarViz 3.0: Interactive Discovery of Variable-Length Time Series Patterns, ACM Trans. Knowl. Discov. Data, February 2018.

an alternative solution for recurrent and anomalous patterns detection:

If you are interested in more advance techniques for time series pattern discovery -- the one which allows to discover recurrent and anomalous patterns of variable length -- please check out our new tool called GrammarViz 2.0. Based on symbolic discretization, Grammatical Inference, and algorithmic (i.e., Kolmogorv complexity) this new approach facilitates linear-time variable length motifs discovery and orders of magnitude faster than HOT-SAX discords discovery (but exactness is not guaranteed).

0.0 SAX transform in a nutshell

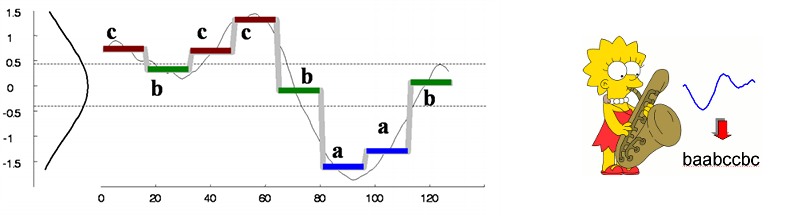
SAX is used to transform a sequence of rational numbers (i.e., a time series) into a sequence of letters (i.e., a string). An illustration of a time series of 128 points converted into the word of 8 letters:

As discretization is probably the most used transformation in data mining, SAX has been widely used throughout the field. Find more information about SAX at its authors pages: SAX overview by Jessica Lin, Eamonn Keogh's SAX page, or at sax-vsm wiki page.

1.0 Building

The code is written in Java and I use maven to build it. Use the profile single to build an executable jar containing all the dependencies:

$ mvn package -P single

[INFO] Scanning for projects...
[INFO] ------------------------------------------------------------------------
[INFO] Building jmotif-sax
[INFO]    task-segment: [package]

...

[INFO] Building jar: /media/Stock/git/jmotif-sax/target/jmotif-sax-1.0.1-SNAPSHOT-jar-with-dependencies.jar
[INFO] ------------------------------------------------------------------------
[INFO] BUILD SUCCESSFUL

2.0 Time series to SAX conversion using CLI

The jar file can be used to convert a time series (represented as a single-column text file) to SAX via sliding window in command line:

$ java -jar target/jmotif-sax-0.1.1-SNAPSHOT-jar-with-dependencies.jar
Usage: <main class> [options] 
Options:
		--alphabet_size, -a
		   SAX alphabet size, Default: 3
		--data, -d
		   The input file name
		--out, -o
   		   The output file name
		--strategy
   		   SAX numerosity reduction strategy
   		   Default: EXACT, Possible Values: [NONE, EXACT, MINDIST]
		--threads, -t
   		   number of threads to use, Default: 1
		--threshold
   		   SAX normalization threshold, Default: 0.01
		--window_size, -w
   		   SAX sliding window size, Default: 30
		--word_size, -p
   		   SAX PAA word size, Default: 4

When run, it prints the time series point index and a corresponding word:

$ java -jar "target/jmotif-sax-1.0.1-SNAPSHOT-jar-with-dependencies.jar" \ 
                      -d src/resources/test-data/ecg0606_1.csv -o test.txt
$ head test.txt
0, aabc
8, aacc
13, abcc
20, abcb
...

3.0 API usage

There two classes implementing end-to-end workflow for SAX. These are TSProcessor (implements time series-related functions) and SAXProcessor (implements the discretization). Below are typical use scenarios:

3.1 Discretizing time-series by chunking:

// instantiate classes
NormalAlphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// read the input file
double[] ts = TSProcessor.readFileColumn(dataFName, 0, 0);

// perform the discretization
String str = sp.ts2saxByChunking(ts, paaSize, na.getCuts(alphabetSize), nThreshold);

// print the output
System.out.println(str);

3.2 Discretizing time-series via sliding window:

// instantiate classes
NormalAlphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// read the input file
double[] ts = TSProcessor.readFileColumn(dataFName, 0, 0);

// perform the discretization
SAXRecords res = sp.ts2saxViaWindow(ts, slidingWindowSize, paaSize, 
	na.getCuts(alphabetSize), nrStrategy, nThreshold);

// print the output
Set<Integer> index = res.getIndexes();
for (Integer idx : index) {
	System.out.println(idx + ", " + String.valueOf(res.getByIndex(idx).getPayload()));
}

3.3 Multi-threaded discretization via sliding window:

// instantiate classes
NormalAlphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// read the input file
double[] ts = TSProcessor.readFileColumn(dataFName, 0, 0);

// perform the discretization using 8 threads
ParallelSAXImplementation ps = new ParallelSAXImplementation();
SAXRecords res = ps.process(ts, 8, slidingWindowSize, paaSize, alphabetSize, 
	nrStrategy, nThreshold);

// print the output
Set<Integer> index = res.getIndexes();
for (Integer idx : index) {
	System.out.println(idx + ", " + String.valueOf(res.getByIndex(idx).getPayload()));
}

3.4 Time series motif (recurrent pattern) discovery

Class EMMAImplementation implements a method for getting the most frequent structural patterns with EMMA algorithm:

// read the data
double[] series = TSProcessor.readFileColumn(DATA_FNAME, 0, 0);

// find the best motif with EMMA
MotifRecord motifsEMMA = EMMAImplementation.series2EMMAMotifs(series, MOTIF_SIZE, 
				MOTIF_RANGE, PAA_SIZE, ALPHABET_SIZE, ZNORM_THRESHOLD);
    		
// print motifs
System.out.println(motifsEMMA);

Class SAXRecords implements a method for getting the most frequent SAX words:

// read the data
double[] series = TSProcessor.readFileColumn(DATA_FNAME, 0, 0);

// instantiate classes
Alphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// perform discretization
saxData = sp.ts2saxViaWindow(series, WIN_SIZE, PAA_SIZE, na.getCuts(ALPHABET_SIZE),
    		NR_STRATEGY, NORM_THRESHOLD);
    		
// get the list of 10 most frequent SAX words
ArrayList<SAXRecord> motifs = saxData.getMotifs(10);
SAXRecord topMotif = motifs.get(0);
    
// print motifs
System.out.println("top motif " + String.valueOf(topMotif.getPayload()) + " seen " + 
	   		topMotif.getIndexes().size() + " times.");

3.5 Time series anomaly detection using brute-force search

The BruteForceDiscordImplementation class implements a brute-force search for discords, which is intended to be used as a reference in tests (HOTSAX and NONE yield exactly the same discords).

discordsBruteForce = BruteForceDiscordImplementation.series2BruteForceDiscords(series, 
   WIN_SIZE, DISCORDS_TO_TEST, new LargeWindowAlgorithm());
    
    for (DiscordRecord d : discordsBruteForce) {
       System.out.println("brute force discord " + d.toString());
    }

3.6 Time series anomaly (discord) discovery using HOTSAX

The HOTSAXImplementation class implements a HOTSAX algorithm for time series discord discovery:

  discordsHOTSAX = HOTSAXImplementation.series2Discords(series, DISCORDS_TO_TEST, WIN_SIZE,
      PAA_SIZE, ALPHABET_SIZE, STRATEGY, NORM_THRESHOLD);
      
  for (DiscordRecord d : discordsHOTSAX) {
    System.out.println("hotsax hash discord " + d.toString());
  }

Note, that the "proper" strategy to use with HOTSAX is NumerosityReductionStrategy.NONE but you may try others in order to speed-up the search, exactness however, is not guaranteed.

The library source code has examples (tests) for using these here and here.

4.0 Time series bitmap

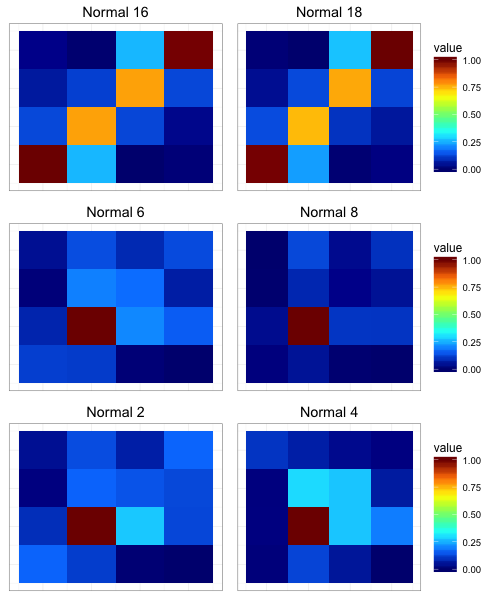
The library also implements simple routines to convert a time series to bitmap following [4]. Here is an example of six datasets from the paper:

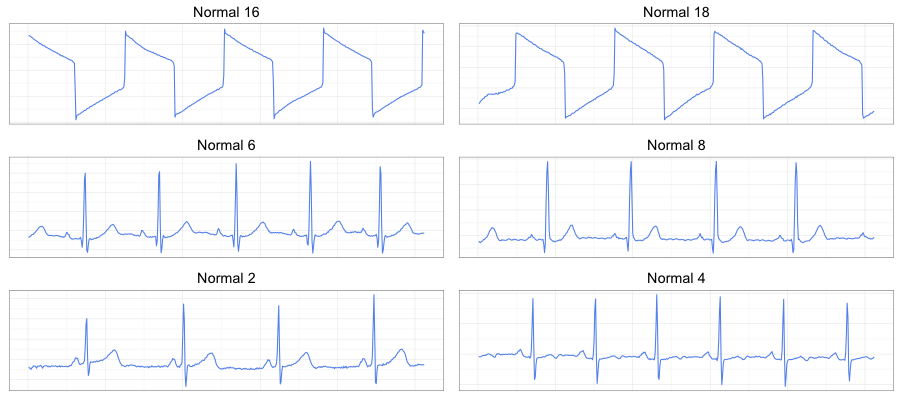
which were converted into the digram frequencies tables and colored with Jet palette:

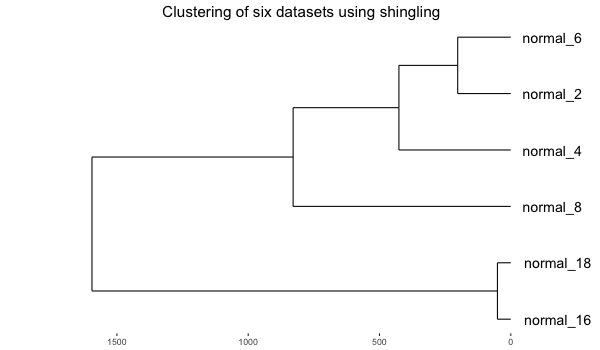
and then clustered (hc, ave) based on the digram occurrence frequencies (euclidean):

5.0 Threaded performance

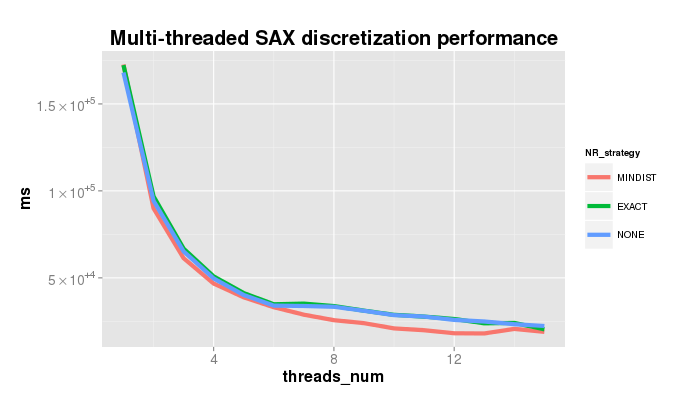
The plot shows the speedup achieved when using the parallelized SAX version on the dataset 300_signal1.txt of length 536,976 points. Parameters used in the experiment: sliding window size 200, PAA size 11, alphabet size 7, and three different NR strategies.

Note, that for MINDIST numerosity reduction strategy the parallelized code performs NONE-based discretization first and prunes the result second. The difference in performance for 7+ CPUs on the plot below is due to the uneven server load, I guess.

Made with Aloha!

Versions:

1.1.4

• fixing EMMA for a case of "tie" -- chosing a motif with the smallest variance

1.1.3

• adding an EMMA implementation with a fake ADM
• some old code optimization (breaking some APIs)

1.1.2

• maintenance release -- most of changes in the shingling routines, fitting its API for other projects

1.1.1

• HOTSAX implementation parameters bug fix

1.1.0

• zNormalization behavior for a case when SD is less than threshold is changed -- yields zeros
• GrammarViz3.0 release

1.0.10

• shingling/bitmap CLI fixes
• SAX via chunking fixes -- proper symbol indexes computed (thanks s-mckay!)

1.0.9

• fixed the error with the discord size computation
• changed HOTSAX and BRUTEFORCE behavior by adding z-Normalization to the distance computation routine

1.0.8

• added shingling

1.0.7

• logback dependencies removed

1.0.5 - 1.0.6

• added discretization approximation error computation for grammarviz3 work

1.0.4

• fixed SAX transform via sliding window, last window is now added

1.0.3

• improved PAA performance

1.0.1 - 1.0.2

• more tests, bug fixes, CI

0.0.1 - 1.0.0

• cleaning up the old JMotif code and decoupling the SAX code from the rest