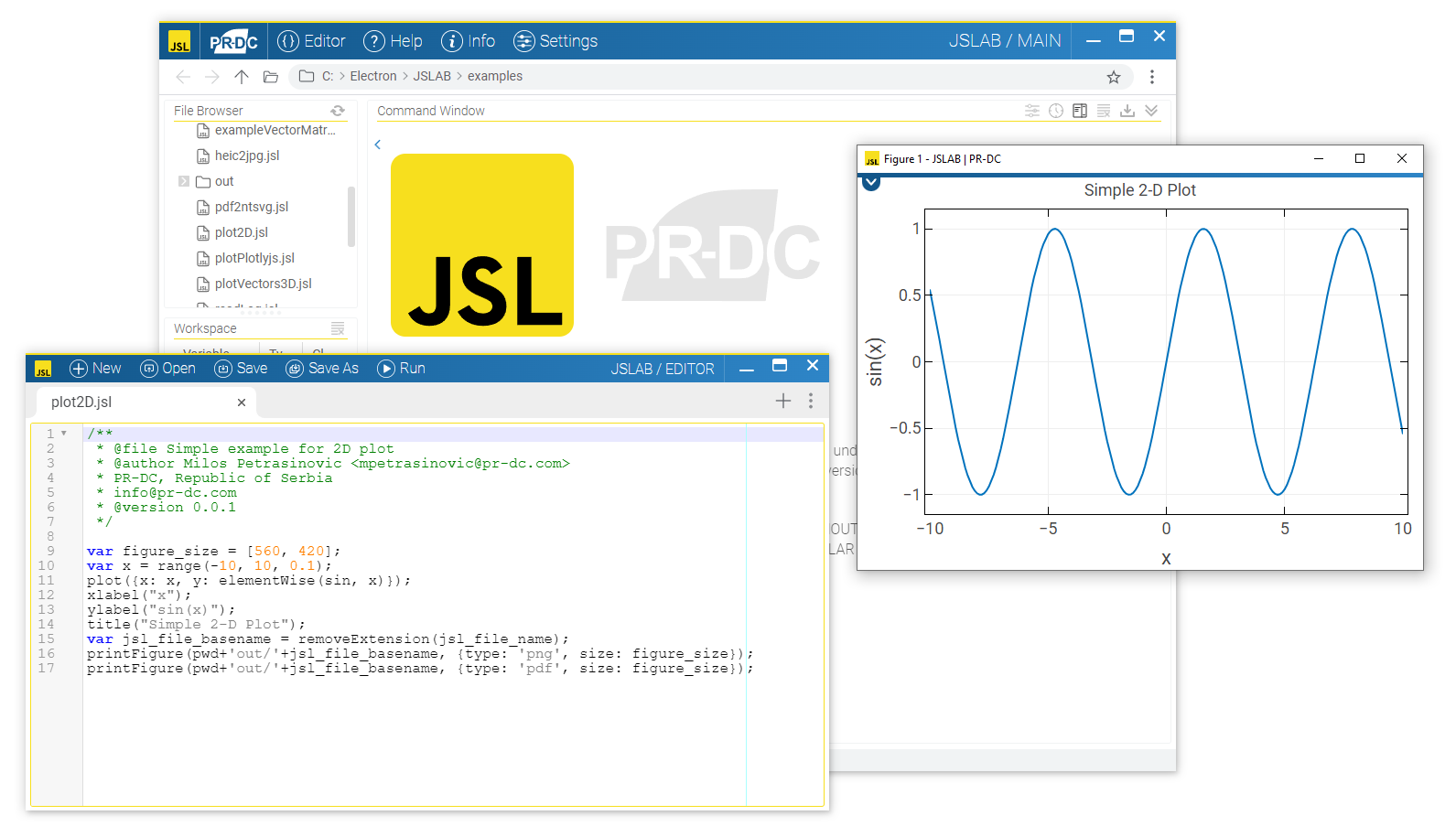
The JavaScript Laboratory (JSLAB) is an open-source environment designed for scientific computing, data visualization, and various other computer operations. Inspired by GNU Octave and Matlab, JSLAB leverages the advantages of JavaScript, including its blazing speed, extensive examples, backing by some of the largest software companies globally, and the vast community of active programmers and software engineers.
The program was developed to fulfill the need for performing calculations in a programming language that allows for code reuse in later project stages. JavaScript was chosen for its speed, dynamic nature, interpretability, extensive library support, large existing codebase, backing by major software companies, and the ability to create both desktop and mobile applications.
JavaScript is supported by major industry investments, ensuring continuous innovation and robust development. Our commitment to excellence makes JSLAB a trusted choice for professionals and organizations worldwide.
Join the ranks of top companies who leverage JavaScript for their mission-critical applications. With JSLAB, you benefit from the same reliable and scalable technology that powers some of the most advanced projects on Earth and beyond.
Become part of a vibrant and growing community of JavaScript developers. Extensive support network and active forums ensure you always have the resources and assistance you need to succeed.
JSLAB bridges the gap between JavaScript and specialized scientific tools. Enjoy functionalities equivalent to MATLAB, GNU Octave, Python, R, and Julia, all within a single, unified platform. Perform data analysis, machine learning, numerical computations, and more with ease.
Design intuitive and visually appealing graphical user interfaces using native HTML, CSS, and SVG. Create interactive dashboards, custom visualizations, and responsive layouts without the need for additional frameworks.
Enhance JSLAB’s capabilities by integrating native modules from npm, built with C++ and C. Tap into a vast ecosystem of extensions and customize your environment to meet your specific needs, ensuring maximum performance and flexibility.
Experience the seamless integration of powerful scientific computing and the flexibility of JavaScript. Whether you're developing complex algorithms, analyzing vast datasets, or creating innovative applications, JSLAB empowers you to achieve more.
You can install JSLAB by either downloading the latest stable release from GitHub or by building it from source. Choose the method that best fits your needs.
- Visit the JSLAB Releases Page on GitHub Repository: https://github.com/PR-DC/JSLAB/releases
- Download the appropriate installer and install the program.
- Try examples from: https://github.com/PR-DC/JSLAB/tree/master/examples
Animated 2D plot
A 2D plot animation like this is essential for visualizing real-time data changes, enabling dynamic tracking of evolving values and providing immediate insight into trends or fluctuations as they happen.
var N_buffer = 500;
var t = toc();
var x = createFilledArray(N_buffer, null); x[0] = t;
var y = createFilledArray(N_buffer, null); y[0] = sin(t);
var p = plot({x: x, y: y});
xlabel("x");
ylabel("sin(x)");
title("Simple 2-D Plot");
await p.ready;
setInterval(function() {
var t1 = toc();
x.push(t1);
y.push(sin(t1*2));
if(x.length > N_buffer) {
x.shift();
y.shift();
}
p.update({x: [x], y: [y]}, 0);
}, 33);3D plot with vectors
3D plots are essential for illustrating spatial relationships and complex vector interactions, allowing for a deeper understanding of data across three dimensions.
var x = [0, 0, 0, 1, 0];
var y = [0, 0, 0, 1, 0];
var z = [0, 0, 0, 1, 0];
var u = [1, 0, 0, 1, -1];
var v = [0, 1, 0, 1, 0];
var w = [0, 0, 1, 1, 0];
var head_scale = 0.2;
var head_angleFactor = 0.4;
var vectors = createVectors3D(x, y, z, u, v, w, head_scale, head_angleFactor, {color: "#0f0", width: 6});
figure(1);
plot([
vectors.line, vectors.head
], {'showLegend': false, 'font': {family: 'LatinModern', size: 14}});
xlabel("x");
ylabel("y");
zlabel("z");
xlim([-1, 3]);
ylim([-1, 3]);
zlim([-1, 3]);3D graphics
3D graphics are vital for creating immersive visualizations that bring complex structures and spatial relationships to life, enabling a more intuitive understanding and interaction with digital models in fields like simulation, design, and data analysis.
var win = await openWindow3D();
win.document.title = "Test 3D Window - JSLAB | PR-DC";
var THREE = win.THREE;
const width = win.innerWidth, height = win.innerHeight;
// init
const camera = new THREE.PerspectiveCamera( 70, width / height, 0.01, 10 );
camera.position.z = 1;
const scene = new THREE.Scene();
const geometry = new THREE.BoxGeometry( 0.2, 0.2, 0.2 );
const material = new THREE.MeshNormalMaterial();
const mesh = new THREE.Mesh( geometry, material );
scene.add( mesh );
const renderer = new THREE.WebGLRenderer( { antialias: true } );
renderer.setSize( width, height );
renderer.setAnimationLoop( animate );
win.document.body.appendChild( renderer.domElement );
// Handle window resizing
window.addEventListener('resize', onWindowResize, false);
function onWindowResize() {
camera.aspect = win.innerWidth / win.innerHeight;
camera.updateProjectionMatrix();
renderer.setSize(win.innerWidth, win.innerHeight);
}
function animate( time ) {
mesh.rotation.x = time / 2000;
mesh.rotation.y = time / 1000;
renderer.render( scene, camera );
}Parallel execution
Parallel execution is critical for handling computationally intensive tasks, as it allows multiple operations to run simultaneously, significantly reducing processing time and improving efficiency by utilizing all available CPU cores.
var computeSquare = (i) => i * i;
// Run parallel exectuion
var results = await parallel.parfor(0, 20, 1,
parallel.getProcessorsNum(), {}, undefined, computeSquare);
disp(results);Vector and Matrix operations
Vector and matrix operations are fundamental for efficiently performing complex mathematical computations in fields like physics, engineering, and computer graphics, enabling quick transformations, optimizations, and solutions in multidimensional spaces.
var v1 = vec.new(1, 2, 3);
var v2 = vec.new([4, 8, 6]);
const v_cross = v1.cross(v2);
var A = mat.new([
[1, 2],
[3, 4]
]);
const b = mat.new([
[5],
[11]
]);
const x = A.linsolve(b);
disp('Solution to linear system A * x = b:');
disp(x);Symbolic math
Symbolic math computations are essential for achieving high precision in mathematical modeling, automating algebraic simplifications, and enabling dynamic formula manipulation, which enhances the accuracy and functionality of tools in scientific, engineering, and educational software.
var le, x, E, Iz;
var p, P, invP, N, d2N;
var k_int, k_e_stretching, k_e_torsion;
var xi = range(0, 1, 0.01);
await sym.load();
[le, x, E, Iz] = sym.syms(['le', 'x', 'E', 'Iz']);
P = sym.mat([
[1, 0, 0, 0],
[0, 1, 0, 0],
[1, le, sym.pow(le, 2), sym.pow(le, 3)],
[0, 1, sym.mul(2, le), sym.mul(3, sym.pow(le, 2))]
]);
p = sym.mat([[1, x, sym.pow(x, 2), sym.pow(x, 3)]]);
invP = sym.inv(P);
N = sym.mul(p, invP);
d2N = sym.diff(N, 'x', 2);
k_int = sym.mul(E, Iz, sym.intg(sym.mul(sym.transp(d2N), d2N), x, [0, le]));
Ni = sym.subs(sym.subs(N, le, 1), x, xi).toNumeric();
var N_flat = Ni.flat();
sym.showLatex(N);
sym.showLatex(k_int);FreeCAD Link
Integration with FreeCAD is essential for enabling automated, precise 3D modeling workflows within applications, allowing complex geometries, structures, and engineering designs to be generated, modified, and visualized programmatically, which significantly enhances productivity in design and simulation processes.
var nodes = [
[0, 0, 0],
[0, 10, 0],
[10, 10, 0],
[10, 0, 0],
[0, 0, 10],
[0, 10, 10],
[10, 10, 10],
[10, 0, 10]
];
var D = createFilledArray(nodes.length, 3);
var lines = [];
for(var i = 0; i < 4; i++) {
var j = i+1;
if(i == 3) {
j = 0;
}
lines.push([...nodes[i], ...nodes[j]]);
lines.push([...nodes[i+4], ...nodes[j+4]]);
lines.push([...nodes[i], ...nodes[i+4]]);
}
var d = createFilledArray(lines.length, 1);
// Generate JSON
var nodesFile = pwd + 'out/nodes.json';
var data = {
'Coordinates': nodes,
'Diameters': D
};
writeFile(nodesFile, stringify(data));
var data = {
'Coordinates': lines,
'Diameters': d
};
beamsFile = pwd + 'out/beams.json';
writeFile(beamsFile, stringify(data));
// Run FreeCADLink
await freecad_link.start(exe, {
port: port,
host: host,
timeout: timeout,
startup_timeout: startup_timeout
}); // Start FreeCAD programa
await freecad_link.newDocument(part);
await freecad_link.callScript('MakeNodes', nodesFile, timeout);
await freecad_link.callScript('MakeBeams', beamsFile, timeout);
await freecad_link.callScript('MakeFusion', [], timeout);
await freecad_link.saveAs(model, timeout);
//await freecad_link.quit(); // Close programa
deleteFile(nodesFile);
deleteFile(beamsFile);OpenModelica Link
Integration with OpenModelica is crucial for enabling advanced simulation and analysis of complex dynamic systems directly within applications, allowing engineers to model, test, and optimize system behavior seamlessly, which enhances efficiency in design and validation processes.
await om_link.start(exe); // Start OpenModelica programa
disp(await om_link.sendExpression('getVersion()'));
disp(await om_link.sendExpression("model a end a;"));
disp(await om_link.sendExpression('loadFile("'+model+'")'));
disp(await om_link.sendExpression("getClassNames()"));
disp(await om_link.sendExpression("simulate(BouncingBall)"));
await om_link.close();Comprehensive documentation is available in the root directory of this repository, provided in multiple formats: HTML, PDF, JSON, and TEX for your convenience.
Code references and function details are also accessible directly within JSLAB by using the help() function.
Documentation is also available at: https://pr-dc.com/jslab/doc/
Building from source is intended for advanced users. For details, click here.
In order to download necessary tools, clone the repository, and install dependencies via npm, you need network access.
- Node.js: Ensure that Node.js is installed on your system. You can download it from the official website: https://nodejs.org/
- npm: npm is typically installed alongside Node.js.
- node-gyp: node-gyp is installed alongside the application but it requires additional tools and libraries depending on your operating system. Follow the instructions for your specific OS from: https://github.com/nodejs/node-gyp
- Git: Suggested for cloning the repository. Download it from the official website: https://git-scm.com/
- Clone the JSLAB repository:
git clone https://github.com/PR-DC/JSLAB.git
- Navigate to the project directory:
cd JSLAB - Install the necessary dependencies:
npm install
- Start the application:
npm start
- Check examples from: https://github.com/PR-DC/JSLAB/tree/master/examples
Follow the detailed build instructions available in this documentation.
Follow the coding style and best practices available in this documentation.
- Create a new branch for your feature or bugfix:
git checkout -b feature/your-feature-name
- Make your changes and commit them with clear messages:
git commit -m "Add feature X to improve Y" - Push your branch to your forked repository:
git push origin feature/your-feature-name
- Submit a Pull Request (PR) detailing your changes.
Before submitting a PR, ensure that all tests pass and add new tests for any new functionality you introduce.
All PRs are subject to review by the maintainers. Be prepared to make revisions based on feedback to align with project standards.
- Consistent Formatting: Use a consistent code formatter (e.g., Prettier) to maintain uniform code style.
- Meaningful Commit Messages: Write clear and descriptive commit messages that explain the purpose of the changes.
- Modular Code: Write reusable and modular code to enhance maintainability and scalability.
- Comprehensive Testing: Implement thorough tests to ensure the reliability of your contributions.
Your feedback is invaluable in improving the JSLAB Library. Whether you encounter bugs, have feature requests, or need assistance, please reach out through the following channels:
- GitHub Issues: Report bugs or suggest features by opening an issue in the GitHub repository.
- Email: Contact us directly at [email protected] or main author at [email protected].
We encourage active participation and appreciate all forms of feedback that help us enhance the functionality and usability of JSLAB.
Copyright (C) 2024 PR-DC <[email protected]>
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU Lesser General Public License as
published by the Free Software Foundation, either version 3 of the
License, or (at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU Lesser General Public License for more details.
You should have received a copy of the GNU Lesser General Public License
along with this program. If not, see <https://www.gnu.org/licenses/>.