Merge pull request #134 from arrudacaio/master

adiciona resumo de IC

ic/resumos/sistemasDeNumeracao.md

@@ -0,0 +1,84 @@
+# Sistemas de Numeração
+Conjunto de símbolos utilizados para representação de quantidades e de regras que definem a forma de apresentação. Cada sistema de numeração é apenas um método diferente para representar quantidades. 
+
+_**As quantidades em si não mudam, apenas a forma de representá-las**_
+
+| **Sistema** | **Base** | **Algarismos** | 
+| :---: | :---: | :---: |
+| Binário | 2 | 0, 1 |
+| Octal | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
+| Decimal | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
+| Hexadecimal | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
+
+### Tabela Comparativa
+
+| **Decimal** | **Binário** | **Octal** | **Hexadecimal** |
+| :---: | :---: | :---: | :---: |
+| 0  | 0000 | 0  |  0 |
+| 1  | 0001 | 1  |  1 |
+| 2  | 0010 | 2  |  2 |
+| 3  | 0011 | 3  |  3 |
+| 4  | 0100 | 4  |  4 |
+| 5  | 0101 | 5  |  5 |
+| 6  | 0110 | 6  |  6 |
+| 7  | 0111 | 7  |  7 |
+| 8  | 1000 | 10 |  8 |
+| 9  | 1001 | 11 |  9 |
+| 10 | 1010 | 12 |  A |
+| 11 | 1011 | 13 |  B |
+| 12 | 1100 | 14 |  C |
+| 13 | 1101 | 15 |  D |
+| 14 | 1110 | 16 |  E |
+| 15 | 1111 | 17 |  F |
+
+
+## Conversão entre Sistemas de Numeração
+
+### Decimal para qualquer Base Númerica:
+
+Para realizar a conversão de decimal para binário, realiza-se a _**divisão sucessiva pela base de destino**_ (por exemplo, se for para hexadecimal, deve-se dividir por 16). O resultado da conversão será dado pelo último quociente (MSB) e o agrupamento dos restos de divisão será o número na base de destino.
+
+Por exemplo, vamos converter o número 45 em binário:
+
+![Imagem 1](https://www.embarcados.com.br/wp-content/uploads/2016/07/decimal-bin%C3%A1rio.jpg)
+
+A leitura do resultado é feita do último quociente para o primeiro resto. Sendo assim, o resultado da conversão do número 45 para binário é: **101101**(2).
+
+Agora, vamos converter o número 10024 para hexadecimal:
+
+![Imagem 2](http://www.mecaweb.com.br/eletronica/content/image/conv_dh_2.png)
+
+## Qualquer Base Numérica para Decimal:
+
+Nesse caso, deve-se utilizar notação polinomial.
+
+![Imagem 3](https://image.slidesharecdn.com/03stcunidadesdeinformacaosistemasnumericos-150303110419-conversion-gate01/95/unidades-de-informacao-sistemas-numericos-39-638.jpg?cb=1425402323)
+
+Por exemplo, vamos converter o número A3 (em hexadecimal) para decimal:
+
+![Imagem 4](https://rvalentim.files.wordpress.com/2010/01/hexadec-decimal.jpg)
+
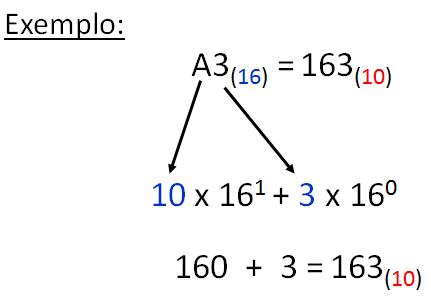+## Octal/Hexadecimal para Binário (e vice-versa): 
+
+Deve-se utilizar a técnica de **agrupamento de bits**, associando 3 ou 4 bits a cada algarismo de octal ou hexadecimal, respectivamente.
+
+Como exemplo, vamos converter 21, em octal e em hexadecimal, para binário: 
+
+![Imagem 5](http://mundoprojetado.com.br/wp-content/uploads/2019/01/Conversao-de-octal-hexa-para-binario.png)
+
+A seguir, vamos converter 001000110 de binário para octal e hexadecimal:
+
+![Imagem 6](http://mundoprojetado.com.br/wp-content/uploads/2019/01/Conversao-de-bin%C3%A1rio-em-octal-hexa.png)
+
+## Octal para Hexadecimal (e vice-versa):
+
+Nesse caso, a conversão não é realizada diretamente e requer o uso de uma **base intermediária (base binária)**. Para esse tipo de conversão, é necessário seguir dois passos:
+
+1. Converter o número da base original (octal ou hexadecimal) para binário.
+2. Converter o resultado binário para a base destino (hexadecimal ou octal).
+
+Por exemplo, vamos converter 175 em octal para hexadecimal:
+
+(**175**) 8 = (**?**) 16
+
+(**175**) *8* = (**1111101**) *2* =  (**7D**) *16*