OpenDR also performs approximate differentiation of rasterization. However, its behavior is very different from our Neural Renderer. Here, we compare them from two perspectives.
The derivative of OpenDR considers only the pixels on the edge, but our derivatives account for distant pixels.
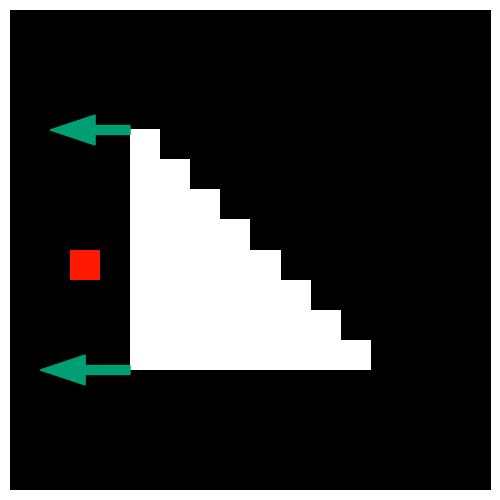
The figures below are examples of differentiation of OpenDR. The loss function is "the pixel painted blue should be darker." The green arrow represents the direction in which the vertex moves by the gradient descent, using the calculated derivative. When the blue pixel is outside the polygon, or when it is more than two pixels away from the edge, we can see that the gradients propagated to the vertices are zero.
The figures below are examples of differentiation of Neural Renderer. Even if the blue pixel is more than two pixels away from the edge, the gradient does not become zero. Also, due to this effect, the vertices have non-zero vertical gradients.
In practical applications, important supervision signals do not necessarily appear on the edges of polygons. Therefore, our gradients are more suitable for the optimization of vertices.
In the above examples, the loss function was "the specified pixel should be darker". Rather, what happens when the loss function is "the specified pixel should be brighter"?
The figure below shows the gradients in OpenDR using this loss function. In the third image, the vertices are about to move to the left. However, even if they move, the specified pixel should not be brighter.
Neural Renderer propagates gradients so that the value of the objective function becomes small. The figures below show this.
If the objective function is "the specified pixel should be brighter," the gradient by OpenDR cannot be used for optimization, while Neural Renderer calculates the desired gradient. This is accomplished by using the gradient back-propagated from the objective function to the renderer. This is the intention that we say "the backward pass of our renderer is designed for neural networks."