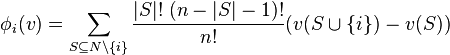the-shapley-value

Source code of the algorithm (in lua) to calculate the Shapley Value, one of the main concepts from Cooperative Game Theory.

Understand how it works: https://en.wikipedia.org/wiki/Shapley_value

The algorithm is defined by the given formula:

Take care with the sum set notation. All the S subsets from N \ {i} generated from permutation respects this rule, but you don't use all the subsets to calculate the shapley value. You need to remove the duplicated elements:

Correct interpretation of set to be iterated in sum:

function shapleyValueActionSet(N, i)
	local P = powerSet(N)
	local R = set{}

	forEach(P, function(p)
		local subset = set{subtract(p, set{i})}
		if not isSubsetOrEquals(subset, R) then R = union(R, subset) end
	end)

	return R
end

Wrong interpretation of set to be iterated in sum:

function shapleyValueActionSet(N, i)
	local P = powerSet(N)
	local R = set{}

	forEach(P, function(p)
		local subset = set{subtract(p, set{i})}
		R = union(R, subset) --Here is the problem, you'll have duplicated elements
	end)

	return R
end

I also tried to play with permutations:

-- Returns the set which will be iterated in sum in shapley value algorithm, using set generated from permutations of N elements
-- It's slower than shapleyValueActionSet
function shapleyValueActionSetPermutations(N, i)
	local permutations = permutations(setToArray(N))
	local R = set{}

	forEach(permutations, function(_, p)
		local newSet = set{}

		forEach(p, function(_, v)
			if v == i then
				local subset = set{newSet}
				if not isSubsetOrEquals(subset, R) then R = union(R, subset) end
				--R = union(R, subset)
				return "BREAK"
			end
			newSet[v] = true
		end)
	end)

	return R
end

-- Return all the possible permutations from array (|array|!)
function permutations(array)
	if #array == 1 then
		return array
	elseif #array == 2 then
		return {{array[1], array[2]}, {array[2], array[1]}}
	else
		local result = {}
		__recursivePermutations(array, result, 1)
		return result
	end
end

The code try to follow the formula literally as a study case, instead of be the most optimized. Just let me know if you have some doubts or suggestions. I really would appreciate if you test it in more Coalitional Game cases.

Made with Lua 5.3.2