Discussion 8: Linked Lists, Efficiency
NEW: From now on, we'll still use Pensieve, but we've removed the voice chat from Pensieve. Use Discord for voice chat with the course staff. It's more reliable and includes screensharing. Write to @discuss in the #discuss-queue channel on Discord at any time, and a member of the course staff will join your voice channel.
Pick someone in your group to join Discord. It's fine if multiple people join, but one is enough.
Now switch to Pensieve:
- Everyone: Go to discuss.pensieve.co and log in with your @berkeley.edu email, then enter your group number. (Your group number is the number of your Discord channel.)
Once you're on Pensieve, you don't need to return to this page; Pensieve has all the same content (but more features). If for some reason Penseive doesn't work, return to this page and continue with the discussion.
Post in the #help channel on Discord if you have trouble.
Getting Started
If you have only 1 or 2 people in your group, you can join the other group in the room with you.
Everybody say your name and your birthday and then tell the group about your favorite birthday party you've attended (either for your birthday or someone else's).
Pro tip: Groups tend not to ask for help unless they've been stuck for a looooooong time. Try asking for help sooner. We're pretty helpful! You might learn something.
Linked Lists
A linked list is a Link object or Link.empty.
You can mutate a Link object s in two ways:
- Change the first element with
s.first = ... - Change the rest of the elements with
s.rest = ...
You can make a new Link object by calling Link:
-
Link(4)makes a linked list of length 1 containing 4. -
Link(4, s)makes a linked list that starts with 4 followed by the elements of linked lists.class Link: """A linked list is either a Link object or Link.empty >>> s = Link(3, Link(4, Link(5))) >>> s.rest Link(4, Link(5)) >>> s.rest.rest.rest is Link.empty True >>> s.rest.first * 2 8 >>> print(s) <3 4 5> """ empty = () def init(self, first, rest=empty): assert rest is Link.empty or isinstance(rest, Link) self.first = first self.rest = rest def repr(self): if self.rest: rest_repr = ', ' + repr(self.rest) else: rest_repr = '' return 'Link(' + repr(self.first) + rest_repr + ')' def str(self): string = '<' while self.rest is not Link.empty: string += str(self.first) + ' ' self = self.rest return string + str(self.first) + '>'
Facilitator: Pick a way for your group to draw diagrams. Paper, a whiteboard, or a tablet, are all fine. If you don't have anything like that, ask the other group in the room if they have extra paper.
Q1: Strange Loop
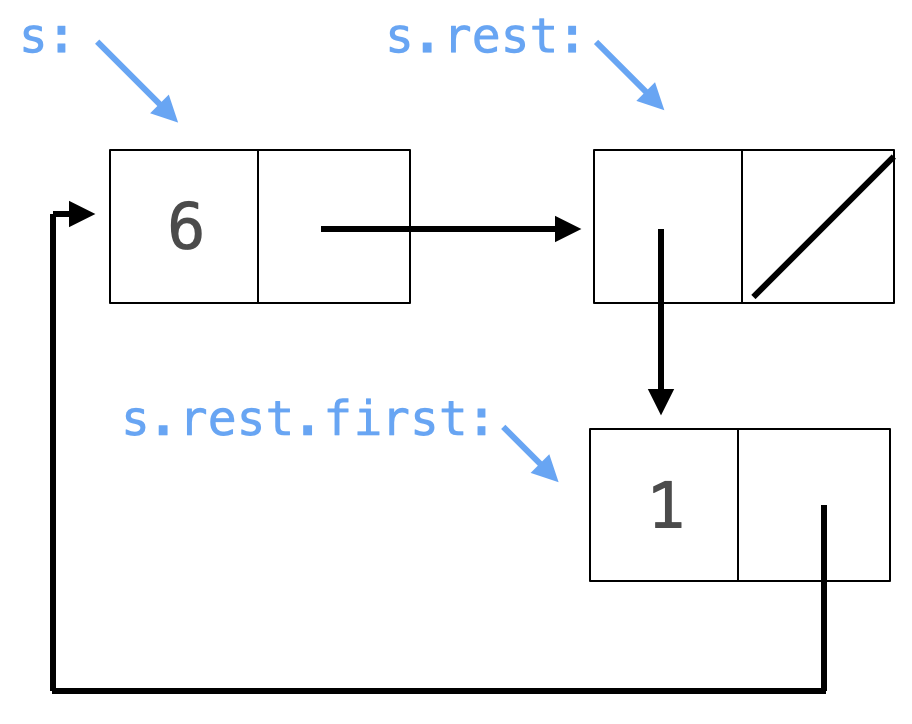
In lab, there was a Link object with a cycle that represented an infinite repeating list of 1's.
>>> ones = Link(1)>>> ones.rest = ones>>> [ones.first, ones.rest.first, ones.rest.rest.first, ones.rest.rest.rest.first][1, 1, 1, 1]>>> ones.rest is onesTrue
Implement strange_loop, which takes no arguments and returns a Link object s for which s.rest.first.rest is s.
Draw a picture of the linked list you want to create, then write code to create it.
Facilitator: When you think everyone has had a chance to read this far, please say: "So, what is this thing going to look like?"
For s.rest.first.rest to exist at all, the second element of s, called s.rest.first, must itself be a linked list.
Making a cycle requires two steps: making a linked list without a cycle, then modifying it. First create, for example, s = Link(6, Link(Link(1))), then change s.rest.first.rest to create the cycle.
Run in 61A Code
Q2: Sum Two Ways
Implement both sum_rec and sum_iter. Each one takes a linked list of numbers s and returns the sum of its elements. Use recursion to implement sum_rec. Don't use recursion to implement sum_iter; use a while loop instead.
Facilitator: Tell the group which one to start with. It's your choice. You can say: "Let's start with the recursive version."
Run in 61A Code
Add s.first to the sum of the elements in s.rest. Your base case condition should be s is Link.empty so that you're checking whether s is empty before ever evaluating s.first or s.rest.
Introduce a new name, such as total, then repeatedly (in a while loop) add s.first to total and set s = s.rest to advance through the linked list, as long as s is not Link.empty.
Discussion time: When adding up numbers, the intermediate sums depend on the order.
(1 + 3) + 5 and 1 + (3 + 5) both equal 9, but the first one makes 4 along the way while the second makes 8 along the way. For the same linked list, will sum_rec and sum_iter both make the same intermediate sums along the way? Answer in your group's Discord channel's text chat. If yes, post "Same way all day." If no, post "Sum thing is different."
Q3: Overlap
Implement overlap, which takes two linked lists of numbers called s and t that are sorted in increasing order and have no repeated elements within each list. It returns the count of how many numbers appear in both lists.
This can be done in linear time in the combined length of s and t by always advancing forward in the linked list whose first element is smallest until both first elements are equal (add one to the count and advance both) or one list is empty (time to return). Here's a lecture video clip about this (but the video uses Python lists instead of linked lists).
Take a vote to decide whether to use recursion or iteration. Either way works (and the solutions are about the same complexity/difficulty).
Want some guidance? Post @discuss over here! and your group number to the #discuss-queue channel on Discord.
Run in 61A Code
if s is Link.empty or t is Link.empty: return 0 if s.first == t.first: return __________________ elif s.first < t.first: return __________________ elif s.first > t.first: return __________________
k = 0 while s is not Link.empty and t is not Link.empty: if s.first == t.first: __________________ elif s.first < t.first: __________________ elif s.first > t.first: __________________ return k
Q4: Overlap Growth
The alternative implementation of overlap below does not assume that s and t are sorted in increasing order. What is the order of growth of its run time in terms of the length of s and t, assuming they have the same length? Choose among: constant, logarithmic, linear, quadratic, or exponential.
def length(s): if s is Link.empty: return 0 else: return 1 + length(s.rest)def filter_link(f, s): if s is Link.empty: return s else: frest = filter_link(f, s.rest) if f(s.first): return Link(s.first, frest) else: return frestdef contained_in(s): def f(s, x): if s is Link.empty: return False else: return s.first == x or f(s.rest, x) return lambda x: f(s, x)def overlap(s, t): """For s and t with no repeats, count the numbers that appear in both. >>> a = Link(3, Link(4, Link(6, Link(7, Link(9, Link(10)))))) >>> b = Link(1, Link(3, Link(5, Link(7, Link(8, Link(12)))))) >>> overlap(a, b) # 3 and 7 2 >>> overlap(a.rest, b.rest) # just 7 1 >>> overlap(Link(0, a), Link(0, b)) 3 """ return length(filter_link(contained_in(t), s))
Document the Occasion
Please all fill out the attendance form (one submission per person per week).
Important: Please help put the furniture in the room back where you found it before you leave. Thanks!
This last question is similar in complexity to an A+ question on an exam. Feel free to skip it, but it's a fun one, so try it if you have time.
Q5: Decimal Expansion
Definition. The decimal expansion of a fraction n/d with n < d is an infinite sequence of digits starting with the 0 before the decimal point and followed by digits that represent the tenths, hundredths, and thousands place (and so on) of the number n/d. E.g., the decimal expansion of 2/3 is a zero followed by an infinite sequence of 6's: 0.6666666....
Implement divide, which takes positive integers n and d with n < d. It returns a linked list with a cycle containing the digits of the infinite decimal expansion of n/d. The provided display function prints the first k digits after the decimal point.
For example, 1/22 would be represented as x below:
>>> 1/220.045454545454545456>>> x = Link(0, Link(0, Link(4, Link(5))))>>> x.rest.rest.rest.rest = x.rest.rest>>> display(x, 20)0.04545454545454545454...
Run in 61A Code
The decimal expansion of 1/22 could be constructed as follows:
>>> n, d = 1, 22>>> n/d0.045454545454545456>>> result = Link(0)>>> tail = result>>> q, r = 10 * n // d, 10 * n % d>>> tail.rest = Link(q) # Adds the 0: 0.0>>> tail = tail.rest>>> n = r>>> n10>>> q, r = 10 * n // d, 10 * n % d>>> tail.rest = Link(q) # Adds the 4: 0.04>>> tail = tail.rest>>> n = r>>> n12>>> q, r = 10 * n // d, 10 * n % d>>> tail.rest = Link(q) # Adds the 5: 0.045>>> tail = tail.rest>>> n = r>>> n10>>> resultLink(0, Link(0, Link(4, Link(5))))>>> tail.rest = result.rest.rest>>> display(result, 20)0.04545454545454545454...
Place the division pattern from the example above in a while statement:
>>> q, r = 10 * n // d, 10 * n % d>>> tail.rest = Link(q)>>> tail = tail.rest>>> n = r
While constructing the decimal expansion, store the tail for each n in a dictionary keyed by n. When some n appears a second time, instead of constructing a new Link, set its original link as the rest of the previous link. That will form a cycle of the appropriate length.