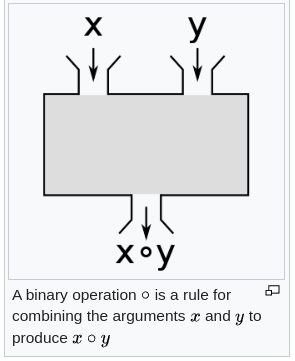
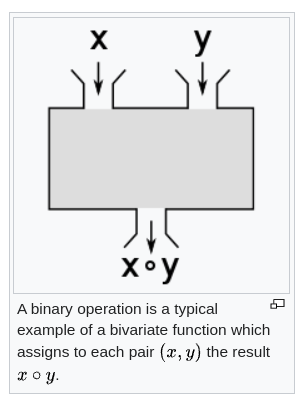
What is Functional Programming ? It's a programming paradigm that uses Expressions as the building blocks of the code.
In contrast, Imperative Programming is a paradigm that uses Statements to control the flow of the code.
fp60-101i.mp4
Both programming paradigms have expressions and statements, but in Functional Programming, expressions are primarily used to compose other expressions, while in Imperative Programming, statements are primarily used to control the flow of execution.
💡 How does Functional Programming Code Drive?
In mathematics and programming, an expression is a combination of values, operators and functions .
fp60-202e.mp4
These elements follow a set of associativity and precedence rules to determine the order of evaluation .
The expression ultimately produces a single resolved value. In programming, this resolved value can also be considered an expression itself.
Expressions are essential tools for representing calculations and manipulating data in both mathematics and programming.
Their ability to combine values, operators and functions with defined evaluation rules makes them possible building blocks for Functional Programming.
fp60-203a.mp4
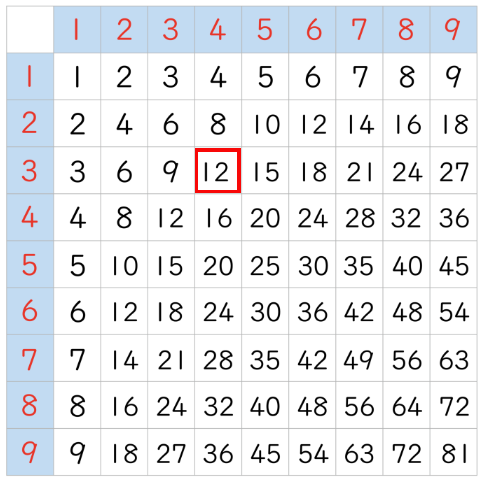
In mathematics, a binary operation is a rule that combines two elements , called operands , to produce another element using an operator.
The most common binary operations are addition , subtraction , multiplication , and division , collectively known as the four basic arithmetic operations .
Here
These combine two numbers to produce a new number.
These operations are widely used in everyday life, throughout mathematics, and in various programming languages.
Therefore, fundamentally, operators are functions.
https://dev.epicgames.com/documentation/en-us/uefn/operators-in-verse
Operators are special functions defined in the Verse programming language to perform actions such as the math operations for addition and multiplication.
In F#, infix binary operators can also be written as prefix functions.
1 + 2 // 3
(+) 1 2 // 3In essence, symbols like
1 + 2 // F#/Haskell/JavaScript
(+) 1 2 // F#/Haskell
plus 1 2 // F#/Haskell
plus(1)(2) // F#/Haskell/JavaScriptMath.pow(2, 3) // 8
2 ** 3 // 8In Functional Programming languages, functions are expressions.
In other words, functions are treated as first-class values . This means they can be assigned to variables, passed as arguments, and returned from other functions.
First-class function is the fundamental requirement for a programming language to be considered a Functional Programming language.
In C, functions are not first-class values, which means they cannot be treated as expressions. This lack of first-class functions prevents C from being considered a Functional Programming language.
Functions in JavaScript/TypeScript and F# are first-class values, which are expressions. Therefore, both JavaScript/TypeScript and F# can be classified as Functional Programming languages.
First-class functions naturally lead us to the concept of higher-order functions, which become incredibly powerful tools in Functional Programming.
Let's investigate a case in which a function returns first-class function.
This can be written as:
3 * 4 // F#/Haskell/JavaScript
(*) 3 4 // F#/Haskell
times 3 4 // F#/Haskell
times(3)(4) // F#/Haskell/JavaScriptlet times =
a =>
b => a * b
let times3 =
times(3)times(3) returns another function: times3.
times3 is a function as the table:
let times34 =
times3(4) // 12
times(3)(4) // 12In F#, we don't need to use parentheses, so this is simply written as times 3 4.
let times =
fun a ->
fun b ->
a * b
let times34 =
times 3 4 // 12A function like this is called a Higher-order_function.
Converting a binary function like times(3, 4) into a higher-order function is often called currying.
times(3, 4)↓
times(3)(4)times 3 4 In mathematics and computer science, a higher-order function (HOF) is a function that does at least one of the following:
- takes one or more functions as arguments (i.e. a procedural parameter, which is a parameter of a procedure that is itself a procedure),
- returns a function as its result.
As a result, we will have only 3 cases as below:
function: value -> function
function: function -> value
function: function -> function
In this case, times(3) returns another function: times3.
So, this is a higher-order function which returns a function as it's result.
function: value -> function
Let's investigate a case in which a function (operator) takes first-class function.
function: function -> value
There is a less familier binary operation called Pipeline (operation).
The pipe operator |> takes function as the operand, which allows you to establish "pipelines" of functions in a flexible manner.
|>
a |> function
This operator extremely important and is used extensively when processing data in F#.
The Pipe operator is a function , which is simply defined as:
let (|>) x f = f xMathematics and Functional Programming: Omitting Parentheses
In mathematics, it is common practice to omit parentheses when applying functions, especially in advanced mathematical texts and papers. This is particularly evident with trigonometric functions like sine , where
is often written simply as:
Similarly, in programming languages like F# and Haskell, function application f(x) is often written as f x (with a space between the function name and argument) when the context is clear. This style omits parentheses, which are considered redundant in these languages.
let f = fun x -> x + 1
let x = 1
let y = f x // 2
let z = x |> f // 2Let's consider a function named double that takes a value and returns its double.
let double x =
x * 2let result1 =
double(1)
let result1' =
1 |> double
// 2let result2 =
double(double(1))
let result2' =
1 |> double |> double
// 4The pipe operator |> eliminates the complicated nesting of ( ) notation and creates a clean pipeline by sequentially applying double functions to the data 1.
let f = fun x -> x + 1
let g = fun x -> x * 2
let x = 1
let y = g (f x) // 4
let z = x |> f |> g // 4let output =
input
|> function1
|> function2
|> function3double is a function that takes a value and returns a value .
List.reduce is a function that takes a function and returns a function .
function: function -> function
See Advanced operator for iteration in 💡 How does Functional Programming Code Drive?
let reducer =
List.reduce (+)List.reduce (+) takes a function: (+) and returns a function: reducer .
let sum =
[0;1;2;3;4;5]
|> reducer // pipeline operation
//15It's also possible to rewrite:
let sum =
[0;1;2;3;4;5]
|> List.reduce (+)
// 15list |> reduce function
It can be interpreted as creating a new binary operator:
list |> map function
This is also a less familier binary operation called Endo-functor.
list |> bind monadicFunction
This is also a less familier binary operation called Monad.
- Function
- Monadic function (Kleisli arrow)
- (Endo)Functor and Monad are two sides of the same mathematical structure
- (Endo)Functor / Monad with
$id$ /$ID$
- Functions with Pipeline - Function composition
-
(Endo)Functor- Functions are linked/composed with Pipeline, including both the contents and the shell of the container
-
Monad - link/composition of Monadic functions =Kleisli composition
- (Endo)Functor- Functions are linked/composed with Pipeline, including both the contents and the shell of the container
- Monad - link/composition of Monadic functions =Kleisli composition