05.Array-Merge-Sort.md

1. 归并排序算法思想

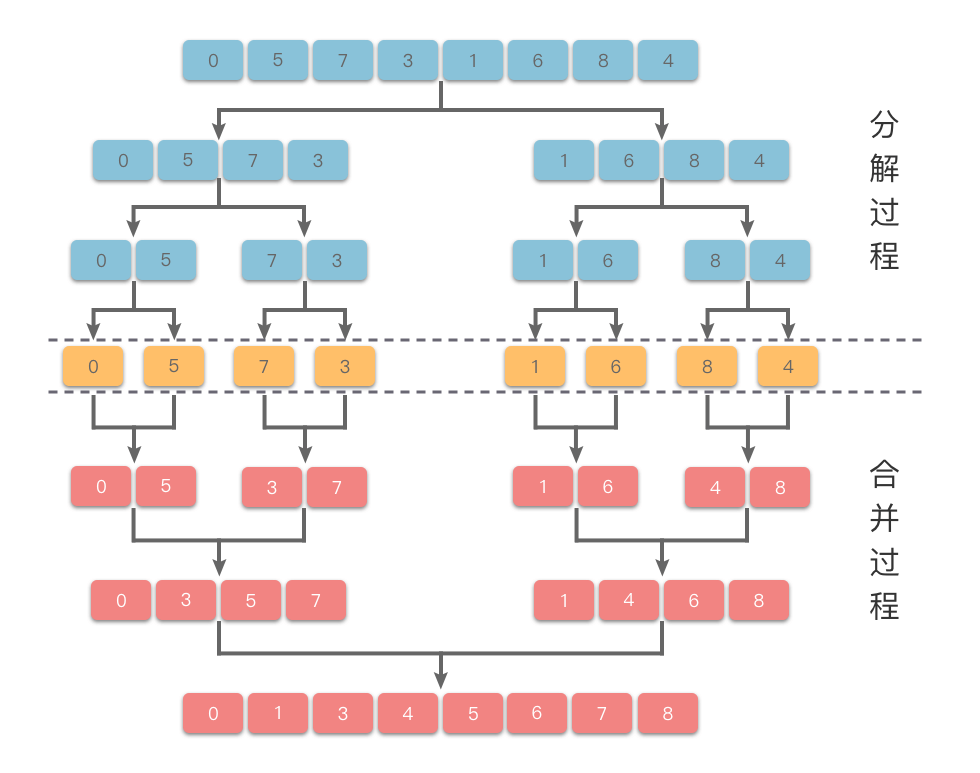
归并排序（Merge Sort）基本思想：

采用经典的分治策略，先递归地将当前数组平均分成两半，然后将有序数组两两合并，最终合并成一个有序数组。

2. 归并排序算法步骤

假设数组的元素个数为 $n$ 个，则归并排序的算法步骤如下：

1. 分解过程：先递归地将当前数组平均分成两半，直到子数组长度为 $1$。
   1. 找到数组中心位置 $mid$，从中心位置将数组分成左右两个子数组 $left\underline{\hspace{0.5em}}nums$、$right\underline{\hspace{0.5em}}nums$。
   2. 对左右两个子数组 $left\underline{\hspace{0.5em}}nums$、$right\underline{\hspace{0.5em}}nums$ 分别进行递归分解。
   3. 最终将数组分解为 $n$ 个长度均为 $1$ 的有序子数组。
2. 归并过程：从长度为 $1$ 的有序子数组开始，依次将有序数组两两合并，直到合并成一个长度为 $n$ 的有序数组。
   1. 使用数组变量 $nums$ 存放合并后的有序数组。
   2. 使用两个指针 $left\underline{\hspace{0.5em}}i$、$right\underline{\hspace{0.5em}}i$ 分别指向两个有序子数组 $left\underline{\hspace{0.5em}}nums$、$right\underline{\hspace{0.5em}}nums$ 的开始位置。
   3. 比较两个指针指向的元素，将两个有序子数组中较小元素依次存入到结果数组 $nums$ 中，并将指针移动到下一位置。
   4. 重复步骤 $3$，直到某一指针到达子数组末尾。
   5. 将另一个子数组中的剩余元素存入到结果数组 $nums$ 中。
   6. 返回合并后的有序数组 $nums$。

我们以 $[0, 5, 7, 3, 1, 6, 8, 4]$ 为例，演示一下归并排序算法的整个步骤。

3. 归并排序代码实现

class Solution:
    # 合并过程
    def merge(self, left_nums: [int], right_nums: [int]):
        nums = []
        left_i, right_i = 0, 0
        while left_i < len(left_nums) and right_i < len(right_nums):
            # 将两个有序子数组中较小元素依次插入到结果数组中
            if left_nums[left_i] < right_nums[right_i]:
                nums.append(left_nums[left_i])
                left_i += 1
            else:
                nums.append(right_nums[right_i])
                right_i += 1
        
        # 如果左子数组有剩余元素，则将其插入到结果数组中
        while left_i < len(left_nums):
            nums.append(left_nums[left_i])
            left_i += 1
        
        # 如果右子数组有剩余元素，则将其插入到结果数组中
        while right_i < len(right_nums):
            nums.append(right_nums[right_i])
            right_i += 1
        
        # 返回合并后的结果数组
        return nums

    # 分解过程
    def mergeSort(self, nums: [int]) -> [int]:
        # 数组元素个数小于等于 1 时，直接返回原数组
        if len(nums) <= 1:
            return nums
        
        mid = len(nums) // 2                        # 将数组从中间位置分为左右两个数组
        left_nums = self.mergeSort(nums[0: mid])    # 递归将左子数组进行分解和排序
        right_nums =  self.mergeSort(nums[mid:])    # 递归将右子数组进行分解和排序
        return self.merge(left_nums, right_nums)    # 把当前数组组中有序子数组逐层向上，进行两两合并

    def sortArray(self, nums: [int]) -> [int]:
        return self.mergeSort(nums)

4. 归并排序算法分析

• 时间复杂度：$O(n \times \log n)$。归并排序算法的时间复杂度等于归并趟数与每一趟归并的时间复杂度乘积。子算法 merge(left_nums, right_nums): 的时间复杂度是 $O(n)$，因此，归并排序算法总的时间复杂度为 $O(n \times \log n)$。
• 空间复杂度：$O(n)$。归并排序方法需要用到与参加排序的数组同样大小的辅助空间。因此，算法的空间复杂度为 $O(n)$。
• 排序稳定性：因为在两个有序子数组的归并过程中，如果两个有序数组中出现相等元素，merge(left_nums, right_nums): 算法能够使前一个数组中那个相等元素先被复制，从而确保这两个元素的相对顺序不发生改变。因此，归并排序算法是一种 稳定排序算法。