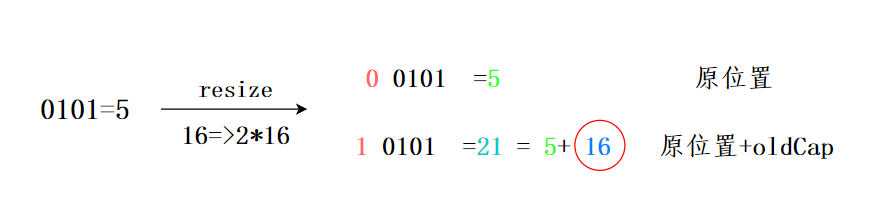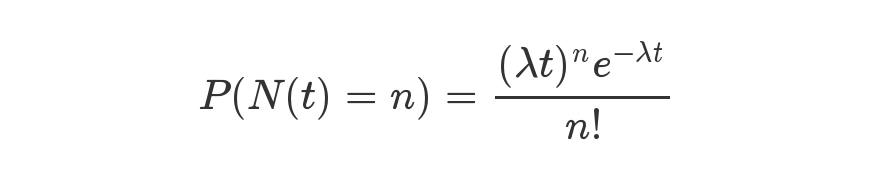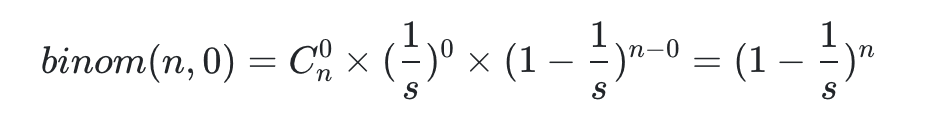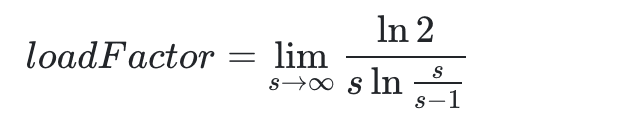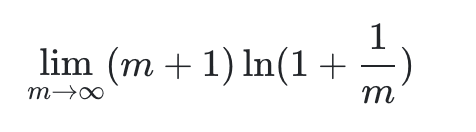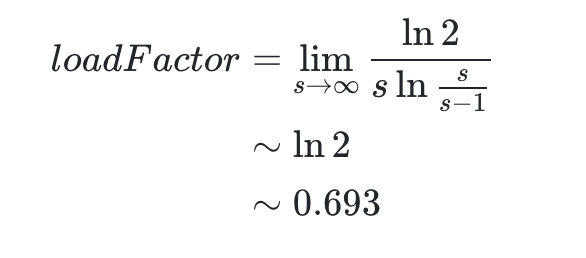title

shortTitle

01、hash 方法的原理

简单了解 HashMap 后，我们来讨论第一个问题：hash 方法的原理，对吃透 HashMap 会大有帮助。

来看一下 hash 方法的源码（JDK 8 中的 HashMap）：

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

这段代码究竟是用来干嘛的呢？

将 key 的 hashCode 值进行处理，得到最终的哈希值。

怎么理解这句话呢？不要着急。

我们来 new 一个 HashMap，并通过 put 方法添加一个元素。

HashMap<String, String> map = new HashMap<>();
map.put("chenmo", "沉默");

来看一下 put 方法的源码。

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

看到 hash 方法的身影了吧？

hash 方法的作用

前面也说了，HashMap 的底层是通过数组的形式实现的，初始大小是 16（这个后面会讲），先记住。

也就是说，HashMap 在添加第一个元素的时候，需要通过键的哈希码在大小为 16 的数组中确定一个位置（索引），怎么确定呢？

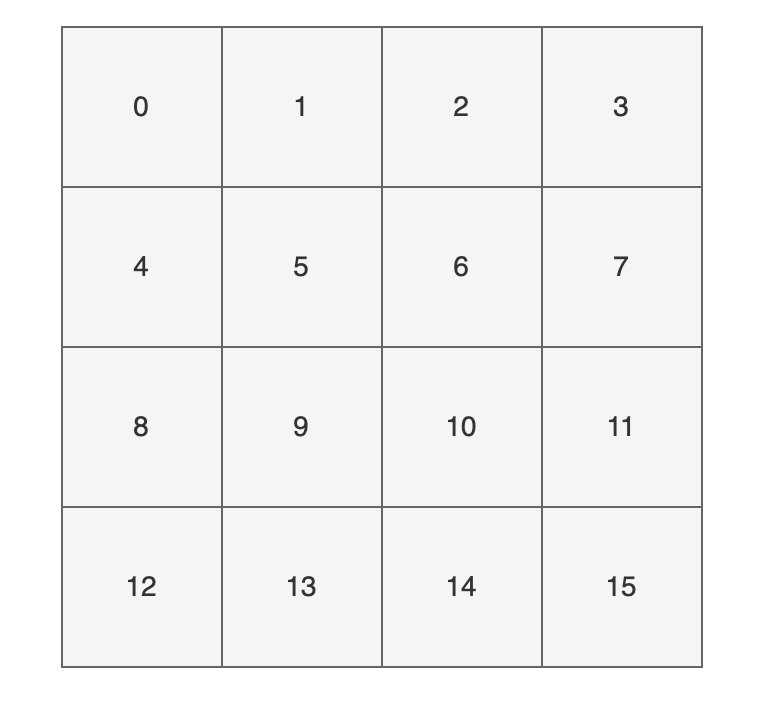
为了方便大家直观的感受，我这里画了一副图，16 个方格子（可以把它想象成一个一个桶），每个格子都有一个编号，对应大小为 16 的数组下标（索引）。

现在，我们要把 key 为 “chenmo”，value 为“沉默”的键值对放到这 16 个格子中的一个。

怎么确定位置（索引）呢？

我先告诉大家结论，通过这个与运算 (n - 1) & hash，其中变量 n 为数组的长度，变量 hash 就是通过 hash() 方法计算后的结果。

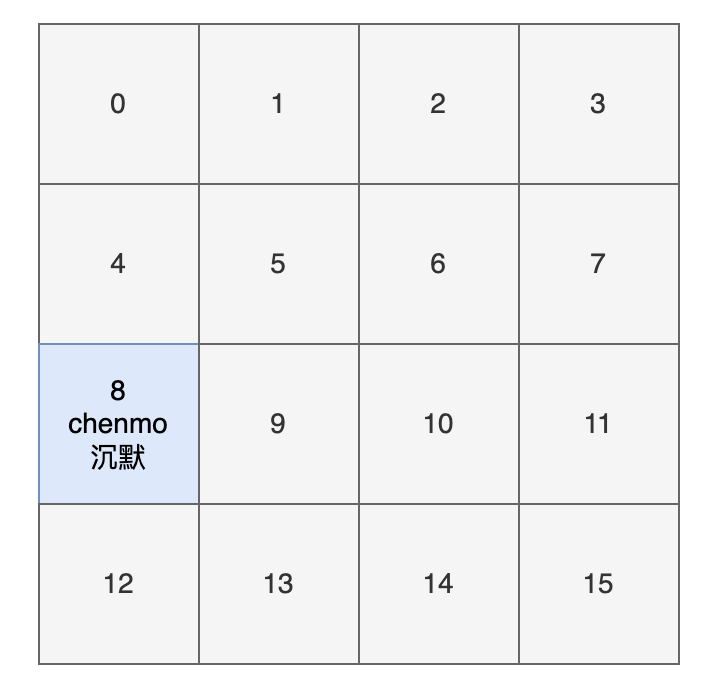
那“chenmo”这个 key 计算后的位置（索引）是多少呢？

答案是 8，也就是说 map.put("chenmo", "沉默") 会把 key 为 “chenmo”，value 为“沉默”的键值对放到下标为 8 的位置上（也就是索引为 8 的桶上）。

这样大家就会对 HashMap 存放键值对（元素）的时候有一个大致的印象。其中的一点是，hash 方法对计算键值对的位置起到了至关重要的作用。

回到 hash 方法：

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

下面是对该方法的一些解释：

参数 key：需要计算哈希码的键值。
key == null ? 0 : (h = key.hashCode()) ^ (h >>> 16)：这是一个三目运算符，如果键值为 null，则哈希码为 0（依旧是说如果键为 null，则存放在第一个位置）；否则，通过调用hashCode()方法获取键的哈希码，并将其与右移 16 位的哈希码进行异或运算。
^ 运算符：异或运算符是 Java 中的一种位运算符，它用于将两个数的二进制位进行比较，如果相同则为 0，不同则为 1。
h >>> 16：将哈希码向右移动 16 位，相当于将原来的哈希码分成了两个 16 位的部分。
最终返回的是经过异或运算后得到的哈希码值。

这短短的一行代码，汇聚不少计算机巨佬们的聪明才智。

理论上，哈希值（哈希码）是一个 int 类型，范围从-2147483648 到 2147483648。

前后加起来大概 40 亿的映射空间，只要哈希值映射得比较均匀松散，一般是不会出现哈希碰撞（哈希冲突会降低 HashMap 的效率）。

但问题是一个 40 亿长度的数组，内存是放不下的。HashMap 扩容之前的数组初始大小只有 16，所以这个哈希值是不能直接拿来用的，用之前要和数组的长度做与运算（前文提到的 (n - 1) & hash，有些地方叫取模预算，有些地方叫取余运算），用得到的值来访问数组下标才行。

取模运算 VS 取余运算 VS 与运算

那这里就顺带补充一些取模预算/取余运算和与运算的知识点哈。

取模运算（Modulo Operation）和取余运算（Remainder Operation）从严格意义上来讲，是两种不同的运算方式，它们在计算机中的实现也不同。

在 Java 中，通常使用 % 运算符来表示取余，用 Math.floorMod() 来表示取模。

当操作数都是正数的话，取模运算和取余运算的结果是一样的。
只有当操作数出现负数的情况，结果才会有所不同。
取模运算的商向负无穷靠近；取余运算的商向 0 靠近。这是导致它们两个在处理有负数情况下，结果不同的根本原因。
当数组的长度是 2 的 n 次方，或者 n 次幂，或者 n 的整数倍时，取模运算/取余运算可以用位运算来代替，效率更高，毕竟计算机本身只认二进制嘛。

我们通过一个实际的例子来看一下。

int a = -7;
int b = 3;

// a 对 b 取余
int remainder = a % b;
// a 对 b 取模
int modulus = Math.floorMod(a, b);

System.out.println("数字: a = " + a + ", b = " + b);
System.out.println("取余 (%): " + remainder);
System.out.println("取模 (Math.floorMod): " + modulus);

// 改变 a 和 b 的正负情况
a = 7;
b = -3;

remainder = a % b;
modulus = Math.floorMod(a, b);

System.out.println("\n数字: a = " + a + ", b = " + b);
System.out.println("取余 (%): " + remainder);
System.out.println("取模 (Math.floorMod): " + modulus);

输出结果如下所示：

数字: a = -7, b = 3
取余 (%): -1
取模 (Math.floorMod): 2

数字: a = 7, b = -3
取余 (%): 1
取模 (Math.floorMod): -2

为什么会有这样的结果呢？

首先，我们来考虑一下常规除法。当我们将一个数除以另一个数时，我们将得到一个商和一个余数。

例如，当我们把 7 除以 3 时，我们得到商 2 和余数 1，因为 (7 = 3 × 2 + 1)。

取模运算%和位运算&

可能大家在疑惑：取模运算难道不该用 % 吗？为什么要用位运算 & 呢？

这是因为 & 运算比 % 更加高效，并且当 b 为 2 的 n 次方时，存在下面这样一个公式。

a % b = a & (b-1)

用 ${2^n}$ 替换下 b 就是：

a % ${2^n}$ = a & (${2^n}$-1)

我们来验证一下，假如 a = 14，b = 8，也就是 ${2^3}$，n=3。

14%8（余数为 6）。

14 的二进制为 1110，8 的二进制 1000，8-1 = 7，7 的二进制为 0111，1110&0111=0110，也就是 0*${2^0}$+1*${2^1}$+1*${2^2}$+0*${2^3}$=0+2+4+0=6，14%8 刚好也等于 6。

害，计算机就是这么讲道理，没办法，😝

这也正好解释了为什么 HashMap 的数组长度要取 2 的整次方。

为什么会这样巧呢？

因为（数组长度-1）正好相当于一个“低位掩码”——这个掩码的低位最好全是 1，这样 & 操作才有意义，否则结果就肯定是 0。

a&b 操作的结果是：a、b 中对应位同时为 1，则对应结果位为 1，否则为 0。例如 5&3=1，5 的二进制是 0101，3 的二进制是 0011，5&3=0001=1。

2 的整次幂刚好是偶数，偶数-1 是奇数，奇数的二进制最后一位是 1，保证了 hash &(length-1) 的最后一位可能为 0，也可能为 1（取决于 hash 的值），即 & 运算后的结果可能为偶数，也可能为奇数，这样便可以保证哈希值的均匀分布。

换句话说，& 操作的结果就是将哈希值的高位全部归零，只保留低位值。

假设某哈希值的二进制为 10100101 11000100 00100101，用它来做 & 运算，我们来看一下结果。

我们知道，HashMap 的初始长度为 16，16-1=15，二进制是 00000000 00000000 00001111（高位用 0 来补齐）：

	 10100101 11000100 00100101
&	 00000000 00000000 00001111
----------------------------------
	 00000000 00000000 00000101

因为 15 的高位全部是 0，所以 & 运算后的高位结果肯定也是 0，只剩下 4 个低位 0101，也就是十进制的 5。

这样，哈希值为 10100101 11000100 00100101 的键就会放在数组的第 5 个位置上。

当然了，如果你是新手，上面这些 01 串看不太懂，也没关系。记住 &运算是为了计算数组的下标就可以了。

put 的时候计算下标，把键值对放到对应的桶上。
get 的时候通过下标，把键值对从对应的桶上取出来。

为什么取模运算之前要调用 hash 方法呢？

看下面这个图。

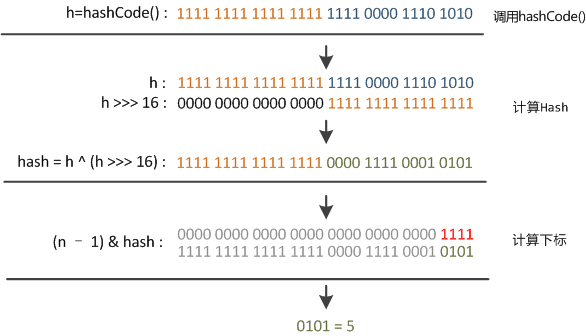
某哈希值为 11111111 11111111 11110000 1110 1010，将它右移 16 位（h >>> 16），刚好是 00000000 00000000 11111111 11111111，再进行异或操作（h ^ (h >>> 16)），结果是 11111111 11111111 00001111 00010101

异或（^）运算是基于二进制的位运算，采用符号 XOR 或者^来表示，运算规则是：如果是同值取 0、异值取 1

由于混合了原来哈希值的高位和低位，所以低位的随机性加大了（掺杂了部分高位的特征，高位的信息也得到了保留）。

结果再与数组长度-1（00000000 00000000 00000000 00001111）做取模运算，得到的下标就是 00000000 00000000 00000000 00000101，也就是 5。

还记得之前我们假设的某哈希值 10100101 11000100 00100101 吗？在没有调用 hash 方法之前，与 15 做取模运算后的结果也是 5，我们不妨来看看调用 hash 之后的取模运算结果是多少。

某哈希值 00000000 10100101 11000100 00100101（补齐 32 位），将它右移 16 位（h >>> 16），刚好是 00000000 00000000 00000000 10100101，再进行异或操作（h ^ (h >>> 16)），结果是 00000000 10100101 00111011 10000000

结果再与数组长度-1（00000000 00000000 00000000 00001111）做取模运算，得到的下标就是 00000000 00000000 00000000 00000000，也就是 0。

综上所述，hash 方法是用来做哈希值优化的，把哈希值右移 16 位，也就正好是自己长度的一半，之后与原哈希值做异或运算，这样就混合了原哈希值中的高位和低位，增大了随机性。

说白了，hash 方法就是为了增加随机性，让数据元素更加均衡的分布，减少碰撞。

我这里写了一段测试代码，假如 HashMap 的容量就是第一次扩容时候的 16，我在里面放了五个键值对，来看一下键的 hash 值（经过 hash() 方法计算后的哈希码）和索引（取模运算后）

HashMap<String, String> map = new HashMap<>();
map.put("chenmo", "沉默");
map.put("wanger", "王二");
map.put("chenqingyang", "陈清扬");
map.put("xiaozhuanling", "小转铃");
map.put("fangxiaowan", "方小婉");

// 遍历 HashMap
for (String key : map.keySet()) {
    int h, n = 16;
    int hash = (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    int i = (n - 1) & hash;
    // 打印 key 的 hash 值 和 索引 i
    System.out.println(key + "的hash值 : " + hash +" 的索引 : " + i);
}

输出结果如下所示：

xiaozhuanling的hash值 : 14597045 的索引 : 5
fangxiaowan的hash值 : -392727066 的索引 : 6
chenmo的hash值 : -1361556696 的索引 : 8
chenqingyang的hash值 : -613818743 的索引 : 9
wanger的hash值 : -795084437 的索引 : 11

也就是说，此时还没有发生哈希冲突，索引值都是比较均匀分布的，5、6、8、9、11，这其中的很大一部分功劳，就来自于 hash 方法。

小结

hash 方法的主要作用是将 key 的 hashCode 值进行处理，得到最终的哈希值。由于 key 的 hashCode 值是不确定的，可能会出现哈希冲突，因此需要将哈希值通过一定的算法映射到 HashMap 的实际存储位置上。

hash 方法的原理是，先获取 key 对象的 hashCode 值，然后将其高位与低位进行异或操作，得到一个新的哈希值。为什么要进行异或操作呢？因为对于 hashCode 的高位和低位，它们的分布是比较均匀的，如果只是简单地将它们加起来或者进行位运算，容易出现哈希冲突，而异或操作可以避免这个问题。

然后将新的哈希值取模（mod），得到一个实际的存储位置。这个取模操作的目的是将哈希值映射到桶（Bucket）的索引上，桶是 HashMap 中的一个数组，每个桶中会存储着一个链表（或者红黑树），装载哈希值相同的键值对（没有相同哈希值的话就只存储一个键值对）。

总的来说，HashMap 的 hash 方法就是将 key 对象的 hashCode 值进行处理，得到最终的哈希值，并通过一定的算法映射到实际的存储位置上。这个过程决定了 HashMap 内部键值对的查找效率。

02、HashMap 的扩容机制

好，理解了 hash 方法后我们来看第二个问题，HashMap 的扩容机制。

大家都知道，数组一旦初始化后大小就无法改变了，所以就有了 ArrayList这种“动态数组”，可以自动扩容。

HashMap 的底层用的也是数组。向 HashMap 里不停地添加元素，当数组无法装载更多元素时，就需要对数组进行扩容，以便装入更多的元素；除此之外，容量的提升也会相应地提高查询效率，因为“桶（坑）”更多了嘛，原来需要通过链表存储的（查询的时候需要遍历），扩容后可能就有自己专属的“坑位”了（直接就能查出来）。

来看这个例子，容量我们定位 16：

HashMap<String, String> map = new HashMap<>();
map.put("chenmo", "沉默");
map.put("wanger", "王二");
map.put("chenqingyang", "陈清扬");
map.put("xiaozhuanling", "小转铃");
map.put("fangxiaowan", "方小婉");
map.put("yexin", "叶辛");
map.put("liuting","刘婷");
map.put("yaoxiaojuan","姚小娟");

// 遍历 HashMap
for (String key : map.keySet()) {
    int h, n = 16;
    int hash = (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    int i = (n - 1) & hash;
    // 打印 key 的 hash 值 和 索引 i
    System.out.println(key + "的hash值 : " + hash +" 的索引 : " + i);
}

来看输出结果：

liuting的hash值 : 183821170 的索引 : 2
xiaozhuanling的hash值 : 14597045 的索引 : 5
fangxiaowan的hash值 : -392727066 的索引 : 6
yaoxiaojuan的hash值 : 1231568918 的索引 : 6
chenmo的hash值 : -1361556696 的索引 : 8
chenqingyang的hash值 : -613818743 的索引 : 9
yexin的hash值 : 114873289 的索引 : 9
wanger的hash值 : -795084437 的索引 : 11

看到没？

fangxiaowan（方小婉）和 yaoxiaojuan（姚小娟）的索引都是 6；
chenqingyang（陈清扬）和 yexin（叶辛）的索引都是 9

这就意味着，要采用拉链法（后面会讲）将他们放在同一个索引的链表上。查询的时候，就不能直接通过索引的方式直接拿到（时间复杂度为 O(1)），而要通过遍历的方式（时间复杂度为 O(n)）。

那假如把数组的长度由 16 扩容为 32 呢？

将之前示例中的 n 由 16 改为 32 即可得到如下的答案：

liuting的hash值 : 183821170 的索引 : 18
xiaozhuanling的hash值 : 14597045 的索引 : 21
fangxiaowan的hash值 : -392727066 的索引 : 6
yaoxiaojuan的hash值 : 1231568918 的索引 : 22
chenmo的hash值 : -1361556696 的索引 : 8
chenqingyang的hash值 : -613818743 的索引 : 9
yexin的hash值 : 114873289 的索引 : 9
wanger的hash值 : -795084437 的索引 : 11

可以看到：

虽然 chenqingyang（陈清扬）和 yexin（叶辛）的索引仍然是 9。
但 fangxiaowan（方小婉）的索引为 6，yaoxiaojuan（姚小娟）的索引由 6 变为 22，各自都有坑了。

当然了，数组是无法自动扩容的，所以如果要扩容的话，就需要新建一个大的数组，然后把之前小的数组的元素复制过去，并且要重新计算哈希值和重新分配桶（重新散列），这个过程也是挺耗时的。

resize 方法

HashMap 的扩容是通过 resize 方法来实现的，JDK 8 中融入了红黑树（链表长度超过 8 的时候，会将链表转化为红黑树来提高查询效率），对于新手来说，可能比较难理解。

为了减轻大家的学习压力，就还使用 JDK 7 的源码，搞清楚了 JDK 7 的，再看 JDK 8 的就会轻松很多。

来看 Java7 的 resize 方法源码，我加了注释：

// newCapacity为新的容量
void resize(int newCapacity) {
    // 小数组，临时过度下
    Entry[] oldTable = table;
    // 扩容前的容量
    int oldCapacity = oldTable.length;
    // MAXIMUM_CAPACITY 为最大容量，2 的 30 次方 = 1<<30
    if (oldCapacity == MAXIMUM_CAPACITY) {
        // 容量调整为 Integer 的最大值 0x7fffffff（十六进制）=2 的 31 次方-1
        threshold = Integer.MAX_VALUE;
        return;
    }

    // 初始化一个新的数组（大容量）
    Entry[] newTable = new Entry[newCapacity];
    // 把小数组的元素转移到大数组中
    transfer(newTable, initHashSeedAsNeeded(newCapacity));
    // 引用新的大数组
    table = newTable;
    // 重新计算阈值
    threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}

该方法接收一个新的容量 newCapacity，然后将 HashMap 的容量扩大到 newCapacity。

首先，方法获取当前 HashMap 的旧数组 oldTable 和旧容量 oldCapacity。如果旧容量已经达到 HashMap 支持的最大容量 MAXIMUM_CAPACITY（ 2 的 30 次方），就将新的阈值 threshold 调整为 Integer.MAX_VALUE（2 的 31 次方 - 1），这是因为 HashMap 的容量不能超过 MAXIMUM_CAPACITY。

因为 2,147,483,647（Integer.MAX_VALUE） - 1,073,741,824（MAXIMUM_CAPACITY） = 1,073,741,823，刚好相差一倍（HashMap 每次扩容都是之前的一倍）。

接着，方法创建一个新的数组 newTable，并将旧数组 oldTable 中的元素转移到新数组 newTable 中。转移过程是通过调用 transfer 方法来实现的。该方法遍历旧数组中的每个桶，并将每个桶中的键值对重新计算哈希值后，将其插入到新数组对应的桶中。

转移完成后，方法将 HashMap 内部的数组引用 table 指向新数组 newTable，并重新计算阈值 threshold。新的阈值是新容量 newCapacity 乘以负载因子 loadFactor 的结果，但如果计算结果超过了 HashMap 支持的最大容量 MAXIMUM_CAPACITY，则将阈值设置为 MAXIMUM_CAPACITY + 1，这是因为 HashMap 的元素数量不能超过 MAXIMUM_CAPACITY。

新容量 newCapacity

那 newCapacity 是如何计算的呢？

int newCapacity = oldCapacity * 2;
if (newCapacity < 0 || newCapacity >= MAXIMUM_CAPACITY) {
    newCapacity = MAXIMUM_CAPACITY;
} else if (newCapacity < DEFAULT_INITIAL_CAPACITY) {
    newCapacity = DEFAULT_INITIAL_CAPACITY;
}

新容量 newCapacity 被初始化为原容量 oldCapacity 的两倍。然后，如果 newCapacity 超过了 HashMap 的容量限制 MAXIMUM_CAPACITY（2^30），就将 newCapacity 设置为 MAXIMUM_CAPACITY。如果 newCapacity 小于默认初始容量 DEFAULT_INITIAL_CAPACITY（16），就将 newCapacity 设置为 DEFAULT_INITIAL_CAPACITY。这样可以避免新容量太小或太大导致哈希冲突过多或者浪费空间。

Java 8 的时候，newCapacity 的计算方式发生了一些细微的变化。

int newCapacity = oldCapacity << 1;
if (newCapacity >= DEFAULT_INITIAL_CAPACITY && oldCapacity >= DEFAULT_INITIAL_CAPACITY) {
    if (newCapacity > MAXIMUM_CAPACITY)
        newCapacity = MAXIMUM_CAPACITY;
} else {
    if (newCapacity < DEFAULT_INITIAL_CAPACITY)
        newCapacity = DEFAULT_INITIAL_CAPACITY;
}

注意，oldCapacity * 2 变成了 oldCapacity << 1，出现了左移（<<），这里简单介绍一下：

a=39
b = a << 2

十进制 39 用 8 位的二进制来表示，就是 00100111，左移两位后是 10011100（低位用 0 补上），再转成十进制数就是 156。

移位运算通常可以用来代替乘法运算和除法运算。例如，将 0010011（39）左移两位就是 10011100（156），刚好变成了原来的 4 倍。

实际上呢，二进制数左移后会变成原来的 2 倍、4 倍、8 倍，记住这个就好。

transfer 方法

接下来，来说 transfer 方法，该方法用来转移，将旧的小数组元素拷贝到新的大数组中。

void transfer(Entry[] newTable, boolean rehash) {
    // 新的容量
    int newCapacity = newTable.length;
    // 遍历小数组
    for (Entry<K,V> e : table) {
        while(null != e) {
            // 拉链法，相同 key 上的不同值
            Entry<K,V> next = e.next;
            // 是否需要重新计算 hash
            if (rehash) {
                e.hash = null == e.key ? 0 : hash(e.key);
            }
            // 根据大数组的容量，和键的 hash 计算元素在数组中的下标
            int i = indexFor(e.hash, newCapacity);

            // 同一位置上的新元素被放在链表的头部
            e.next = newTable[i];

            // 放在新的数组上
            newTable[i] = e;

            // 链表上的下一个元素
            e = next;
        }
    }
}

该方法接受一个新的 Entry 数组 newTable 和一个布尔值 rehash 作为参数，其中 newTable 表示新的哈希表，rehash 表示是否需要重新计算键的哈希值。

在方法中，首先获取新哈希表（数组）的长度 newCapacity，然后遍历旧哈希表中的每个 Entry。对于每个 Entry，使用拉链法将相同 key 值的不同 value 值存储在同一个链表中。如果 rehash 为 true，则需要重新计算键的哈希值，并将新的哈希值存储在 Entry 的 hash 属性中。

接着，根据新哈希表的长度和键的哈希值，计算 Entry 在新数组中的位置 i，然后将该 Entry 添加到新数组的 i 位置上。由于新元素需要被放在链表的头部，因此将新元素的下一个元素设置为当前数组位置上的元素。

最后，遍历完旧哈希表中的所有元素后，转移工作完成，新的哈希表 newTable 已经包含了旧哈希表中的所有元素。

拉链法

注意，e.next = newTable[i]，也就是使用了单链表的头插入方式，同一位置上新元素总会被放在链表的头部位置；这样先放在一个索引上的元素最终会被放到链表的尾部，这就会导致在旧数组中同一个链表上的元素，通过重新计算索引位置后，有可能被放到了新数组的不同位置上。

为了解决这个问题，Java 8 做了很大的优化（讲扩容的时候会讲到）。

Java 8 扩容

JDK 8 的扩容源代码：

final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table; // 获取原来的数组 table
    int oldCap = (oldTab == null) ? 0 : oldTab.length; // 获取数组长度 oldCap
    int oldThr = threshold; // 获取阈值 oldThr
    int newCap, newThr = 0;
    if (oldCap > 0) { // 如果原来的数组 table 不为空
        if (oldCap >= MAXIMUM_CAPACITY) { // 超过最大值就不再扩充了，就只好随你碰撞去吧
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && // 没超过最大值，就扩充为原来的2倍
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else { // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    // 计算新的 resize 上限
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr; // 将新阈值赋值给成员变量 threshold
    @SuppressWarnings({"rawtypes","unchecked"})
        Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; // 创建新数组 newTab
    table = newTab; // 将新数组 newTab 赋值给成员变量 table
    if (oldTab != null) { // 如果旧数组 oldTab 不为空
        for (int j = 0; j < oldCap; ++j) { // 遍历旧数组的每个元素
            Node<K,V> e;
            if ((e = oldTab[j]) != null) { // 如果该元素不为空
                oldTab[j] = null; // 将旧数组中该位置的元素置为 null，以便垃圾回收
                if (e.next == null) // 如果该元素没有冲突
                    newTab[e.hash & (newCap - 1)] = e; // 直接将该元素放入新数组
                else if (e instanceof TreeNode) // 如果该元素是树节点
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); // 将该树节点分裂成两个链表
                else { // 如果该元素是链表
                    Node<K,V> loHead = null, loTail = null; // 低位链表的头结点和尾结点
                    Node<K,V> hiHead = null, hiTail = null; // 高位链表的头结点和尾结点
                    Node<K,V> next;
                    do { // 遍历该链表
                        next = e.next;
                        if ((e.hash & oldCap) == 0) { // 如果该元素在低位链表中
                            if (loTail == null) // 如果低位链表还没有结点
                                loHead = e; // 将该元素作为低位链表的头结点
                            else
                                loTail.next = e; // 如果低位链表已经有结点，将该元素加入低位链表的尾部
                            loTail = e; // 更新低位链表的尾结点
                        }
                        else { // 如果该元素在高位链表中
                            if (hiTail == null) // 如果高位链表还没有结点
                                hiHead = e; // 将该元素作为高位链表的头结点
                            else
                                hiTail.next = e; // 如果高位链表已经有结点，将该元素加入高位链表的尾部
                            hiTail = e; // 更新高位链表的尾结点
                        }
                    } while ((e = next) != null); //
                    if (loTail != null) { // 如果低位链表不为空
                        loTail.next = null; // 将低位链表的尾结点指向 null，以便垃圾回收
                        newTab[j] = loHead; // 将低位链表作为新数组对应位置的元素
                    }
                    if (hiTail != null) { // 如果高位链表不为空
                        hiTail.next = null; // 将高位链表的尾结点指向 null，以便垃圾回收
                        newTab[j + oldCap] = hiHead; // 将高位链表作为新数组对应位置的元素
                    }
                }
            }
        }
    }
    return newTab; // 返回新数组
}

1、获取原来的数组 table、数组长度 oldCap 和阈值 oldThr。

2、如果原来的数组 table 不为空，则根据扩容规则计算新数组长度 newCap 和新阈值 newThr，然后将原数组中的元素复制到新数组中。

3、如果原来的数组 table 为空但阈值 oldThr 不为零，则说明是通过带参数构造方法创建的 HashMap，此时将阈值作为新数组长度 newCap。

4、如果原来的数组 table 和阈值 oldThr 都为零，则说明是通过无参数构造方法创建的 HashMap，此时将默认初始容量 DEFAULT_INITIAL_CAPACITY（16）和默认负载因子 DEFAULT_LOAD_FACTOR（0.75）计算出新数组长度 newCap 和新阈值 newThr。

5、计算新阈值 threshold，并将其赋值给成员变量 threshold。

6、创建新数组 newTab，并将其赋值给成员变量 table。

7、如果旧数组 oldTab 不为空，则遍历旧数组的每个元素，将其复制到新数组中。

8、返回新数组 newTab。

在 JDK 7 中，定位元素位置的代码是这样的：

static int indexFor(int h, int length) {
    // assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";
    return h & (length-1);
}

其实就相当于用键的哈希值和数组大小取模，也就是 hashCode % table.length。

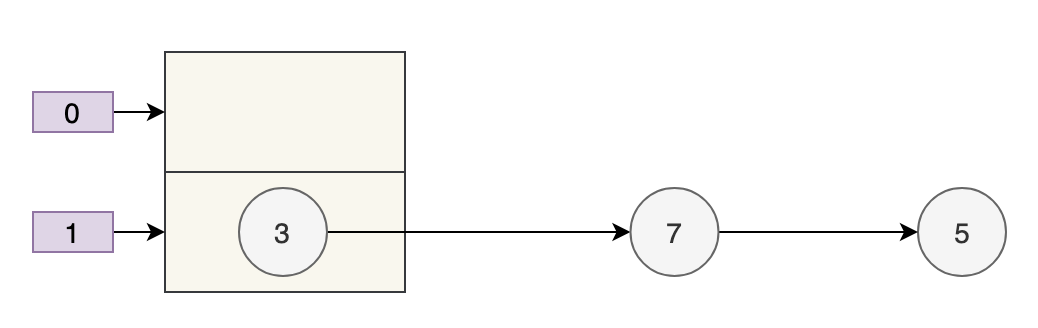
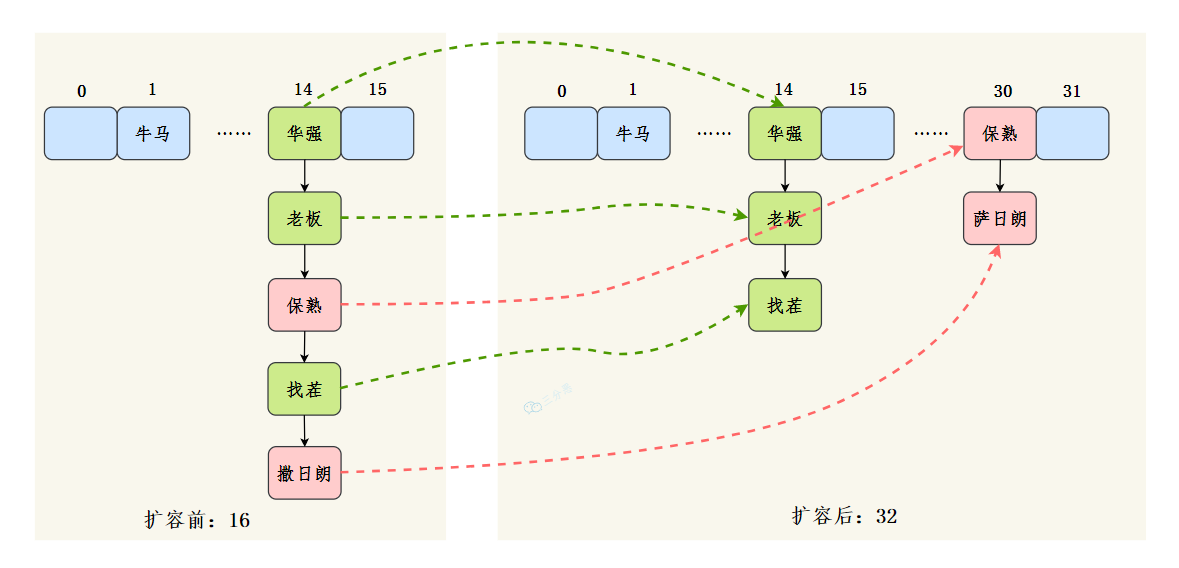
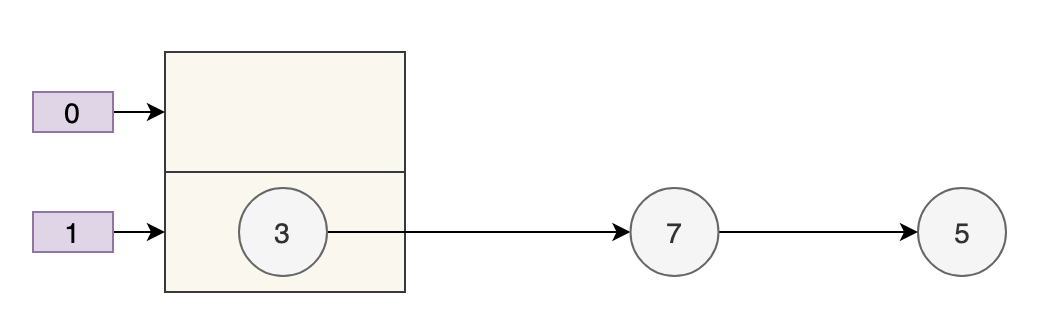
那我们来假设：

数组 table 的长度为 2
键的哈希值为 3、7、5

取模运算后，键发生了哈希冲突，都到 table[1] 上了。那么扩容前就是这个样子。

数组的容量为 2，key 为 3、7、5 的元素在 table[1] 上，需要通过拉链法来解决哈希冲突。

假设负载因子 loadFactor 为 1，也就是当元素的个数大于 table 的长度时进行扩容。

扩容后的数组容量为 4。

key 3 取模（3%4）后是 3，放在 table[3] 上。
key 7 取模（7%4）后是 3，放在 table[3] 上的链表头部。
key 5 取模（5%4）后是 1，放在 table[1] 上。

7 跑到 3 的前面了，因为 JDK 7 使用的是头插法。

e.next = newTable[i];

同时，扩容后的 5 跑到了下标为 1 的位置。

最好的情况就是，扩容后的 7 在 3 的后面，5 在 7 的后面，保持原来的顺序。

JDK 8 完全扭转了这个局面，因为 JDK 8 的哈希算法进行了优化，当数组长度为 2 的幂次方时，能够很巧妙地解决 JDK 7 中遇到的问题。

JDK 8 的扩容代码如下所示：

Node<K,V>[] newTab = new Node[newCapacity];
for (int j = 0; j < oldTab.length; j++) {
    Node<K,V> e = oldTab[j];
    if (e != null) {
        int hash = e.hash;
        int newIndex = hash & (newCapacity - 1); // 计算在新数组中的位置
        // 将节点移动到新数组的对应位置
        newTab[newIndex] = e;
    }
}

新索引的计算方式是 hash & (newCapacity - 1)，和 JDK 7 的 h & (length-1)没什么大的差别，差别主要在 hash 方法上，JDK 8 是这样：

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

过将键的hashCode()返回的 32 位哈希值与这个哈希值无符号右移 16 位的结果进行异或。

JDK 7 是这样：

final int hash(Object k) {
    int h = hashSeed;
    if (0 != h && k instanceof String) {
        return sun.misc.Hashing.stringHash32((String) k);
    }

    h ^= k.hashCode();

    // This function ensures that hashCodes that differ only by
    // constant multiples at each bit position have a bounded
    // number of collisions (approximately 8 at default load factor).
    h ^= (h >>> 20) ^ (h >>> 12);
    return h ^ (h >>> 7) ^ (h >>> 4);
}

我们用 JDK 8 的哈希算法来计算一下哈希值，就会发现别有洞天。

假设扩容前的数组长度为 16（n-1 也就是二进制的 0000 1111，1X$2^0$+1X$2^1$+1X$2^2$+1X$2^3$=1+2+4+8=15），key1 为 5（二进制为 0000 0101），key2 为 21（二进制为 0001 0101）。

key1 和 n-1 做 & 运算后为 0000 0101，也就是 5；
key2 和 n-1 做 & 运算后为 0000 0101，也就是 5。
此时哈希冲突了，用拉链法来解决哈希冲突。

现在，HashMap 进行了扩容，容量为原来的 2 倍，也就是 32（n-1 也就是二进制的 0001 1111，1X$2^0$+1X$2^1$+1X$2^2$+1X$2^3$+1X$2^4$=1+2+4+8+16=31）。

key1 和 n-1 做 & 运算后为 0000 0101，也就是 5；
key2 和 n-1 做 & 运算后为 0001 0101，也就是 21=5+16，也就是数组扩容前的位置+原数组的长度。

神奇吧？

也就是说，在 JDK 8 的新 hash 算法下，数组扩容后的索引位置，要么就是原来的索引位置，要么就是“原索引+原来的容量”，遵循一定的规律。

当然了，这个功劳既属于新的哈希算法，也离不开 n 为 2 的整数次幂这个前提，这是它俩通力合作后的结果 hash & (newCapacity - 1)。

小结

当我们往 HashMap 中不断添加元素时，HashMap 会自动进行扩容操作（条件是元素数量达到负载因子（load factor）乘以数组长度时），以保证其存储的元素数量不会超出其容量限制。

在进行扩容操作时，HashMap 会先将数组的长度扩大一倍，然后将原来的元素重新散列到新的数组中。

由于元素的位置是通过 key 的 hash 和数组长度进行与运算得到的，因此在数组长度扩大后，元素的位置也会发生一些改变。一部分索引不变，另一部分索引为“原索引+旧容量”。

03、加载因子为什么是 0.75

上一个问题提到了加载因子（或者叫负载因子），那么这个问题我们来讨论为什么加载因子是 0.75 而不是 0.6、0.8。

我们知道，HashMap 是用数组+链表/红黑树实现的，我们要想往 HashMap 中添加数据（元素/键值对）或者取数据，就需要确定数据在数组中的下标（索引）。

先把数据的键进行一次 hash：

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

再做一次取模运算确定下标：

i = (n - 1) & hash

那这样的过程容易产生两个问题：

数组的容量过小，经过哈希计算后的下标，容易出现冲突；
数组的容量过大，导致空间利用率不高。

加载因子是用来表示 HashMap 中数据的填满程度：

加载因子 = 填入哈希表中的数据个数 / 哈希表的长度

这就意味着：

加载因子越小，填满的数据就越少，哈希冲突的几率就减少了，但浪费了空间，而且还会提高扩容的触发几率；
加载因子越大，填满的数据就越多，空间利用率就高，但哈希冲突的几率就变大了。

好难！！！！

这就必须在“哈希冲突”与“空间利用率”两者之间有所取舍，尽量保持平衡，谁也不碍着谁。

我们知道，HashMap 是通过拉链法来解决哈希冲突的。

为了减少哈希冲突发生的概率，当 HashMap 的数组长度达到一个临界值的时候，就会触发扩容，扩容后会将之前小数组中的元素转移到大数组中，这是一个相当耗时的操作。

这个临界值由什么来确定呢？

临界值 = 初始容量 * 加载因子

一开始，HashMap 的容量是 16：

static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

加载因子是 0.75：

static final float DEFAULT_LOAD_FACTOR = 0.75f;

也就是说，当 16*0.75=12 时，会触发扩容机制。

为什么加载因子会选择 0.75 呢？为什么不是 0.8、0.6 呢？

这跟统计学里的一个很重要的原理——泊松分布有关。

是时候上维基百科了：

泊松分布，是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松在 1838 年时提出。它会对随机事件的发生次数进行建模，适用于涉及计算在给定的时间段、距离、面积等范围内发生随机事件的次数的应用情形。

阮一峰老师曾在一篇博文中详细的介绍了泊松分布和指数分布，大家可以去看一下。

链接：https://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html

具体是用这么一个公式来表示的。

等号的左边，P 表示概率，N 表示某种函数关系，t 表示时间，n 表示数量。

在 HashMap 的 doc 文档里，曾有这么一段描述：

Because TreeNodes are about twice the size of regular nodes, we
use them only when bins contain enough nodes to warrant use
(see TREEIFY_THRESHOLD). And when they become too small (due to
removal or resizing) they are converted back to plain bins.  In
usages with well-distributed user hashCodes, tree bins are
rarely used.  Ideally, under random hashCodes, the frequency of
nodes in bins follows a Poisson distribution
(http://en.wikipedia.org/wiki/Poisson_distribution) with a
parameter of about 0.5 on average for the default resizing
threshold of 0.75, although with a large variance because of
resizing granularity. Ignoring variance, the expected
occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
factorial(k)). The first values are:
0:    0.60653066
1:    0.30326533
2:    0.07581633
3:    0.01263606
4:    0.00157952
5:    0.00015795
6:    0.00001316
7:    0.00000094
8:    0.00000006
more: less than 1 in ten million

为了便于大家的理解，这里来重温一下 HashMap 的拉链法和红黑树结构。

Java 8 之前，HashMap 使用链表来解决冲突，即当两个或者多个键映射到同一个桶时，它们被放在同一个桶的链表上。当链表上的节点（Node）过多时，链表会变得很长，查找的效率（LinkedList 的查找效率为 O（n））就会受到影响。

Java 8 中，当链表的节点数超过一个阈值（8）时，链表将转为红黑树（节点为 TreeNode），红黑树（在讲TreeMap时会细说）是一种高效的平衡树结构，能够在 O(log n) 的时间内完成插入、删除和查找等操作。这种结构在节点数很多时，可以提高 HashMap 的性能和可伸缩性。

好，有了这个背景，我们来把上面的 doc 文档翻译为中文：

因为TreeNode（红黑树的节点）的大小大约是常规节点（链表的节点 Node）的两倍，所以只有当桶内包含足够多的节点时才使用红黑树（参见TREEIFY_THRESHOLD「阈值，值为8」，节点数量较多时，红黑树可以提高查询效率）。

由于删除元素或者调整数组大小（扩容）时（再次散列），红黑树可能会被转换为链表（节点数量小于 8 时），节点数量较少时，链表的效率比红黑树更高，因为红黑树需要更多的内存空间来存储节点。

在具有良好分布的hashCode使用中，很少使用红黑树。

理想情况下，在随机hashCode下，节点在桶中的频率遵循泊松分布（https://zh.wikipedia.org/wiki/卜瓦松分布），平均缩放阈值为0.75，忽略方差，列表大小k的预期出现次数为（exp（-0.5）* pow（0.5，k）/ factorial（k））。

前几个值是：
0: 0.60653066
1: 0.30326533
2: 0.07581633
3: 0.01263606
4: 0.00157952
5: 0.00015795
6: 0.00001316
7: 0.00000094
8: 0.00000006

更多：小于一千万分之一

虽然这段话的本意更多的是表示 jdk 8 中为什么拉链长度超过 8 的时候进行了红黑树转换，但提到了 0.75 这个加载因子，但没提到底为什么。

为了搞清楚到底为什么，我看到了这篇文章：

参考链接：https://segmentfault.com/a/1190000023308658

里面提到了一个概念：二项分布（Binomial Distribution）。

在做一件事情的时候，其结果的概率只有 2 种情况，和抛硬币一样，不是正面就是反面。

假如，我们做了 N 次实验，那么在每次试验中只有两种可能的结果，并且每次实验是独立的，不同实验之间互不影响，每次实验成功的概率都是一样的。

以此理论为基础：我们往哈希表中扔数据，如果发生哈希冲突就为失败，否则为成功。

我们可以设想，实验的 hash 值是随机的，并且经过 hash 运算的键都会映射到 hash 表的地址空间上，那么这个结果也是随机的。所以，每次 put 的时候就相当于我们在扔一个 16 面（HashMap 第一次扩容后的数组默认长度为 16）的骰子，扔骰子实验那肯定是相互独立的。碰撞发生即扔了 n 次有出现重复数字。

然后，我们的目的是啥呢？

就是掷了 k 次骰子，没有一次是相同的概率，需要尽可能的大些，一般意义上我们肯定要大于 0.5（这个数是个理想数）。

于是，n 次事件里面，碰撞为 0 的概率，由上面公式得：

这个概率值需要大于 0.5，我们认为这样的 hashmap 可以提供很低的碰撞率。所以：

这时候，我们对于该公式其实最想求的时候长度 s 的时候，n 为多少次就应该进行扩容了？而负载因子则是$n/s$的值。所以推导如下：

所以可以得到

其中

这就是一个求 ∞⋅0函数极限问题，这里我们先令$s = m+1（m \to \infty）$则转化为

我们再令 $x = \frac{1}{m} （x \to 0）$ 则有，

所以

考虑到 HashMap 的容量有一个要求：它必须是 2 的 n 次幂。当加载因子选择了 0.75 就可以保证它与容量的乘积为整数。

16*0.75=12
32*0.75=24

除了 0.75，0.5~1 之间还有 0.625（5/8）、0.875（7/8）可选，从中位数的角度，挑 0.75 比较完美。另外，维基百科上说，拉链法（解决哈希冲突的一种）的加载因子最好限制在 0.7-0.8 以下，超过 0.8，查表时的 CPU 缓存不命中（cache missing）会按照指数曲线上升。

综上，0.75 是个比较完美的选择。

小结

HashMap 的加载因子（load factor，直译为加载因子，意译为负载因子）是指哈希表中填充元素的个数与桶的数量的比值，当元素个数达到负载因子与桶的数量的乘积时，就需要进行扩容。这个值一般选择 0.75，是因为这个值可以在时间和空间成本之间做到一个折中，使得哈希表的性能达到较好的表现。

如果负载因子过大，填充因子较多，那么哈希表中的元素就会越来越多地聚集在少数的桶中，这就导致了冲突的增加，这些冲突会导致查找、插入和删除操作的效率下降。同时，这也会导致需要更频繁地进行扩容，进一步降低了性能。

如果负载因子过小，那么桶的数量会很多，虽然可以减少冲突，但是在空间利用上面也会有浪费，因此选择 0.75 是为了取得一个平衡点，即在时间和空间成本之间取得一个比较好的平衡点。

总之，选择 0.75 这个值是为了在时间和空间成本之间达到一个较好的平衡点，既可以保证哈希表的性能表现，又能够充分利用空间。

04、线程不安全

其实这个问题也不用说太多，但考虑到面试的时候有些面试官会问，那就简单说一下。

三方面原因：

多线程下扩容会死循环
多线程下 put 会导致元素丢失
put 和 get 并发时会导致 get 到 null

1）多线程下扩容会死循环

众所周知，HashMap 是通过拉链法来解决哈希冲突的，也就是当哈希冲突时，会将相同哈希值的键值对通过链表的形式存放起来。

JDK 7 时，采用的是头部插入的方式来存放链表的，也就是下一个冲突的键值对会放在上一个键值对的前面（讲扩容的时候讲过了）。扩容的时候就有可能导致出现环形链表，造成死循环。

resize 方法的源码：

// newCapacity为新的容量
void resize(int newCapacity) {
    // 小数组，临时过度下
    Entry[] oldTable = table;
    // 扩容前的容量
    int oldCapacity = oldTable.length;
    // MAXIMUM_CAPACITY 为最大容量，2 的 30 次方 = 1<<30
    if (oldCapacity == MAXIMUM_CAPACITY) {
        // 容量调整为 Integer 的最大值 0x7fffffff（十六进制）=2 的 31 次方-1
        threshold = Integer.MAX_VALUE;
        return;
    }

    // 初始化一个新的数组（大容量）
    Entry[] newTable = new Entry[newCapacity];
    // 把小数组的元素转移到大数组中
    transfer(newTable, initHashSeedAsNeeded(newCapacity));
    // 引用新的大数组
    table = newTable;
    // 重新计算阈值
    threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}

transfer 方法用来转移，将小数组的元素拷贝到新的数组中。

void transfer(Entry[] newTable, boolean rehash) {
    // 新的容量
    int newCapacity = newTable.length;
    // 遍历小数组
    for (Entry<K,V> e : table) {
        while(null != e) {
            // 拉链法，相同 key 上的不同值
            Entry<K,V> next = e.next;
            // 是否需要重新计算 hash
            if (rehash) {
                e.hash = null == e.key ? 0 : hash(e.key);
            }
            // 根据大数组的容量，和键的 hash 计算元素在数组中的下标
            int i = indexFor(e.hash, newCapacity);

            // 同一位置上的新元素被放在链表的头部
            e.next = newTable[i];

            // 放在新的数组上
            newTable[i] = e;

            // 链表上的下一个元素
            e = next;
        }
    }
}

注意 e.next = newTable[i] 和 newTable[i] = e 这两行代码，它们会将同一位置上的新元素放在链表的头部。

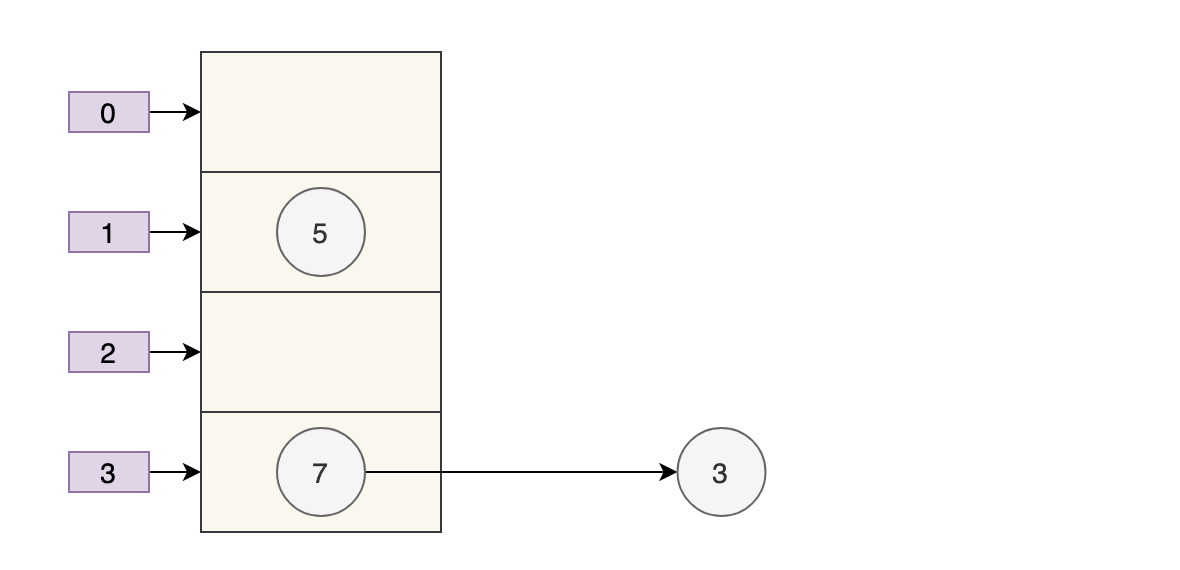
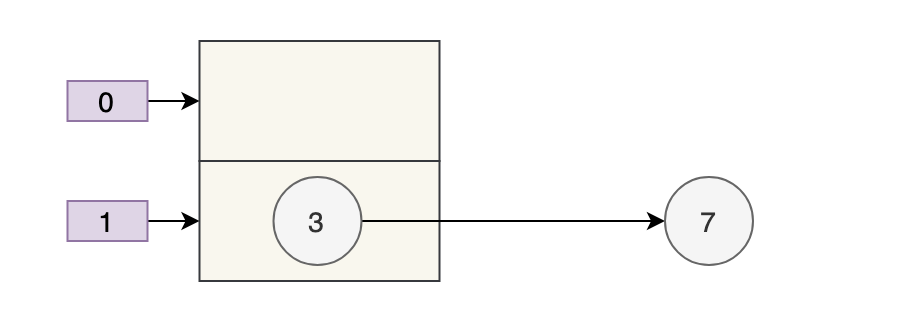
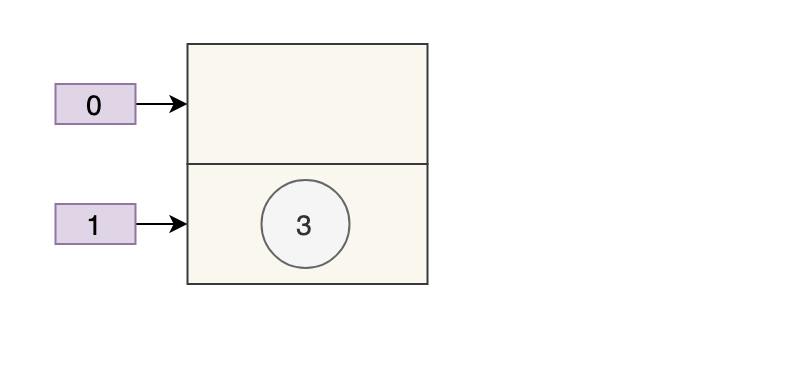
扩容前的样子假如是下面这样子。

那么正常扩容后就是下面这样子。

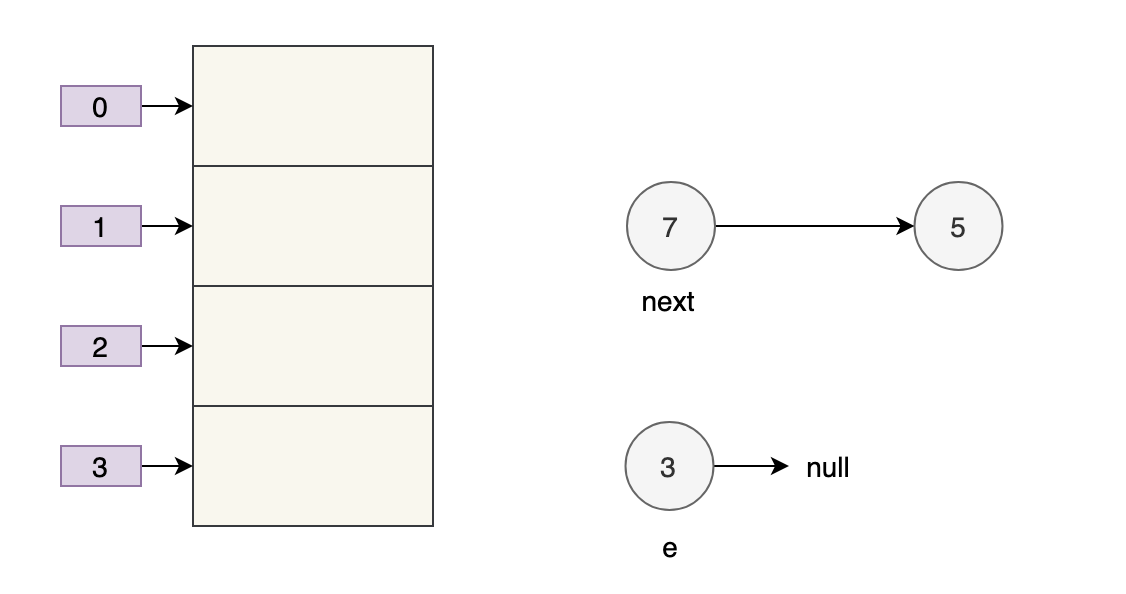
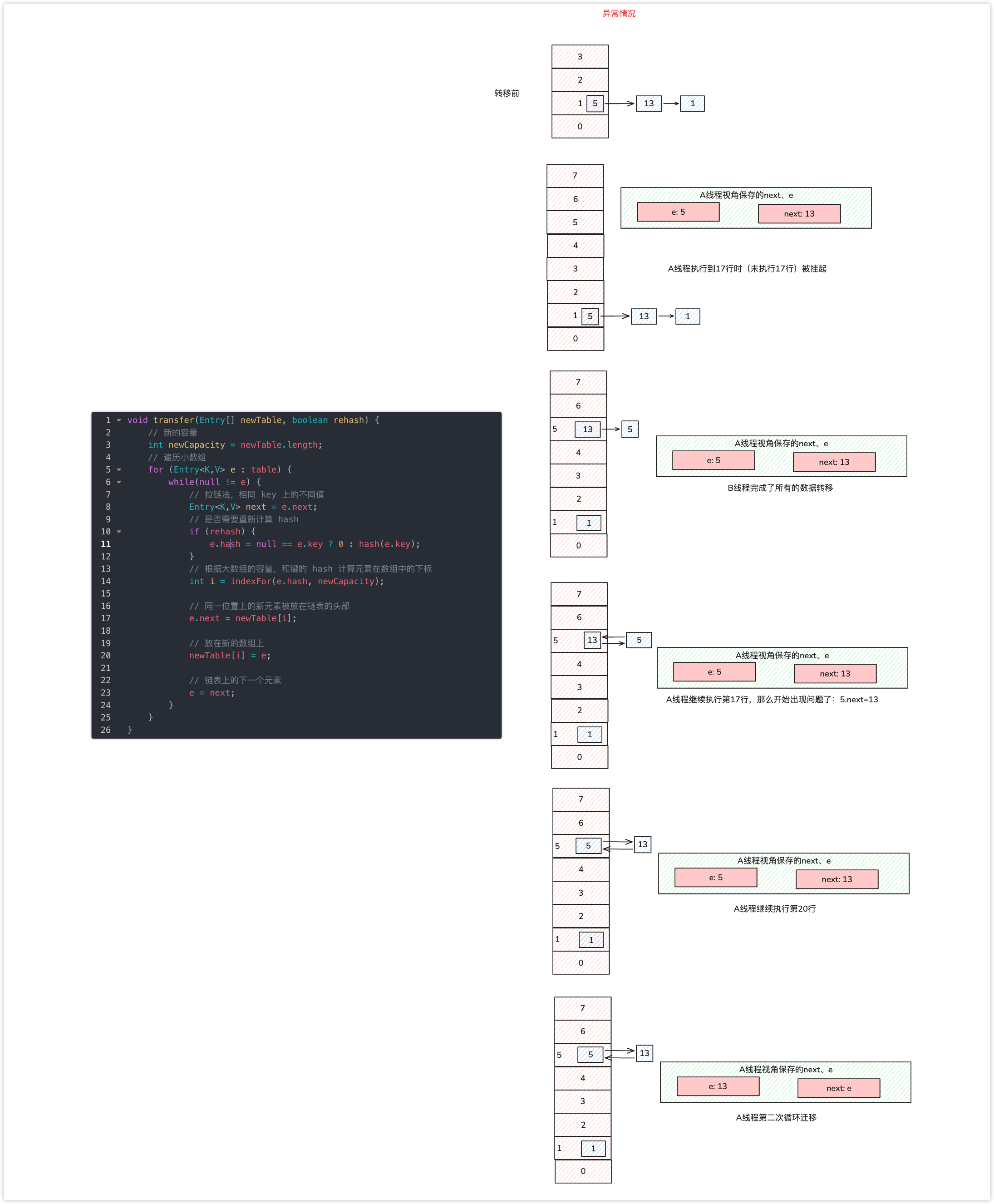
假设现在有两个线程同时进行扩容，线程 A 在执行到 e.next = newTable[i] 被挂起，此时线程 A 中：e=3、next=7、e.next=null

线程 B 开始执行，并且完成了数据转移。

此时，7 的 next 为 3，3 的 next 为 null。

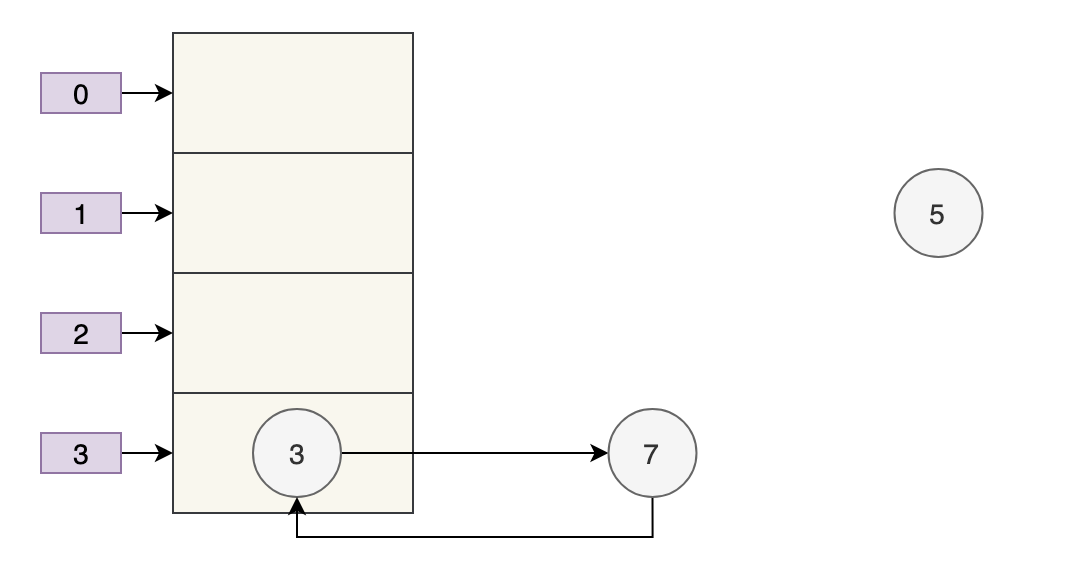
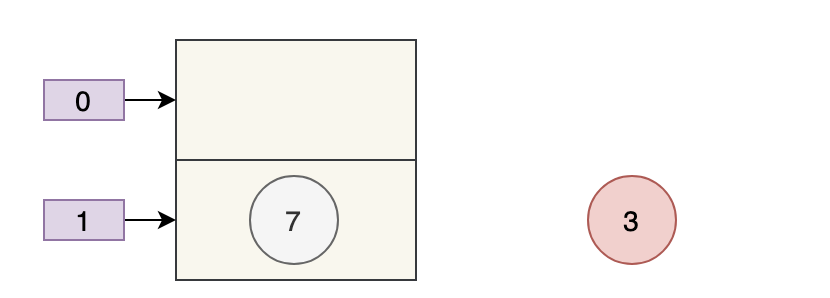
随后线程 A 获得 CPU 时间片继续执行 e.next = newTable[i];newTable[i] = e，将 3 放入新数组对应的位置，执行完此轮循环后线程 A 的情况如下：

执行下一轮循环，此时 e=7，原本线程 A 中 7 的 next 为 5，但由于 table 是线程 A 和线程 B 共享的，而线程 B 顺利执行完后，7 的 next 变成了 3，那么此时线程 A 中，7 的 next 也为 3 了。

采用头部插入的方式，变成了下面这样子：

好像也没什么问题，此时 next = 3，e = 3。

进行下一轮循环，但此时，由于线程 B 将 3 的 next 变为了 null，所以此轮循环应该是最后一轮了。

接下来当执行完 e.next=newTable[i] 即 3.next=7 后，3 和 7 之间就相互链接了，执行完 newTable[i]=e 后，3 被头插法重新插入到链表中，执行结果如下图所示：

套娃开始，元素 5 也就成了弃婴，惨~~~

这里再插入一名球友小灰飞的分析：“线程A是在8行之后、17行之前挂起”。

不过，JDK 8 时已经修复了这个问题，扩容时会保持链表原来的顺序（嗯，等于说了半天白说了，哈哈，这个面试题确实是这样，很水，但有些面试官又确实比较装逼）。

2）多线程下 put 会导致元素丢失

正常情况下，当发生哈希冲突时，HashMap 是这样的：

但多线程同时执行 put 操作时，如果计算出来的索引位置是相同的，那会造成前一个 key 被后一个 key 覆盖，从而导致元素的丢失。

put 的源码：

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;

    // 步骤①：tab为空则创建
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;

    // 步骤②：计算index，并对null做处理
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K,V> e; K k;

        // 步骤③：节点key存在，直接覆盖value
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;

        // 步骤④：判断该链为红黑树
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);

        // 步骤⑤：该链为链表
        else {
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);

                    //链表长度大于8转换为红黑树进行处理
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }

                // key已经存在直接覆盖value
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }

        // 步骤⑥、直接覆盖
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;

    // 步骤⑦：超过最大容量 就扩容
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

问题发生在步骤 ② 这里：

if ((p = tab[i = (n - 1) & hash]) == null)
    tab[i] = newNode(hash, key, value, null);

两个线程都执行了 if 语句，假设线程 A 先执行了 tab[i] = newNode(hash, key, value, null)，那 table 是这样的：

接着，线程 B 执行了 tab[i] = newNode(hash, key, value, null)，那 table 是这样的：

3 被干掉了。

3）put 和 get 并发时会导致 get 到 null

线程 1 执行 put 时，因为元素个数超出阈值而导致出现扩容，线程 2 此时执行 get，就有可能出现这个问题。

因为线程 1 执行完 table = newTab 之后，线程 2 中的 table 此时也发生了变化，此时去 get 的时候当然会 get 到 null 了，因为元素还没有转移。

参考链接：

https://blog.csdn.net/lonyw/article/details/80519652

https://zhuanlan.zhihu.com/p/91636401

https://www.zhihu.com/question/20733617

https://zhuanlan.zhihu.com/p/21673805

4）小结

HashMap 是线程不安全的主要是因为它在进行插入、删除和扩容等操作时可能会导致链表的结构发生变化，从而破坏了 HashMap 的不变性。具体来说，如果在一个线程正在遍历 HashMap 的链表时，另外一个线程对该链表进行了修改（比如添加了一个节点），那么就会导致链表的结构发生变化，从而破坏了当前线程正在进行的遍历操作，可能导致遍历失败或者出现死循环等问题。

为了解决这个问题，Java 提供了线程安全的 HashMap 实现类 ConcurrentHashMap。ConcurrentHashMap 内部采用了分段锁（Segment），将整个 Map 拆分为多个小的 HashMap，每个小的 HashMap 都有自己的锁，不同的线程可以同时访问不同的小 Map，从而实现了线程安全。在进行插入、删除和扩容等操作时，只需要锁住当前小 Map，不会对整个 Map 进行锁定，提高了并发访问的效率。

05、小结

HashMap 是 Java 中最常用的集合之一，它是一种键值对存储的数据结构，可以根据键来快速访问对应的值。以下是对 HashMap 的总结：

HashMap 采用数组+链表/红黑树的存储结构，能够在 O(1)的时间复杂度内实现元素的添加、删除、查找等操作。
HashMap 是线程不安全的，因此在多线程环境下需要使用ConcurrentHashMap来保证线程安全。
HashMap 的扩容机制是通过扩大数组容量和重新计算 hash 值来实现的，扩容时需要重新计算所有元素的 hash 值，因此在元素较多时扩容会影响性能。
在 Java 8 中，HashMap 的实现引入了拉链法、树化等机制来优化大量元素存储的情况，进一步提升了性能。
HashMap 中的 key 是唯一的，如果要存储重复的 key，则后面的值会覆盖前面的值。
HashMap 的初始容量和加载因子都可以设置，初始容量表示数组的初始大小，加载因子表示数组的填充因子。一般情况下，初始容量为 16，加载因子为 0.75。
HashMap 在遍历时是无序的，因此如果需要有序遍历，可以使用TreeMap。

综上所述，HashMap 是一种高效的数据结构，具有快速查找和插入元素的能力，但需要注意线程安全和性能问题。

那如果大家已经掌握了 HashMap，那可以刷一下 LeetCode 的第 001 题、013 题，会用到 HashMap、数组和 for 循环，我把题解链接放在了技术派上：

二哥的 LeetCode 刷题笔记：001.两数之和

二哥的 LeetCode 刷题笔记：013.罗马数字转整数

另外，感谢球友踏歌对文章中的排版错误❎进行指正，文章已经进行了修改，感谢球友的支持。

GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了！包括 Java 基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM 等等，共计 32 万余字，500+张手绘图，可以说是通俗易懂、风趣幽默……详情戳：太赞了，GitHub 上标星 7600+ 的 Java 教程

微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二，回复 222 即可免费领取。

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

hashmap.md

hashmap.md

01、hash 方法的原理

hash 方法的作用

取模运算 VS 取余运算 VS 与运算

取模运算%和位运算&

为什么取模运算之前要调用 hash 方法呢？

小结

02、HashMap 的扩容机制

resize 方法

新容量 newCapacity

transfer 方法

拉链法

Java 8 扩容

小结

03、加载因子为什么是 0.75

小结

04、线程不安全

1）多线程下扩容会死循环

2）多线程下 put 会导致元素丢失

3）put 和 get 并发时会导致 get 到 null

4）小结

05、小结

Files

hashmap.md

Latest commit

History

hashmap.md

File metadata and controls

01、hash 方法的原理

hash 方法的作用

取模运算 VS 取余运算 VS 与运算

取模运算%和位运算&

为什么取模运算之前要调用 hash 方法呢？

小结

02、HashMap 的扩容机制

resize 方法

新容量 newCapacity

transfer 方法

拉链法

Java 8 扩容

小结

03、加载因子为什么是 0.75

小结

04、线程不安全

1）多线程下扩容会死循环

2）多线程下 put 会导致元素丢失

3）put 和 get 并发时会导致 get 到 null

4）小结

05、小结