Protecting APIs from abuse using sequence learning and variable order Markov chains

[innocces]

The original blog info

subject	content
title	Protecting APIs from abuse using sequence learning and variable order Markov chains
url	blog url
author	Peter Foster

[innocces]

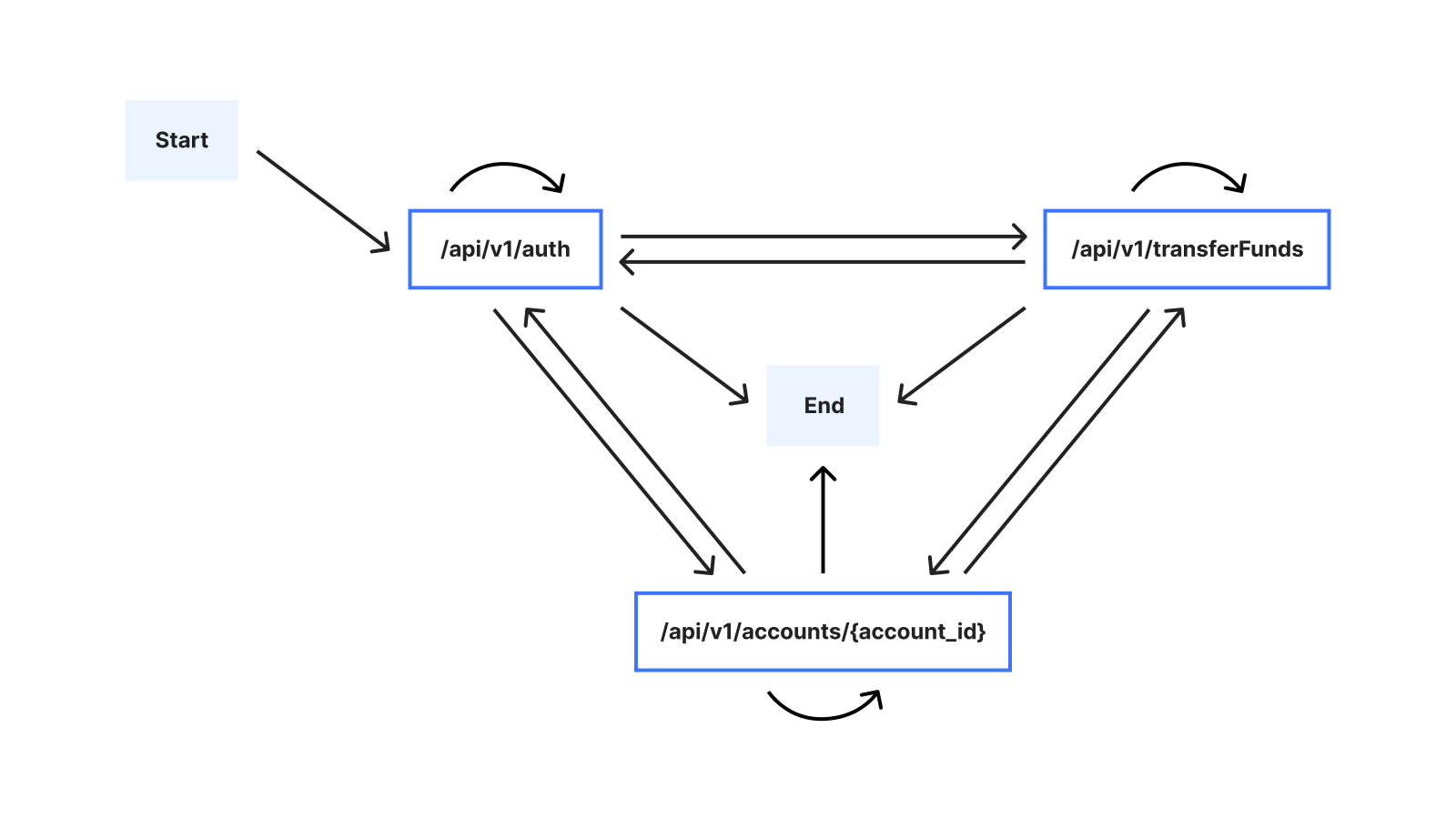
Protecting APIs from abuse using sequence learning and variable order Markov chains

2024-09-12

• 

  Peter Foster

10 min read

Consider the case of a malicious actor attempting to inject, scrape, harvest, or exfiltrate data via an API. Such malicious activities are often characterized by the particular order in which the actor initiates requests to API endpoints. Moreover, the malicious activity is often not readily detectable using volumetric techniques alone, because the actor may intentionally execute API requests slowly, in an attempt to thwart volumetric abuse protection. To reliably prevent such malicious activity, we therefore need to consider the sequential order of API requests. We use the term sequential abuse to refer to malicious API request behavior. Our fundamental goal thus involves distinguishing malicious from benign API request sequences.

In this blog post, you’ll learn about how we address the challenge of helping customers protect their APIs against sequential abuse. To this end, we’ll unmask the statistical machine learning (ML) techniques currently underpinning our Sequence Analytics product. We’ll build on the high-level introduction to Sequence Analytics provided in a previous blog post.

API sessions

Introduced in the previous blog post, let’s consider the idea of a time-ordered series of HTTP API requests initiated by a specific user. These occur as the user interacts with a service, such as while browsing a website or using a mobile app. We refer to the user’s time-ordered series of API requests as a session. Choosing a familiar example, the session for a customer interacting with a banking service might look like:

Time Order

Method

Path

Description

1

POST

/api/v1/auth

Authenticates a user

2

GET

/api/v1/accounts/{account_id}

Displays account balance, where account_id is an account belonging to the user

3

POST

/api/v1/transferFunds

Containing a request body detailing an account to transfer funds from, an account to transfer funds to, and an amount of money to transfer

One of our aims is to enable our customers to secure their APIs by automatically suggesting rules applicable to our Sequence Mitigation product for enforcing desired sequential behavior. If we enforce the expected behavior, we can prevent unwanted sequential behavior. In our example, desired sequential behavior might entail that /api/v1/auth must always precede /api/v1/accounts/{account_id}.

One important challenge we had to address is that the number of possible sessions grows rapidly as the session length increases. To see why, we can consider the alternative ways in which a user might interact with the example banking service: The user may, for example, execute multiple transfers, and/or check the balance of multiple accounts, in any order. Assuming that there are 3 possible endpoints, the following graph illustrates possible sessions when the user interacts with the banking service:

Because of this large number of possible sessions, suggesting mitigation rules requires that we address the challenge of summarizing sequential behavior from past session data as an intermediate step. We’ll refer to a series of consecutive endpoints in a session (for example /api/v1/accounts/{account_id} → /api/v1/transferFunds) in our example as a sequence. Specifically, a challenge we needed to address is that the sequential behavior relevant for creating rules isn’t necessarily apparent from volume alone: Consider for example that /api/transferFunds might nearly always be preceded by /api/v1/accounts/{account_id}, but also that the sequence /api/v1/accounts/{account_id} → /api/v1/transferFunds might occur relatively rarely, compared to the sequence /api/v1/auth → /api/v1/accounts/{account_id}. It is therefore conceivable that if we were to summarize based on volume alone, we might potentially deem the sequence /api/v1/accounts/{account_id} → /api/v1/transferFunds as unimportant, when in fact we ought to surface it as a potential rule. 

Learning important sequences from API sessions

A widely-applied modeling approach applicable to sequential data is the Markov chain, in which the probability of each endpoint in our session data depends only on a fixed number of preceding endpoints. First, we’ll show how standard Markov chains can be applied to our session data, while pointing out some of their limitations. Second, we’ll show how we use a less well-known, but powerful, type of Markov chain to determine important sequences.

For illustrative purposes, let’s assume that there are 3 possible endpoints in our session data. We’ll represent these endpoints using the letters a, b and c:

• a: /api/v1/auth

• b: /api/v1/accounts/{account_id}

• c: /api/v1/transferFunds

In its simplest form, a Markov chain is nothing more than a table which tells us the probability of the next letter, given knowledge of the immediately preceding letter. If we were to model past session data using the simplest kind of Markov chain, we might end up with a table like this one:

Known preceding endpoint in the session

Estimated probability of next endpoint in the session

a

b

c

a

0.10 (1555)

0.89 (13718)

0.01 (169)

b

0.03 (9618)

0.63 (205084)

0.35 (113382)

c

0.02 (3340)

0.67 (109896)

0.31 (51553)

Table 1

Table 1 lists the parameters of the Markov chain, namely the estimated probabilities of observing a, b or c as the next endpoint in a session, given knowledge of the immediately preceding endpoint in the session. For example, the 3rd row cell with value 0.67 means that given knowledge of immediately preceding endpoint c, the estimated probability of observing b as the next endpoint in a session is 67%, regardless of whether c was preceded by any endpoints. Thus, each entry in the table corresponds to a sequence of two endpoints. The values in brackets are the number of times we saw each two-endpoint sequence in past session data and are used to compute the probabilities in the table. For example, the value 0.01 is the result of evaluating the fraction 169 / (1555+13718+169). This method of estimating probabilities is known as maximum likelihood estimation.

To determine important sequences, we rely on credible intervals for estimating probabilities instead of maximum likelihood estimation. Instead of producing a single point estimate (as described above), credible intervals represent a plausible range of probabilities. This range reflects the amount of data available, i.e. the total number of sequence occurrences in each row. More data produces narrower credible intervals (reflecting a greater degree of certainty) and conversely less data produces wider credible intervals (reflecting a lesser degree of certainty). Based on the values in brackets in the table above, we thus might obtain the following credible intervals (entries in boldface will be explained further on):

Known preceding endpoint in the session

Estimated probability of next endpoint in the session

a

b

c

a

0.09-0.11 (1555)

0.88-0.89 (13718)

0.01-0.01 (169)

b

0.03-0.03 (9618)

0.62-0.63 (205084)

0.34-0.35 (113382)

c

0.02-0.02 (3340)

0.66-0.67 (109896)

0.31-0.32 (51553)

Table 2

For brevity, we won’t demonstrate here how to work out the credible intervals by hand (they involve evaluating the quantile function of a beta distribution). Notwithstanding, the revised table indicates how more data causes credible intervals to shrink: note the first row with a total of 15442 occurrences in comparison to the second row with a total of 328084 occurrences.

To determine important sequences, we use slightly more complex Markov chains than those described above. As an intermediate step, let’s first consider the case where each table entry corresponds to a sequence of 3 endpoints (instead of 2 as above), exemplified by the following table:

Known preceding endpoints in the session

Estimated probability of next endpoint in the session

a

b

c

aa

0.09-0.13 (173)

0.86-0.90 (1367)

0.00-0.02 (13)

ba

0.09-0.11 (940)

0.88-0.90 (8552)

0.01-0.01 (109)

ca

0.09-0.12 (357)

0.87-0.90 (2945)

0.01-0.02 (35)

ab

0.02-0.02 (272)

0.56-0.58 (7823)

0.40-0.42 (5604)

bb

0.03-0.03 (6067)

0.60-0.60 (122796)

0.37-0.37 (75801)

cb

0.03-0.03 (3279)

0.68-0.68 (74449)

0.29-0.29 (31960)

ac

0.01-0.09 (6)

0.77-0.91 (144)

0.06-0.19 (19)

bc

0.02-0.02 (2326)

0.77-0.77 (87215)

0.21-0.21 (23612)

cc

0.02-0.02 (1008)

0.43-0.44 (22527)

0.54-0.55 (27919)

Table 3

Table 3 again lists the estimated probabilities of observing a, b or c as the next endpoint in a session, but given knowledge of 2 immediately preceding endpoints in the session (instead of 1 immediately preceding endpoint as before). That is, the 3rd row cell with interval 0.09-0.13 means that given knowledge of immediately preceding endpoints ca, the probability of observing a as the next endpoint has a credible interval spanning 9% and 13%, regardless of whether ca was preceded by any endpoints. In parlance, we say that the above table represents a Markov chain of order 2. This is because the entries in the table represent probabilities of observing the next endpoint, given knowledge of 2 immediately preceding endpoints as context.

As a special case, the Markov chain of order 0 simply represents the distribution over endpoints in a session. We can tabulate the probabilities as follows, in relation to a single row corresponding to an ‘empty context’:

Known preceding endpoints in the session

Estimated probability of next endpoint in the session

a

b

c

0.03-0.03 (15466)

0.64-0.65 (328732)

0.32-0.33 (165117)

Table 4

Note that the probabilities in Table 4 do not solely represent the case where there were no preceding endpoints in the session. Rather, the probabilities are for the occurrence of endpoints in the session, for the general case where we have no knowledge of the preceding endpoints and regardless of how many endpoints previously occurred.    

Returning to our task of identifying important sequences, one possible approach might be to simply use a Markov chain of some fixed order N. For example, if we were to apply a threshold of 0.85 to the lower bounds of credible intervals in Table 3, we’d retain 3 sequences in total. On the other hand, this approach comes with two noteworthy limitations:

1. We need a way to select a suitable value for the model order N. 

2. Since the model order remains fixed, identified sequences all have the same length N+1.

Variable order Markov chains

Variable order Markov chains (VOMCs) are a more powerful extension of the described fixed-order Markov chains which address the preceding limitations. VOMCs make use of the fact that for some chosen value of the Markov chain of fixed order N, the probability table might include statistically redundant information: Let’s compare Tables 3 and 2 above and consider in Table 3 the rows in boldface corresponding to contexts aa, ba, ca (these 3 contexts all share _a_ as their suffix).

For all the 3 possible next endpoints a, b, c, these rows specify credible intervals which overlap with their respective estimates in Table 2 corresponding to context a (also indicated in boldface). We can interpret these overlapping intervals as representing no discernible difference between probability estimates, given knowledge of a as the preceding endpoint. With no discernible effect of what preceded a on the probability of the next endpoint, we can consider these 3 rows in Table 3 redundant: We may ‘collapse’ them by replacing them with the row in Table 2 corresponding to context a.

The result of revising Table 3 as described looks as follows (with the new row indicated in boldface):

Known preceding endpoints in the session

Estimated probability of next endpoint in the session

a

b

c

a

0.09-0.11 (1555)

0.88-0.89 (13718)

0.01-0.01 (169)

ab

0.02-0.02 (272)

0.56-0.58 (7823)

0.40-0.42 (5604)

ac

0.03-0.03 (6067)

0.60-0.60 (122796)

0.37-0.37 (75801)

bb

0.03-0.03 (3279)

0.68-0.68 (74449)

0.29-0.29 (31960)

bc

0.01-0.09 (6)

0.77-0.91 (144)

0.06-0.19 (19)

cb

0.02-0.02 (2326)

0.77-0.77 (87215)

0.21-0.21 (23612)

cc

0.02-0.02 (1008)

0.43-0.44 (22527)

0.54-0.55 (27919)

Table 5

Table 5 represents a VOMC, because the context length varies: In the example, we have context lengths 1 and 2. It follows that entries in the table represent sequences of length varying between 2 and 3 endpoints, depending on context length. Generalizing the described approach of collapsing contexts leads to the following algorithm sketch for learning a VOMC in an offline setting:

(1) Define the table _T_ containing the estimated probability of the next endpoint in a session, given alternatively _0, 1, 2, …, N_max_ preceding endpoints in the session. That is, form a single table by concatenating the rows corresponding to Markov chains of fixed orders _0, 1, 2, …, N_max_``.

(2) is_modified := true 

(3) DO WHILE is_modified

(4) _D_ := all contexts in _T_ which are not suffixes of at least 1 other context in _T_

(5) is_modified = false

(6) FOR _ctx_ IN _C_

(7) IF length(``_ctx_``) > 0

(8) _parent_ctx_ := the context obtained by deleting the leftmost endpoint in _ctx_

(9) IF is_collapsible(``_ctx_``, _parent_ctx_``)

(10) Modify _T_ by discarding _ctx_

(11) is_modified = true

In the pseudo-code, length(ctx) is the length of context ctx. On line 9, is_collapsible() involves comparing credible intervals for the contexts ctx and parent_ctx in the manner described for generating Table 5: is_collapsible() evaluates to true, if and only if we observe that all credible intervals overlap, when comparing contexts ctx and parent_ctx separately for each of the possible next endpoints. The maximum sequence length is N_max+1_,_ where N_max is some constant. On line 4, we say that context q is a suffix of another context p if we can form p by prepending zero or more endpoints to q. (According to this definition, the ‘empty context’ mentioned above for the order 0 model is a suffix of all contexts in T.) The above algorithm sketch is a variant of the ideas first introduced by Rissanen [1], Ron et al. [2].

Finally, we take the entries in the resulting table T as our important sequences. Thus, the result of applying VOMCs is a set of sequences that we deem important. For Sequence Analytics however, we believe that it is additionally useful to rank sequences. We do this by computing a ‘precedence score’ between 0.0 and 1.0, which is the number of occurrences of the sequence divided by the number of occurrences of the last endpoint in the sequence. Thus, precedence scores close to 1.0 indicate that a given endpoint is nearly always preceded by the remaining endpoints in the sequence. In this way, manual inspection of the highest-scoring sequences is a semi-automated heuristic for creating precedence rules in our Sequence Mitigation product.

Learning sequences at scale

The preceding represents a very high-level overview of the statistical ML techniques that we use in Sequence Analytics. In practice, we have devised an efficient algorithm which does not require an upfront training step, but rather updates the model continuously as the data arrive and generates a frequently-updating summary of important sequences. This approach allows us to overcome additional challenges around memory cost not touched on in this blog post. Most significantly, a straightforward implementation of the algorithm sketch above would still result in the number of table rows (contexts) exploding with increasing maximum sequence length. A further challenge we had to address is how to ensure that our system is able to deal with high-volume APIs, without adversely impacting CPU load. We use a horizontally scalable adaptive sampling strategy upfront, such that more aggressive sampling is applied to high-volume APIs. Our algorithm then consumes the sampled streams of API requests. After a customer onboards, sequences are assembled and learned over time, so that the current summary of important sequences represents a sliding window with a look-back interval of approximately 24 hours. Sequence Analytics further stores sequences in Clickhouse and exposes them via a GraphQL API and via the Cloudflare dashboard. Customers who would like to enforce sequence rules can do so using Sequence Mitigation. Sequence Mitigation is what is responsible for ensuring that rules are shared and matched in distributed fashion on Cloudflare’s global network — another exciting topic for a future blog post!

What’s next

Now that you have a better understanding of how we surface important API request sequences, stay tuned for a future blog post in this series, where we’ll describe how we find the anomalous API request sequences that customers may want to stop. For now, API Gateway customers can get started in two ways: with Sequence Analytics to explore important API request sequences and with Sequence Mitigation to enforce sequences of API requests. Enterprise customers that haven’t purchased API Gateway can get started by enabling the API Gateway trial inside the Cloudflare Dashboard or contacting their account manager.

Cloudflare's connectivity cloud protects entire corporate networks, helps customers build Internet-scale applications efficiently, accelerates any website or Internet application, wards off DDoS attacks, keeps hackers at bay, and can help you on your journey to Zero Trust.

Visit 1.1.1.1 from any device to get started with our free app that makes your Internet faster and safer.

To learn more about our mission to help build a better Internet, start here. If you're looking for a new career direction, check out our open positions.

[innocces]

使用序列学习和可变阶马尔可夫链保护 API 免遭滥用

2024-09-12

• 

  彼得·福斯特

10 分钟阅读

考虑一下恶意行为者试图通过 API 注入、抓取、收获或窃取数据的情况。此类恶意活动通常以攻击者向 API 端点发起请求的特定顺序为特征。此外，单独使用容量技术通常不容易检测到恶意活动，因为攻击者可能会故意缓慢地执行 API 请求，以试图阻止容量滥用保护。因此，为了可靠地防止此类恶意活动，我们需要考虑 API 请求的顺序。我们使用术语“连续滥用”来指代恶意 API 请求行为。因此，我们的基本目标包括区分恶意 API 请求序列和良性 API 请求序列。

在这篇博文中，您将了解我们如何应对帮助客户保护其 API 免遭连续滥用的挑战。为此，我们将揭开目前支撑我们的序列分析产品的统计机器学习 (ML) 技术。我们将以之前的博客文章 中提供的序列分析高级介绍为基础。

API 会话

在上一篇博客文章中介绍过，让我们考虑一下由特定用户发起的一系列按时间排序的 HTTP API 请求的想法。这些发生在用户与服务交互时，例如在浏览网站或使用移动应用程序时。我们将用户按时间顺序排列的一系列 API 请求称为 会话。选择一个熟悉的示例，客户与银行服务交互的会话可能如下所示：

时间顺序

方法

小路

描述

1

邮政

/api/v1/auth

验证用户身份

2

得到

/api/v1/accounts/{帐户_id}

显示账户余额，其中account_id是属于该用户的账户

3

邮政

/api/v1/transferFunds

包含请求正文，详细说明资金转出帐户、资金转入帐户以及转帐金额

我们的目标之一是通过自动建议适用于我们的[序列]的规则，使我们的客户能够保护他们的 API缓解](https://developers.cloudflare.com/api-shield/security/sequence-mitigation/) 产品，用于强制执行所需的顺序行为。如果我们强制执行预期的行为，我们就可以防止不需要的顺序行为。在我们的示例中，所需的顺序行为可能需要 /api/v1/auth 必须始终位于 /api/v1/accounts/{account_id} 之前。

我们必须解决的一个重要挑战是可能的会话数量随着会话长度的增加而迅速增长。为了了解原因，我们可以考虑用户与示例银行服务交互的替代方式：例如，用户可以以任何顺序执行多次转账和/或检查多个帐户的余额。假设有 3 个可能的 端点，下图说明了用户与银行服务交互时可能出现的会话：

由于存在大量可能的会话，建议缓解规则要求我们解决从过去的会话数据中总结顺序行为作为中间步骤的挑战。在我们的示例中，我们将会话中的一系列连续端点（例如 /api/v1/accounts/{account_id} → /api/v1/transferFunds）称为 序列。具体来说，我们需要解决的一个挑战是，与创建规则相关的顺序行为并不一定仅从数量上显而易见：例如，考虑 /api/transferFunds 几乎总是在 /api/v1/accounts/{account\ _id}，而且与序列 /api/v1/auth → /api/v1/accounts/ 相比，序列 /api/v1/accounts/{account_id} → /api/v1/transferFunds 可能相对很少出现{帐户_id}。因此可以想象，如果我们仅根据交易量进行总结，我们可能会认为序列 /api/v1/accounts/{account_id} → /api/v1/transferFunds 不重要，而事实上我们应该浮出水面它作为一个潜在的规则。 

从 API 会话中学习重要序列

适用于顺序数据的广泛应用的建模方法是马尔可夫链，其中会话数据中每个端点的概率仅取决于固定数量的先前端点。首先，我们将展示如何将标准马尔可夫链应用于我们的会话数据，同时指出它们的一些局限性。其次，我们将展示如何使用不太知名但功能强大的马尔可夫链类型来确定重要序列。

出于说明目的，我们假设会话数据中有 3 个可能的端点。我们将使用字母 a、b 和 c 表示这些端点：

• a: /api/v1/auth

• b: /api/v1/accounts/{account_id}

• c: /api/v1/transferFunds

在最简单的形式中，马尔可夫链只不过是一个表格，它告诉我们在已知前一个字母的情况下下一个字母的概率。如果我们使用最简单的马尔可夫链对过去的会话数据进行建模，我们最终可能会得到一个像这样的表：

会话中已知的前一个端点

会话中下一个端点的估计概率

一个

乙

c

一个

0.10 (1555)

0.89 (13718)

0.01 (169)

乙

0.03 (9618)

0.63 (205084)

0.35 (113382)

c

0.02 (3340)

0.67 (109896)

0.31 (51553)

表1

表 1 列出了马尔可夫链的参数，即在已知会话中紧邻的前一个端点的情况下，观察 a、b 或 c 作为会话中下一个端点的估计概率。例如，值为 0.67 的第 3 行单元格意味着已知紧邻的前一个端点 c，将 b 观察为会话中下一个端点的估计概率为 67%，无论 c 之前是否有任何端点。因此，表中的每个条目对应于两个端点的序列。括号中的值是我们在过去的会话数据中看到每个两个端点序列的次数，用于计算表中的概率。例如，值 0.01 是计算小数 169 / (1555+13718+169) 的结果。这种估计概率的方法称为“最大似然估计”(https://en.wikipedia.org/wiki/Maximum\_likelihood\_estimation)。

为了确定重要的序列，我们依靠可信区间来估计概率而不是最大似然估计。可信区间不是产生单点估计（如上所述），而是代表合理的概率范围。该范围反映了可用数据量，即每行中序列出现的总数。数据越多，可信区间越窄（确定性程度越高），相反，数据越少，可信区间越宽（确定性程度越低）。 根据上表中括号内的值，我们可以得到以下可信区间（粗体部分将在后面进一步解释）：

会话中已知的前一个端点

会话中下一个端点的估计概率

一个

乙

c

一个

0.09-0.11 (1555)

0.88-0.89 (13718)

0.01-0.01 (169)

乙

0.03-0.03 (9618)

0.62-0.63 (205084)

0.34-0.35 (113382)

c

0.02-0.02 (3340)

0.66-0.67 (109896)

0.31-0.32 (51553)

表2

为了简洁起见，我们不会在这里演示如何手动计算出可信区间（它们涉及评估 beta 分布 的分位数函数 ://en.wikipedia.org/wiki/Beta_distribution））。尽管如此，修订后的表表明更多数据如何导致可信区间缩小：请注意第一行总共出现 15442 次，而第二行总共出现 328084 次。

为了确定重要的序列，我们使用比上述那些稍微复杂的马尔可夫链。作为中间步骤，我们首先考虑每个表条目对应于 3 个端点（而不是上面的 2 个）的序列的情况，如下表所示：

会话中已知的先前端点

会话中下一个端点的估计概率

一个

乙

c

啊

0.09-0.13 (173)

0.86-0.90 (1367)

0.00-0.02 (13)

巴

0.09-0.11 (940)

0.88-0.90 (8552)

0.01-0.01 (109)

加州

0.09-0.12 (357)

0.87-0.90 (2945)

0.01-0.02 (35)

ab

0.02-0.02 (272)

0.56-0.58 (7823)

0.40-0.42 (5604)

BB

0.03-0.03 (6067)

0.60-0.60 (122796)

0.37-0.37 (75801)

CB

0.03-0.03 (3279)

0.68-0.68 (74449)

0.29-0.29 (31960)

交流电

0.01-0.09 (6)

0.77-0.91 (144)

0.06-0.19 (19)

公元前

0.02-0.02 (2326)

0.77-0.77 (87215)

0.21-0.21 (23612)

抄送

0.02-0.02 (1008)

0.43-0.44 (22527)

0.54-0.55 (27919)

表3

表 3 再次列出了观察 a、b 或 c 作为会话中下一个端点的估计概率，但前提是知道会话中 2 个紧邻前面的端点（而不是像以前那样紧邻 1 个前面的端点）。也就是说，间隔为 0.09-0.13 的第 3 行单元格意味着，在已知之前的端点 ca 的情况下，观察到 a 作为下一个端点的概率具有跨越 9% 和 13% 的可信区间，无论 * ca* 之前有任何端点。换句话说，我们说上表代表阶 2 的马尔可夫链。这是因为表中的条目代表观察下一个端点的概率，假设已知 2 个紧邻的前一个端点作为上下文 。

作为一种特殊情况，0 阶马尔可夫链仅表示会话中端点上的分布。我们可以将与“空上下文”对应的单行相关的概率制成如下表格：

会话中已知的先前端点

会话中下一个端点的估计概率

一个

乙

c

0.03-0.03 (15466)

0.64-0.65 (328732)

0.32-0.33 (165117)

表4

请注意，表 4 中的概率不仅仅代表会话中没有先前端点的情况。相反，概率是会话中端点出现的概率，对于我们不知道前面的端点并且无论先前出现了多少个端点的一般情况。    

回到我们识别重要序列的任务，一种可能的方法可能是简单地使用某个固定阶 N 的马尔可夫链。例如，如果我们将 0.85 的阈值应用于表 3 中可信区间的下限，那么我们总共会保留 3 个序列。另一方面，这种方法有两个值得注意的限制：

1. 我们需要一种方法来为模型阶数N选择合适的值。 

2. 由于模型阶数保持固定，因此识别出的序列都具有相同的长度N+1。

变阶马尔可夫链

变阶马尔可夫链（VOMC）是所描述的固定阶马尔可夫链的更强大的扩展，它解决了上述限制。 VOMC 利用这样一个事实，即对于固定阶 N 的马尔可夫链的某些选定值，概率表可能包含统计冗余信息：让我们比较上面的表 3 和表 2，并考虑表 3 中与上下文相对应的粗体行aa、ba、ca（这 3 个上下文都共享 _a_ 作为后缀）。

对于所有 3 个可能的下一个端点 a、b、c，这些行指定了可信区间，这些区间与表 2 中对应于上下文 a 的各自估计值重叠（也以粗体表示）。考虑到 a 作为前面的端点，我们可以将这些重叠间隔解释为表示概率估计之间没有明显差异。由于 a 之前的内容对下一个端点的概率没有明显影响，我们可以认为表 3 中的这 3 行是多余的：我们可以通过将它们替换为表 2 中与上下文 a 对应的行来“折叠”它们。

按所述修改表 3 的结果如下所示（新行以粗体表示）：

会话中已知的先前端点

会话中下一个端点的估计概率

一个

乙

c

一个

0.09-0.11 (1555)

0.88-0.89 (13718)

0.01-0.01 (169)

ab

0.02-0.02 (272)

0.56-0.58 (7823)

0.40-0.42 (5604)

交流电

0.03-0.03 (6067)

0.60-0.60 (122796)

0.37-0.37 (75801)

BB

0.03-0.03 (3279)

0.68-0.68 (74449)

0.29-0.29 (31960)

公元前

0.01-0.09 (6)

0.77-0.91 (144)

0.06-0.19 (19)

CB

0.02-0.02 (2326)

0.77-0.77 (87215)

0.21-0.21 (23612)

抄送

0.02-0.02 (1008)

0.43-0.44 (22527)

0.54-0.55 (27919)

表5

表 5 表示 VOMC，因为上下文长度有所不同：在示例中，我们有上下文长度 1 和 2。因此，表中的条目表示长度在 2 到 3 个端点之间变化的序列，具体取决于上下文长度。概括所描述的折叠上下文方法可得出以下用于在离线环境中学习 VOMC 的算法草图：

(1) 定义包含会话中下一个端点的估计概率的表，或者给出会话中的前一个端点“0, 1, 2, …, N_max”。也就是说，通过连接固定阶马尔可夫链‘0, 1, 2, …, N_max`` 对应的行形成一个表。

(2) is_modified := true 

(3) DO WHILE is_modified

(4) _D_ :=T 中的所有上下文，这些上下文不是T` 中至少 1 个其他上下文的后缀

(5) is_modified = false

(6) FOR _ctx_ IN _C_

(7) IF 长度(``_ctx_``) > 0

(8) _parent_ctx_ :=删除``_ctx_中最左边端点得到的上下文

(9) IF is_collapsible(``_ctx_``, _parent_ctx_``)

(10) 修改 _T_ 通过丢弃 _ctx_

(11) is_modified = true

在伪代码中，length(ctx) 是上下文ctx 的长度。在第 9 行，is_collapsible() 涉及以生成表 5 所描述的方式比较上下文 ctx 和 parent_ctx 的可信区间：is_collapsible() 计算结果为 true，当且仅当我们观察到当分别比较每个可能的下一个端点的上下文 ctx 和 parent_ctx 时，所有可信区间重叠。最大序列长度为 N_max+1_,_ 其中 N_max 是某个常数。在第 4 行，如果我们可以通过在 q 前面添加零个或多个端点来形成 p，则我们说上下文 q 是另一个上下文 p 的 后缀。 （根据这个定义，上面提到的 0 阶模型的“空上下文”是 T 中所有上下文的后缀。）上面的算法草图是 Rissanen 首先提出的想法的变体 [1]，Ron 等人。 [2]。

最后，我们将结果表 T 中的条目作为我们的重要序列。因此，应用 VOMC 的结果是一组我们认为重要的序列。然而，对于序列分析，我们认为对序列进行排名也很有用。我们通过计算 0.0 到 1.0 之间的“优先分数”来实现这一点，即序列出现的次数除以序列中最后一个端点出现的次数。因此，接近 1.0 的优先级分数表明给定端点几乎总是位于序列中的其余端点之前。通过这种方式，手动检查得分最高的序列是一种半自动启发式方法，用于在我们的序列缓解产品中创建优先规则。

大规模学习序列

前面内容对我们在序列分析中使用的统计机器学习技术进行了非常高级的概述。在实践中，我们设计了一种高效的算法，它不需要预先的训练步骤，而是在数据到达时不断更新模型，并生成重要序列的频繁更新的摘要。这种方法使我们能够克服本博文中未涉及的内存成本方面的其他挑战。最重要的是，上面算法草图的直接实现仍然会导致表行（上下文）的数量随着最大序列长度的增加而爆炸。我们必须解决的另一个挑战是如何确保我们的系统能够处理大量 API，而不会对 CPU 负载产生不利影响。我们预先使用水平可扩展的自适应采样策略，以便将更积极的采样应用于大容量 API。然后，我们的算法会使用 API 请求的采样流。客户加入后，序列会随着时间的推移进行组装和学习，因此重要序列的当前摘要代表一个回溯间隔约为 24 小时的滑动窗口。序列分析进一步将序列存储在 Clickhouse 中，并通过 GraphQL API 公开它们/) 并通过 Cloudflare 仪表板。希望强制执行序列规则的客户可以使用序列缓解 来执行此操作。序列缓解负责确保规则在 Cloudflare 全球网络上以分布式方式共享和匹配 - 未来博客文章的另一个令人兴奋的主题！

接下来是什么

现在您已经更好地了解了我们如何显示重要的 API 请求序列，请继续关注本系列的后续博文，我们将在其中描述如何找到客户可能想要阻止的异常 API 请求序列。目前，API Gateway 客户可以通过两种方式开始：使用序列分析 (Sequence Analytics)(https://developers.cloudflare.com/api-shield/security/sequence-analytics/) 来探索重要的 API 请求序列，以及使用序列分析 (Sequence Analytics) 来探索重要的 API 请求序列。缓解](https://developers.cloudflare.com/api-shield/security/sequence-mitigation/) 强制执行 API 请求序列。尚未购买 API Gateway 的企业客户可以通过在 Cloudflare 内启用 API Gateway 试用版 来开始使用仪表板或联系他们的客户经理。

Cloudflare 的连接云保护整个企业网络，帮助客户高效构建互联网规模的应用程序，加速任何网站或互联网应用程序、抵御 DDoS 攻击、 黑客陷入困境，并且可以帮助您完成[零信任之旅](https://www.cloudflare.com/products/zero-trust /）。

从任何设备访问 1.1.1.1，开始使用我们的免费应用程序，让您的互联网更快、更安全。

要详细了解我们帮助建立更好的互联网的使命，请从这里开始。如果您正在寻找新的职业方向，请查看我们的空缺职位。