diff --git a/Searching-Sorting Workshop/searching/1.md b/Searching-Sorting Workshop/searching/1.md
new file mode 100644
index 0000000..9097910
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/1.md
@@ -0,0 +1,12 @@
+** Type: ** Title slide
+
+** Title: ** Searching
+
+
+** Content** :
+
+*No content here just title for introduction*
+
+** Speaker's notes** :
+
+Briefly go about telling what this presentation will be about.
diff --git a/Searching-Sorting Workshop/searching/10.md b/Searching-Sorting Workshop/searching/10.md
new file mode 100644
index 0000000..c137f13
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/10.md
@@ -0,0 +1,36 @@
+** Type: ** Code steps
+
+** Title: ** Binary search implementation
+
+
+** Content** :
+```Python
+def binarySearch (arr, l, r, x):
+
+ # Check base case
+ if r >= l:
+
+ mid = l + (r - l)/2
+
+ # If element is present at the middle itself
+ if arr[mid] == x:
+ return mid
+
+ # If element is smaller than mid, then it
+ # can only be present in left subarray
+ elif arr[mid] > x:
+ return binarySearch(arr, l, mid-1, x)
+
+ # Else the element can only be present
+ # in right subarray
+ else:
+ return binarySearch(arr, mid + 1, r, x)
+
+ else:
+ # Element is not present in the array
+ return -1
+```
+
+
+** Speaker's notes** :
+Show the code in full and then break down the explanation part by part.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/searching/2.md b/Searching-Sorting Workshop/searching/2.md
new file mode 100644
index 0000000..1c48afb
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/2.md
@@ -0,0 +1,14 @@
+** Type: ** Headline
+
+** Title: ** Motivation to searching
+
+** Content** : Motivation to why we need searching
+
+add visual to help prove a point
+
+** Speaker's notes** :
+
+
+Suppose, for example, I love watching movies. I have collections of all of the *Harry Potter*, *The Lord of the Rings*, and *James Bond* films. I have invited some friends to binge-watch them with me tomorrow morning, but I woke up late and need to find the movies quickly! How can I find the movies that I want to watch in the most efficient manner possible, before the doorbell rings?
+
+Now extend this problem to wide-scale computer systems. What if we needed to find certain information (say, for example, medical records) from stored data in a timely fashion? What sort of algorithms should we implement? Luckily, Computer Scientists have developed answers for us!
diff --git a/Searching-Sorting Workshop/searching/3.md b/Searching-Sorting Workshop/searching/3.md
new file mode 100644
index 0000000..6764f52
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/3.md
@@ -0,0 +1,19 @@
+** Type: ** Text + Img
+
+** Title: ** Graphs
+
+
+** Content** :
+
+A graph in computer science is a visual representation of a set of nodes that are connected together by edges, and graphs allow us to view information and relationships in data structures.
+
+Add image of a graph
+
+
+
+** Speaker's notes** :
+
+
+What can we do with graphs? Graph traversal, or graph search, is the process of visiting each vertex in a graph. This is important because, as we traverse through a graph, we can change or update each vertex that is visited, which can be very useful!
+
+How can we store graphs? Graphs can be stored in lists and matrices, and for instance, the two most commonly-used methods to store a graph are in an adjacency list and an adjacency matrix. An adjacency list is an array that notes each node with the vertices that are directly connected, or adjacent, to it by an edge, and an adjacency matrix is a matrix that notes which nodes are adjacent to each other with a "1" (if the nodes are not adjacent, then this is noted by a "0").
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/searching/4.md b/Searching-Sorting Workshop/searching/4.md
new file mode 100644
index 0000000..bcf402a
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/4.md
@@ -0,0 +1,15 @@
+** Type: ** comparison left and right
+
+** Title: ** BFS & DFS
+
+
+** Content** :
+Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a 'search key'), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
+
+
+DFS - The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
+
+
+** Speaker's notes** :
+
+Highlight the two searching algorithm that you are going to discuss and their differences
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/searching/5.md b/Searching-Sorting Workshop/searching/5.md
new file mode 100644
index 0000000..c422443
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/5.md
@@ -0,0 +1,17 @@
+** Type: ** left image + text
+
+** Title: ** DFS
+
+
+** Content** :
+
+The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
+
+
+- **Rule 1** − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
+- **Rule 2** − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.)
+- **Rule 3** − Repeat Rule 1 and Rule 2 until the stack is empty.
+
+Add visual for help
+
+** Speaker's notes** :
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/searching/6.md b/Searching-Sorting Workshop/searching/6.md
new file mode 100644
index 0000000..2db5843
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/6.md
@@ -0,0 +1,27 @@
+** Type: ** Code steps
+
+** Title: ** DFS implementation
+
+
+** Content** :
+
+```python
+ def DFSUtil(self, v, visited):
+
+ #first breakdown
+ visited[v] = True
+ print(v, end = ' ')
+
+ #second breakdown
+ for i in self.graph[v]:
+ if visited[i] == False:
+ self.DFSUtil(i, visited)
+
+ #third breakdown
+ def DFS(self, v):
+ visited = [False] * (len(self.graph))
+ self.DFSUtil(v, visited)
+```
+
+** Speaker's notes** :
+Show the code in full and then break down the explanation part by part.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/searching/7.md b/Searching-Sorting Workshop/searching/7.md
new file mode 100644
index 0000000..307afe0
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/7.md
@@ -0,0 +1,14 @@
+** Type: ** left image + text
+
+** Title: ** BFS
+
+- **Rule 1** − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
+- **Rule 2** − If no adjacent vertex is found, remove the first vertex from the queue.
+- **Rule 3** − Repeat Rule 1 and Rule 2 until the queue is empty.
+
+Add visuals for explanation
+
+** Content** :
+
+** Speaker's notes** :
+Give indepth explanation of BFS without code
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/searching/8.md b/Searching-Sorting Workshop/searching/8.md
new file mode 100644
index 0000000..3278ec2
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/8.md
@@ -0,0 +1,30 @@
+** Type: ** Code steps
+
+** Title: ** BFS implementation
+
+
+** Content** :
+
+```python
+def BFS(self, s):
+ #1st breakdown
+ visited = [False] * (len(self.graph))
+ #2nd breakdown
+ queue = []
+ #3rd breakdown
+ queue.append(s)
+ visited[s] = True
+ #4th breakdown
+ while queue:
+ s = queue.pop(0)
+ print (s, end = " ")
+ #5th breakdown
+ for i in self.graph[s]:
+ if visited[i] == False:
+ queue.append(i)
+ visited[i] = True
+```
+
+
+** Speaker's notes** :
+Show the code in full and then break down the explanation part by part.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/searching/9.md b/Searching-Sorting Workshop/searching/9.md
new file mode 100644
index 0000000..5003e7a
--- /dev/null
+++ b/Searching-Sorting Workshop/searching/9.md
@@ -0,0 +1,13 @@
+** Type: ** left image + text
+
+** Title: ** Binary search
+
+
+** Content** :
+
+*Best explained with visuals*
+Just use visuals here and let the presenter explain binary search, many wordings in the slidies may cause confusion.
+
+** Speaker's notes** :
+
+Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/1.md b/Searching-Sorting Workshop/sorting/1.md
new file mode 100644
index 0000000..b97a862
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/1.md
@@ -0,0 +1,12 @@
+** Type: ** Title slide
+
+** Title: ** Sorting
+
+
+** Content** :
+
+*No content here just title for introduction*
+
+** Speaker's notes** :
+
+Briefly go about telling what this presentation will be about.
diff --git a/Searching-Sorting Workshop/sorting/10.md b/Searching-Sorting Workshop/sorting/10.md
new file mode 100644
index 0000000..8c5a0a2
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/10.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Insertion sort
+
+
+** Content** :
+Add this GIF
+
+for visualisation
+
+
+
+** Speaker's notes** :
+
+
+Insertion sort uproots the current element of a list, compares it to all previous elements that we have already looked it, and places it in the appropriate spot. Because of this, insertion sort only needs one pass to fully sort a list.
diff --git a/Searching-Sorting Workshop/sorting/11.md b/Searching-Sorting Workshop/sorting/11.md
new file mode 100644
index 0000000..0c9c6aa
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/11.md
@@ -0,0 +1,13 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 1
+
+
+** Content** :
+
+ +
+
+** Speaker's notes** :
+
+1. We first take the second element and compare it to the first. If it is smaller, we place it before the first element. We are trying to sort the array from smallest to largest. After this initial step, our sample list will look like this:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/12.md b/Searching-Sorting Workshop/sorting/12.md
new file mode 100644
index 0000000..12bb2e7
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/12.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 2
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+1. We first take the second element and compare it to the first. If it is smaller, we place it before the first element. We are trying to sort the array from smallest to largest. After this initial step, our sample list will look like this:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/12.md b/Searching-Sorting Workshop/sorting/12.md
new file mode 100644
index 0000000..12bb2e7
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/12.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 2
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+
+2. Move onto the next element, in this case 3. Since this is the third element, we compare it to the previous *two* elements. 3 is smaller than both 5 and 6, so it will be placed in the first position of our list. Our list now looks like this:
diff --git a/Searching-Sorting Workshop/sorting/13.md b/Searching-Sorting Workshop/sorting/13.md
new file mode 100644
index 0000000..d3a8e9a
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/13.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 1
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+2. Move onto the next element, in this case 3. Since this is the third element, we compare it to the previous *two* elements. 3 is smaller than both 5 and 6, so it will be placed in the first position of our list. Our list now looks like this:
diff --git a/Searching-Sorting Workshop/sorting/13.md b/Searching-Sorting Workshop/sorting/13.md
new file mode 100644
index 0000000..d3a8e9a
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/13.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 1
+
+
+** Content** :
+
+  +
+
+** Speaker's notes** :
+
+
+
+3. We continue down the list and keep repeating this process, comparing the nth element with the n - 1 previous elements, and adjusting its position until we get a fully sorted array as shown below:
+
+
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/14.md b/Searching-Sorting Workshop/sorting/14.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/14.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/15.md b/Searching-Sorting Workshop/sorting/15.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/15.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/16.md b/Searching-Sorting Workshop/sorting/16.md
new file mode 100644
index 0000000..8a51c93
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/16.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Merge sort
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+
+If we pretend we have to sort a deck of cards, Mergesort can be thought of as dividing up the work by cutting the deck into smaller, more manageable groups and rearranging the cards before bringing it all back together.
+
diff --git a/Searching-Sorting Workshop/sorting/17.md b/Searching-Sorting Workshop/sorting/17.md
new file mode 100644
index 0000000..b744a99
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/17.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 1
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+
+
+3. We continue down the list and keep repeating this process, comparing the nth element with the n - 1 previous elements, and adjusting its position until we get a fully sorted array as shown below:
+
+
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/14.md b/Searching-Sorting Workshop/sorting/14.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/14.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/15.md b/Searching-Sorting Workshop/sorting/15.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/15.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/16.md b/Searching-Sorting Workshop/sorting/16.md
new file mode 100644
index 0000000..8a51c93
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/16.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Merge sort
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+
+If we pretend we have to sort a deck of cards, Mergesort can be thought of as dividing up the work by cutting the deck into smaller, more manageable groups and rearranging the cards before bringing it all back together.
+
diff --git a/Searching-Sorting Workshop/sorting/17.md b/Searching-Sorting Workshop/sorting/17.md
new file mode 100644
index 0000000..b744a99
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/17.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 1
+
+
+** Content** :
+
+ +
+
+
+  +
+** Speaker's notes** :
+1. First, divide the list in half, or something close to it. It's alright if one half is bigger. This is just because there was an odd number of elements in our list. After this first division, our sample list now looks like this:
+
diff --git a/Searching-Sorting Workshop/sorting/18.md b/Searching-Sorting Workshop/sorting/18.md
new file mode 100644
index 0000000..a37fd5d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/18.md
@@ -0,0 +1,11 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 2
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+1. First, divide the list in half, or something close to it. It's alright if one half is bigger. This is just because there was an odd number of elements in our list. After this first division, our sample list now looks like this:
+
diff --git a/Searching-Sorting Workshop/sorting/18.md b/Searching-Sorting Workshop/sorting/18.md
new file mode 100644
index 0000000..a37fd5d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/18.md
@@ -0,0 +1,11 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 2
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+2. Keep dividing up each list in half until every original element is by itself:
diff --git a/Searching-Sorting Workshop/sorting/19.md b/Searching-Sorting Workshop/sorting/19.md
new file mode 100644
index 0000000..c1e3d7e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/19.md
@@ -0,0 +1,14 @@
+
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 3
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+2. Keep dividing up each list in half until every original element is by itself:
diff --git a/Searching-Sorting Workshop/sorting/19.md b/Searching-Sorting Workshop/sorting/19.md
new file mode 100644
index 0000000..c1e3d7e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/19.md
@@ -0,0 +1,14 @@
+
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 3
+
+
+** Content** :
+
+
+  +
+** Speaker's notes** :
+
+Now, try and pair elements together in order. Here, we are trying to sort from smallest to largest. In our sample list, the `7` will have to be by itself:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/2.md b/Searching-Sorting Workshop/sorting/2.md
new file mode 100644
index 0000000..7300f33
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/2.md
@@ -0,0 +1,15 @@
+** Type: ** Headline
+
+** Title: ** Motivation to sorting
+
+** Content** : Motivation to why we need sorting
+
+add visual to help prove a point
+
+** Speaker's notes** :
+
+When a program takes in data, a lot of times we need to have the data be in some kind of order before being able to use it. Think of the last time you bought something online. You probably used different criteria to search for something whether that was by price, rating, size, or some other category.
+
+Behind the scenes a program is putting each object in order depending on your desired criteria. This is where sorting comes in. When humans manually categorize something such as a deck of cards, each person may choose to do so in a different style. Some may search for the aces, then the twos and so on or some may sort them by suit first. While there is no wrong way to arrive at a sorted sequence, there is a difference in efficiency between methods.
+
+
diff --git a/Searching-Sorting Workshop/sorting/20.md b/Searching-Sorting Workshop/sorting/20.md
new file mode 100644
index 0000000..761aa9f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/20.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 4
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+Now, try and pair elements together in order. Here, we are trying to sort from smallest to largest. In our sample list, the `7` will have to be by itself:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/2.md b/Searching-Sorting Workshop/sorting/2.md
new file mode 100644
index 0000000..7300f33
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/2.md
@@ -0,0 +1,15 @@
+** Type: ** Headline
+
+** Title: ** Motivation to sorting
+
+** Content** : Motivation to why we need sorting
+
+add visual to help prove a point
+
+** Speaker's notes** :
+
+When a program takes in data, a lot of times we need to have the data be in some kind of order before being able to use it. Think of the last time you bought something online. You probably used different criteria to search for something whether that was by price, rating, size, or some other category.
+
+Behind the scenes a program is putting each object in order depending on your desired criteria. This is where sorting comes in. When humans manually categorize something such as a deck of cards, each person may choose to do so in a different style. Some may search for the aces, then the twos and so on or some may sort them by suit first. While there is no wrong way to arrive at a sorted sequence, there is a difference in efficiency between methods.
+
+
diff --git a/Searching-Sorting Workshop/sorting/20.md b/Searching-Sorting Workshop/sorting/20.md
new file mode 100644
index 0000000..761aa9f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/20.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 4
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+
+ Now we move on to pairing groups of elements. We make sure to sort all the elements first before combining them. After this step, our sample list will first look like this:
diff --git a/Searching-Sorting Workshop/sorting/21.md b/Searching-Sorting Workshop/sorting/21.md
new file mode 100644
index 0000000..e0a61f6
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/21.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 5
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+ Now we move on to pairing groups of elements. We make sure to sort all the elements first before combining them. After this step, our sample list will first look like this:
diff --git a/Searching-Sorting Workshop/sorting/21.md b/Searching-Sorting Workshop/sorting/21.md
new file mode 100644
index 0000000..e0a61f6
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/21.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 5
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+
+Now, we simply do one more sort-and-combine step to get our fully sorted list:
diff --git a/Searching-Sorting Workshop/sorting/22.md b/Searching-Sorting Workshop/sorting/22.md
new file mode 100644
index 0000000..76dde3b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/22.md
@@ -0,0 +1,48 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Merge
+sort implementation
+
+** Content** :
+
+
+```python
+def mergeSort(alist):
+ if len(alist) > 1:
+ mid = len(alist) // 2 # integer division
+ lefthalf = alist[:mid]
+ righthalf = alist[mid:]
+ mergeSort(lefthalf)
+ mergeSort(righthalf)
+
+ i = 0
+ j = 0
+ k = 0
+ while i < len(lefthalf) and j < len(righthalf):
+ if lefthalf[i] <= righthalf[j]:
+ alist[k]=lefthalf[i]
+ i=i+1
+ else:
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+
+ while i < len(lefthalf):
+ alist[k]=lefthalf[i]
+ i=i+1
+ k=k+1
+
+ while j < len(righthalf):
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+ ```
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/23.md b/Searching-Sorting Workshop/sorting/23.md
new file mode 100644
index 0000000..a6dd9eb
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/23.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 1
+
+
+** Content** :
+
+for visualisation
+
+
+
+** Speaker's notes** :
+
+Now, we simply do one more sort-and-combine step to get our fully sorted list:
diff --git a/Searching-Sorting Workshop/sorting/22.md b/Searching-Sorting Workshop/sorting/22.md
new file mode 100644
index 0000000..76dde3b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/22.md
@@ -0,0 +1,48 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Merge
+sort implementation
+
+** Content** :
+
+
+```python
+def mergeSort(alist):
+ if len(alist) > 1:
+ mid = len(alist) // 2 # integer division
+ lefthalf = alist[:mid]
+ righthalf = alist[mid:]
+ mergeSort(lefthalf)
+ mergeSort(righthalf)
+
+ i = 0
+ j = 0
+ k = 0
+ while i < len(lefthalf) and j < len(righthalf):
+ if lefthalf[i] <= righthalf[j]:
+ alist[k]=lefthalf[i]
+ i=i+1
+ else:
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+
+ while i < len(lefthalf):
+ alist[k]=lefthalf[i]
+ i=i+1
+ k=k+1
+
+ while j < len(righthalf):
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+ ```
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/23.md b/Searching-Sorting Workshop/sorting/23.md
new file mode 100644
index 0000000..a6dd9eb
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/23.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 1
+
+
+** Content** :
+
+for visualisation
+
+  +
+
+** Speaker's notes** :
+1. We first choose an element to be our "pivot point". There are many different strategies on how to pick the pivot point. For our example, we will choose a random element, `3` as our pivot. The code below chooses to always pick the last element in a list as the pivot.
+
diff --git a/Searching-Sorting Workshop/sorting/24.md b/Searching-Sorting Workshop/sorting/24.md
new file mode 100644
index 0000000..072c382
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/24.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 2
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+1. We first choose an element to be our "pivot point". There are many different strategies on how to pick the pivot point. For our example, we will choose a random element, `3` as our pivot. The code below chooses to always pick the last element in a list as the pivot.
+
diff --git a/Searching-Sorting Workshop/sorting/24.md b/Searching-Sorting Workshop/sorting/24.md
new file mode 100644
index 0000000..072c382
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/24.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 2
+
+
+** Content** :
+
+for visualisation
+
+  +
+** Speaker's notes** :
+
+Start at the left of the list and continue through until you come across a value higher than that of the pivot. In our case, we didn't need to move. The first element `6` is already larger than our pivot.
diff --git a/Searching-Sorting Workshop/sorting/25.md b/Searching-Sorting Workshop/sorting/25.md
new file mode 100644
index 0000000..80d913e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/25.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 3
+
+
+** Content** :
+
+for visualisation
+
+
+
+** Speaker's notes** :
+
+Start at the left of the list and continue through until you come across a value higher than that of the pivot. In our case, we didn't need to move. The first element `6` is already larger than our pivot.
diff --git a/Searching-Sorting Workshop/sorting/25.md b/Searching-Sorting Workshop/sorting/25.md
new file mode 100644
index 0000000..80d913e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/25.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 3
+
+
+** Content** :
+
+for visualisation
+
+  +
+
+
+  +
+** Speaker's notes** :
+Do the same starting from the right end of the list. Move left until you come across a value smaller than that the pivot. That would be the `2` in our example, the second-to-last element in the list.
+Swap these two values.
diff --git a/Searching-Sorting Workshop/sorting/26.md b/Searching-Sorting Workshop/sorting/26.md
new file mode 100644
index 0000000..982abe5
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/26.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 4
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+Do the same starting from the right end of the list. Move left until you come across a value smaller than that the pivot. That would be the `2` in our example, the second-to-last element in the list.
+Swap these two values.
diff --git a/Searching-Sorting Workshop/sorting/26.md b/Searching-Sorting Workshop/sorting/26.md
new file mode 100644
index 0000000..982abe5
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/26.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 4
+
+
+** Content** :
+
+for visualisation
+
+
+  +
+** Speaker's notes** :
+
+Continue moving in through the list, repeating steps 2-4 until both sides meet the pivot point. At this point, our list should look like this
diff --git a/Searching-Sorting Workshop/sorting/27.md b/Searching-Sorting Workshop/sorting/27.md
new file mode 100644
index 0000000..f4ee94d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/27.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 5
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+
+Continue moving in through the list, repeating steps 2-4 until both sides meet the pivot point. At this point, our list should look like this
diff --git a/Searching-Sorting Workshop/sorting/27.md b/Searching-Sorting Workshop/sorting/27.md
new file mode 100644
index 0000000..f4ee94d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/27.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 5
+
+
+** Content** :
+
+for visualisation
+
+
+  +
+
+** Speaker's notes** :
+
+We're done with `3`. Now we select a different pivot and repeat the process all over again. We keep doing this until we get a fully sorted list, as shown below:
diff --git a/Searching-Sorting Workshop/sorting/28.md b/Searching-Sorting Workshop/sorting/28.md
new file mode 100644
index 0000000..1d82668
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/28.md
@@ -0,0 +1,33 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Quicksort implementation
+
+** Content** :
+
+```python
+def partition(arr,low,high):
+ i = low - 1
+ pivot = arr[high]
+ for j in range(low, high):
+ if arr[j] < pivot:
+ i = i+1
+ arr[i],arr[j] = arr[j],arr[i]
+ arr[i+1],arr[high] = arr[high],arr[i+1]
+ return i+1
+
+def quickSort(arr,low,high):
+ if low < high:
+ pi = partition(arr,low,high)
+
+ quickSort(arr, low, pi-1)
+ quickSort(arr, pi+1, high)
+
+```
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/3.md b/Searching-Sorting Workshop/sorting/3.md
new file mode 100644
index 0000000..b8f5080
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/3.md
@@ -0,0 +1,14 @@
+** Type: ** Main point
+
+** Title: ** Types of sorting
+
+** Content** :
+
+- Bubble sort
+- Mergesort
+- Insertion Sort
+- Quicksort
+
+** Speaker's notes** :
+
+Briefly go over the sorts we are going to discuss
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/4.md b/Searching-Sorting Workshop/sorting/4.md
new file mode 100644
index 0000000..2a6e02d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/4.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Bubble sort
+
+
+** Content** :
+Add this GIF
+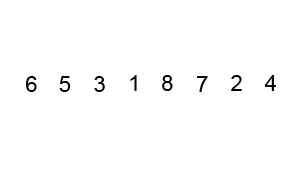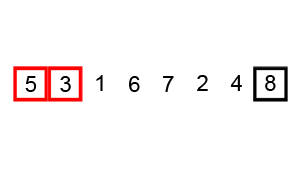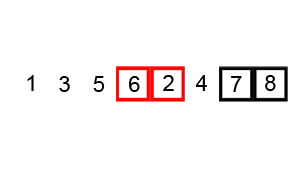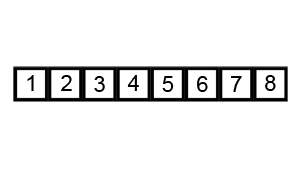
+for visualisation
+
+
+** Speaker's notes** :
+
+Bubble Sort is considered to be one of the simplest sorting algorithms. The name comes from the fact that this method compares two adjacent elements and swaps them if they're not in order. This makes larger values "bubble to the top" (to the very end of the list), giving us a fully sorted list in the end.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/5.md b/Searching-Sorting Workshop/sorting/5.md
new file mode 100644
index 0000000..01e2acf
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/5.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 1
+
+
+** Content** :
+
+
+
+
+
+** Speaker's notes** :
+
+We're done with `3`. Now we select a different pivot and repeat the process all over again. We keep doing this until we get a fully sorted list, as shown below:
diff --git a/Searching-Sorting Workshop/sorting/28.md b/Searching-Sorting Workshop/sorting/28.md
new file mode 100644
index 0000000..1d82668
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/28.md
@@ -0,0 +1,33 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Quicksort implementation
+
+** Content** :
+
+```python
+def partition(arr,low,high):
+ i = low - 1
+ pivot = arr[high]
+ for j in range(low, high):
+ if arr[j] < pivot:
+ i = i+1
+ arr[i],arr[j] = arr[j],arr[i]
+ arr[i+1],arr[high] = arr[high],arr[i+1]
+ return i+1
+
+def quickSort(arr,low,high):
+ if low < high:
+ pi = partition(arr,low,high)
+
+ quickSort(arr, low, pi-1)
+ quickSort(arr, pi+1, high)
+
+```
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/3.md b/Searching-Sorting Workshop/sorting/3.md
new file mode 100644
index 0000000..b8f5080
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/3.md
@@ -0,0 +1,14 @@
+** Type: ** Main point
+
+** Title: ** Types of sorting
+
+** Content** :
+
+- Bubble sort
+- Mergesort
+- Insertion Sort
+- Quicksort
+
+** Speaker's notes** :
+
+Briefly go over the sorts we are going to discuss
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/4.md b/Searching-Sorting Workshop/sorting/4.md
new file mode 100644
index 0000000..2a6e02d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/4.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Bubble sort
+
+
+** Content** :
+Add this GIF
+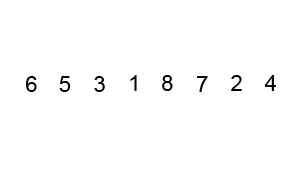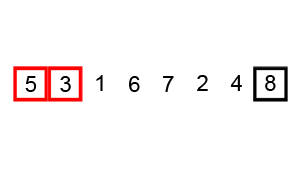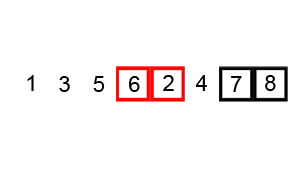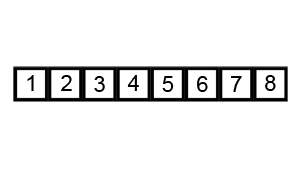
+for visualisation
+
+
+** Speaker's notes** :
+
+Bubble Sort is considered to be one of the simplest sorting algorithms. The name comes from the fact that this method compares two adjacent elements and swaps them if they're not in order. This makes larger values "bubble to the top" (to the very end of the list), giving us a fully sorted list in the end.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/5.md b/Searching-Sorting Workshop/sorting/5.md
new file mode 100644
index 0000000..01e2acf
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/5.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 1
+
+
+** Content** :
+
+
+ +
+** Speaker's notes** :
+
+
+1. Compare the first two numbers, if they are not sorted (the larger number comes before the smaller number), then swap the two. This assumes that you want the list elements to be sorted from smallest to largest. In our list, 6 comes before 5, so we swap the two.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/6.md b/Searching-Sorting Workshop/sorting/6.md
new file mode 100644
index 0000000..f97e96b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/6.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 2
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+
+1. Compare the first two numbers, if they are not sorted (the larger number comes before the smaller number), then swap the two. This assumes that you want the list elements to be sorted from smallest to largest. In our list, 6 comes before 5, so we swap the two.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/6.md b/Searching-Sorting Workshop/sorting/6.md
new file mode 100644
index 0000000..f97e96b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/6.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 2
+
+
+** Content** :
+
+
+ +
+** Speaker's notes** :
+
+
+2. Move on from the first and compare the second and third values, swap if necessary. In our case, 6 now comes before 3 so we swap again:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/7.md b/Searching-Sorting Workshop/sorting/7.md
new file mode 100644
index 0000000..07ff22f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/7.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 3
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+
+2. Move on from the first and compare the second and third values, swap if necessary. In our case, 6 now comes before 3 so we swap again:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/7.md b/Searching-Sorting Workshop/sorting/7.md
new file mode 100644
index 0000000..07ff22f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/7.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 3
+
+
+** Content** :
+
+  +
+
+** Speaker's notes** :
+
+
+3. Continue down the list until reaching the last element. At this point the largest value has been sorted. In our example, 8 is the largest number. So at this point, 8 should now be at the very last position of the list:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/8.md b/Searching-Sorting Workshop/sorting/8.md
new file mode 100644
index 0000000..9de5103
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/8.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 4
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+
+3. Continue down the list until reaching the last element. At this point the largest value has been sorted. In our example, 8 is the largest number. So at this point, 8 should now be at the very last position of the list:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/8.md b/Searching-Sorting Workshop/sorting/8.md
new file mode 100644
index 0000000..9de5103
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/8.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 4
+
+
+** Content** :
+
+ +
+
+** Speaker's notes** :
+
+
+4. We finished the first pass of the list. Now, we start over again from the first number, 5 in our case, and repeat steps 1-3. This time, however, we continue down the list to the *second-to-last* element. This is because we can see that 8 is in the position it should be. It doesn't need to be swapped anymore. We then repeat the whole process until we arrive at the
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/9.md b/Searching-Sorting Workshop/sorting/9.md
new file mode 100644
index 0000000..a48d317
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/9.md
@@ -0,0 +1,25 @@
+** Type: ** Code steps
+
+** Title: ** Bubble sort implementation
+
+** Content** :
+
+
+
+```python
+def bubbleSort(bubble):
+ for n in range(len(bubble)-1,0,-1):
+ for i in range(n):
+ if bubble[i] > bubble[i+1]:
+ temp = bubble[i]
+ bubble[i] = bubble[i+1]
+ bubble[i+1] = temp
+
+bubble = [14,46,43,27,57,41,45,21,70]
+bubbleSort(bubble)
+print(bubble)
+```
+
+** Speaker notes ** :
+
+Break down into steps
\ No newline at end of file
+
+
+** Speaker's notes** :
+
+
+4. We finished the first pass of the list. Now, we start over again from the first number, 5 in our case, and repeat steps 1-3. This time, however, we continue down the list to the *second-to-last* element. This is because we can see that 8 is in the position it should be. It doesn't need to be swapped anymore. We then repeat the whole process until we arrive at the
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/9.md b/Searching-Sorting Workshop/sorting/9.md
new file mode 100644
index 0000000..a48d317
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/9.md
@@ -0,0 +1,25 @@
+** Type: ** Code steps
+
+** Title: ** Bubble sort implementation
+
+** Content** :
+
+
+
+```python
+def bubbleSort(bubble):
+ for n in range(len(bubble)-1,0,-1):
+ for i in range(n):
+ if bubble[i] > bubble[i+1]:
+ temp = bubble[i]
+ bubble[i] = bubble[i+1]
+ bubble[i+1] = temp
+
+bubble = [14,46,43,27,57,41,45,21,70]
+bubbleSort(bubble)
+print(bubble)
+```
+
+** Speaker notes ** :
+
+Break down into steps
\ No newline at end of file
 +
+
+** Speaker's notes** :
+
+1. We first take the second element and compare it to the first. If it is smaller, we place it before the first element. We are trying to sort the array from smallest to largest. After this initial step, our sample list will look like this:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/12.md b/Searching-Sorting Workshop/sorting/12.md
new file mode 100644
index 0000000..12bb2e7
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/12.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 2
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+1. We first take the second element and compare it to the first. If it is smaller, we place it before the first element. We are trying to sort the array from smallest to largest. After this initial step, our sample list will look like this:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/12.md b/Searching-Sorting Workshop/sorting/12.md
new file mode 100644
index 0000000..12bb2e7
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/12.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 2
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+
+2. Move onto the next element, in this case 3. Since this is the third element, we compare it to the previous *two* elements. 3 is smaller than both 5 and 6, so it will be placed in the first position of our list. Our list now looks like this:
diff --git a/Searching-Sorting Workshop/sorting/13.md b/Searching-Sorting Workshop/sorting/13.md
new file mode 100644
index 0000000..d3a8e9a
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/13.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 1
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+2. Move onto the next element, in this case 3. Since this is the third element, we compare it to the previous *two* elements. 3 is smaller than both 5 and 6, so it will be placed in the first position of our list. Our list now looks like this:
diff --git a/Searching-Sorting Workshop/sorting/13.md b/Searching-Sorting Workshop/sorting/13.md
new file mode 100644
index 0000000..d3a8e9a
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/13.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+** Title: ** Insertion sort step by step 1
+
+
+** Content** :
+
+  +
+
+** Speaker's notes** :
+
+
+
+3. We continue down the list and keep repeating this process, comparing the nth element with the n - 1 previous elements, and adjusting its position until we get a fully sorted array as shown below:
+
+
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/14.md b/Searching-Sorting Workshop/sorting/14.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/14.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/15.md b/Searching-Sorting Workshop/sorting/15.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/15.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/16.md b/Searching-Sorting Workshop/sorting/16.md
new file mode 100644
index 0000000..8a51c93
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/16.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Merge sort
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+
+If we pretend we have to sort a deck of cards, Mergesort can be thought of as dividing up the work by cutting the deck into smaller, more manageable groups and rearranging the cards before bringing it all back together.
+
diff --git a/Searching-Sorting Workshop/sorting/17.md b/Searching-Sorting Workshop/sorting/17.md
new file mode 100644
index 0000000..b744a99
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/17.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 1
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+
+
+3. We continue down the list and keep repeating this process, comparing the nth element with the n - 1 previous elements, and adjusting its position until we get a fully sorted array as shown below:
+
+
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/14.md b/Searching-Sorting Workshop/sorting/14.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/14.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/15.md b/Searching-Sorting Workshop/sorting/15.md
new file mode 100644
index 0000000..c5d9d30
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/15.md
@@ -0,0 +1,27 @@
+
+** Type: ** Code steps
+
+** Title: ** Insertion
+sort implementation
+
+** Content** :
+
+
+ ```python
+def insertionSort(arr):
+ for i in range(1, len(arr)):
+ key = arr[i]
+ j = i-1
+ while j >= 0 and key < arr[j]:
+ arr[j+1] = arr[j]
+ j -= 1
+ arr[j + 1] = key
+ ```
+
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/16.md b/Searching-Sorting Workshop/sorting/16.md
new file mode 100644
index 0000000..8a51c93
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/16.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Merge sort
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+
+If we pretend we have to sort a deck of cards, Mergesort can be thought of as dividing up the work by cutting the deck into smaller, more manageable groups and rearranging the cards before bringing it all back together.
+
diff --git a/Searching-Sorting Workshop/sorting/17.md b/Searching-Sorting Workshop/sorting/17.md
new file mode 100644
index 0000000..b744a99
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/17.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 1
+
+
+** Content** :
+
+ +
+
+
+  +
+** Speaker's notes** :
+1. First, divide the list in half, or something close to it. It's alright if one half is bigger. This is just because there was an odd number of elements in our list. After this first division, our sample list now looks like this:
+
diff --git a/Searching-Sorting Workshop/sorting/18.md b/Searching-Sorting Workshop/sorting/18.md
new file mode 100644
index 0000000..a37fd5d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/18.md
@@ -0,0 +1,11 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 2
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+1. First, divide the list in half, or something close to it. It's alright if one half is bigger. This is just because there was an odd number of elements in our list. After this first division, our sample list now looks like this:
+
diff --git a/Searching-Sorting Workshop/sorting/18.md b/Searching-Sorting Workshop/sorting/18.md
new file mode 100644
index 0000000..a37fd5d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/18.md
@@ -0,0 +1,11 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 2
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+2. Keep dividing up each list in half until every original element is by itself:
diff --git a/Searching-Sorting Workshop/sorting/19.md b/Searching-Sorting Workshop/sorting/19.md
new file mode 100644
index 0000000..c1e3d7e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/19.md
@@ -0,0 +1,14 @@
+
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 3
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+2. Keep dividing up each list in half until every original element is by itself:
diff --git a/Searching-Sorting Workshop/sorting/19.md b/Searching-Sorting Workshop/sorting/19.md
new file mode 100644
index 0000000..c1e3d7e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/19.md
@@ -0,0 +1,14 @@
+
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 3
+
+
+** Content** :
+
+
+  +
+** Speaker's notes** :
+
+Now, try and pair elements together in order. Here, we are trying to sort from smallest to largest. In our sample list, the `7` will have to be by itself:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/2.md b/Searching-Sorting Workshop/sorting/2.md
new file mode 100644
index 0000000..7300f33
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/2.md
@@ -0,0 +1,15 @@
+** Type: ** Headline
+
+** Title: ** Motivation to sorting
+
+** Content** : Motivation to why we need sorting
+
+add visual to help prove a point
+
+** Speaker's notes** :
+
+When a program takes in data, a lot of times we need to have the data be in some kind of order before being able to use it. Think of the last time you bought something online. You probably used different criteria to search for something whether that was by price, rating, size, or some other category.
+
+Behind the scenes a program is putting each object in order depending on your desired criteria. This is where sorting comes in. When humans manually categorize something such as a deck of cards, each person may choose to do so in a different style. Some may search for the aces, then the twos and so on or some may sort them by suit first. While there is no wrong way to arrive at a sorted sequence, there is a difference in efficiency between methods.
+
+
diff --git a/Searching-Sorting Workshop/sorting/20.md b/Searching-Sorting Workshop/sorting/20.md
new file mode 100644
index 0000000..761aa9f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/20.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 4
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+Now, try and pair elements together in order. Here, we are trying to sort from smallest to largest. In our sample list, the `7` will have to be by itself:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/2.md b/Searching-Sorting Workshop/sorting/2.md
new file mode 100644
index 0000000..7300f33
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/2.md
@@ -0,0 +1,15 @@
+** Type: ** Headline
+
+** Title: ** Motivation to sorting
+
+** Content** : Motivation to why we need sorting
+
+add visual to help prove a point
+
+** Speaker's notes** :
+
+When a program takes in data, a lot of times we need to have the data be in some kind of order before being able to use it. Think of the last time you bought something online. You probably used different criteria to search for something whether that was by price, rating, size, or some other category.
+
+Behind the scenes a program is putting each object in order depending on your desired criteria. This is where sorting comes in. When humans manually categorize something such as a deck of cards, each person may choose to do so in a different style. Some may search for the aces, then the twos and so on or some may sort them by suit first. While there is no wrong way to arrive at a sorted sequence, there is a difference in efficiency between methods.
+
+
diff --git a/Searching-Sorting Workshop/sorting/20.md b/Searching-Sorting Workshop/sorting/20.md
new file mode 100644
index 0000000..761aa9f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/20.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 4
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+
+ Now we move on to pairing groups of elements. We make sure to sort all the elements first before combining them. After this step, our sample list will first look like this:
diff --git a/Searching-Sorting Workshop/sorting/21.md b/Searching-Sorting Workshop/sorting/21.md
new file mode 100644
index 0000000..e0a61f6
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/21.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 5
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+ Now we move on to pairing groups of elements. We make sure to sort all the elements first before combining them. After this step, our sample list will first look like this:
diff --git a/Searching-Sorting Workshop/sorting/21.md b/Searching-Sorting Workshop/sorting/21.md
new file mode 100644
index 0000000..e0a61f6
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/21.md
@@ -0,0 +1,12 @@
+** Type: ** Center img outline
+
+** Title: ** Merge sort step by step 5
+
+
+** Content** :
+
+  +
+** Speaker's notes** :
+
+Now, we simply do one more sort-and-combine step to get our fully sorted list:
diff --git a/Searching-Sorting Workshop/sorting/22.md b/Searching-Sorting Workshop/sorting/22.md
new file mode 100644
index 0000000..76dde3b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/22.md
@@ -0,0 +1,48 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Merge
+sort implementation
+
+** Content** :
+
+
+```python
+def mergeSort(alist):
+ if len(alist) > 1:
+ mid = len(alist) // 2 # integer division
+ lefthalf = alist[:mid]
+ righthalf = alist[mid:]
+ mergeSort(lefthalf)
+ mergeSort(righthalf)
+
+ i = 0
+ j = 0
+ k = 0
+ while i < len(lefthalf) and j < len(righthalf):
+ if lefthalf[i] <= righthalf[j]:
+ alist[k]=lefthalf[i]
+ i=i+1
+ else:
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+
+ while i < len(lefthalf):
+ alist[k]=lefthalf[i]
+ i=i+1
+ k=k+1
+
+ while j < len(righthalf):
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+ ```
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/23.md b/Searching-Sorting Workshop/sorting/23.md
new file mode 100644
index 0000000..a6dd9eb
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/23.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 1
+
+
+** Content** :
+
+for visualisation
+
+
+
+** Speaker's notes** :
+
+Now, we simply do one more sort-and-combine step to get our fully sorted list:
diff --git a/Searching-Sorting Workshop/sorting/22.md b/Searching-Sorting Workshop/sorting/22.md
new file mode 100644
index 0000000..76dde3b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/22.md
@@ -0,0 +1,48 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Merge
+sort implementation
+
+** Content** :
+
+
+```python
+def mergeSort(alist):
+ if len(alist) > 1:
+ mid = len(alist) // 2 # integer division
+ lefthalf = alist[:mid]
+ righthalf = alist[mid:]
+ mergeSort(lefthalf)
+ mergeSort(righthalf)
+
+ i = 0
+ j = 0
+ k = 0
+ while i < len(lefthalf) and j < len(righthalf):
+ if lefthalf[i] <= righthalf[j]:
+ alist[k]=lefthalf[i]
+ i=i+1
+ else:
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+
+ while i < len(lefthalf):
+ alist[k]=lefthalf[i]
+ i=i+1
+ k=k+1
+
+ while j < len(righthalf):
+ alist[k]=righthalf[j]
+ j=j+1
+ k=k+1
+ ```
+
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/23.md b/Searching-Sorting Workshop/sorting/23.md
new file mode 100644
index 0000000..a6dd9eb
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/23.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 1
+
+
+** Content** :
+
+for visualisation
+
+  +
+
+** Speaker's notes** :
+1. We first choose an element to be our "pivot point". There are many different strategies on how to pick the pivot point. For our example, we will choose a random element, `3` as our pivot. The code below chooses to always pick the last element in a list as the pivot.
+
diff --git a/Searching-Sorting Workshop/sorting/24.md b/Searching-Sorting Workshop/sorting/24.md
new file mode 100644
index 0000000..072c382
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/24.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 2
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+1. We first choose an element to be our "pivot point". There are many different strategies on how to pick the pivot point. For our example, we will choose a random element, `3` as our pivot. The code below chooses to always pick the last element in a list as the pivot.
+
diff --git a/Searching-Sorting Workshop/sorting/24.md b/Searching-Sorting Workshop/sorting/24.md
new file mode 100644
index 0000000..072c382
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/24.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 2
+
+
+** Content** :
+
+for visualisation
+
+  +
+** Speaker's notes** :
+
+Start at the left of the list and continue through until you come across a value higher than that of the pivot. In our case, we didn't need to move. The first element `6` is already larger than our pivot.
diff --git a/Searching-Sorting Workshop/sorting/25.md b/Searching-Sorting Workshop/sorting/25.md
new file mode 100644
index 0000000..80d913e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/25.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 3
+
+
+** Content** :
+
+for visualisation
+
+
+
+** Speaker's notes** :
+
+Start at the left of the list and continue through until you come across a value higher than that of the pivot. In our case, we didn't need to move. The first element `6` is already larger than our pivot.
diff --git a/Searching-Sorting Workshop/sorting/25.md b/Searching-Sorting Workshop/sorting/25.md
new file mode 100644
index 0000000..80d913e
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/25.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 3
+
+
+** Content** :
+
+for visualisation
+
+  +
+
+
+  +
+** Speaker's notes** :
+Do the same starting from the right end of the list. Move left until you come across a value smaller than that the pivot. That would be the `2` in our example, the second-to-last element in the list.
+Swap these two values.
diff --git a/Searching-Sorting Workshop/sorting/26.md b/Searching-Sorting Workshop/sorting/26.md
new file mode 100644
index 0000000..982abe5
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/26.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 4
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+Do the same starting from the right end of the list. Move left until you come across a value smaller than that the pivot. That would be the `2` in our example, the second-to-last element in the list.
+Swap these two values.
diff --git a/Searching-Sorting Workshop/sorting/26.md b/Searching-Sorting Workshop/sorting/26.md
new file mode 100644
index 0000000..982abe5
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/26.md
@@ -0,0 +1,16 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 4
+
+
+** Content** :
+
+for visualisation
+
+
+  +
+** Speaker's notes** :
+
+Continue moving in through the list, repeating steps 2-4 until both sides meet the pivot point. At this point, our list should look like this
diff --git a/Searching-Sorting Workshop/sorting/27.md b/Searching-Sorting Workshop/sorting/27.md
new file mode 100644
index 0000000..f4ee94d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/27.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 5
+
+
+** Content** :
+
+for visualisation
+
+
+
+
+** Speaker's notes** :
+
+Continue moving in through the list, repeating steps 2-4 until both sides meet the pivot point. At this point, our list should look like this
diff --git a/Searching-Sorting Workshop/sorting/27.md b/Searching-Sorting Workshop/sorting/27.md
new file mode 100644
index 0000000..f4ee94d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/27.md
@@ -0,0 +1,17 @@
+** Type: ** Center img outline
+
+
+** Title: ** Quicksort step 5
+
+
+** Content** :
+
+for visualisation
+
+
+  +
+
+** Speaker's notes** :
+
+We're done with `3`. Now we select a different pivot and repeat the process all over again. We keep doing this until we get a fully sorted list, as shown below:
diff --git a/Searching-Sorting Workshop/sorting/28.md b/Searching-Sorting Workshop/sorting/28.md
new file mode 100644
index 0000000..1d82668
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/28.md
@@ -0,0 +1,33 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Quicksort implementation
+
+** Content** :
+
+```python
+def partition(arr,low,high):
+ i = low - 1
+ pivot = arr[high]
+ for j in range(low, high):
+ if arr[j] < pivot:
+ i = i+1
+ arr[i],arr[j] = arr[j],arr[i]
+ arr[i+1],arr[high] = arr[high],arr[i+1]
+ return i+1
+
+def quickSort(arr,low,high):
+ if low < high:
+ pi = partition(arr,low,high)
+
+ quickSort(arr, low, pi-1)
+ quickSort(arr, pi+1, high)
+
+```
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/3.md b/Searching-Sorting Workshop/sorting/3.md
new file mode 100644
index 0000000..b8f5080
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/3.md
@@ -0,0 +1,14 @@
+** Type: ** Main point
+
+** Title: ** Types of sorting
+
+** Content** :
+
+- Bubble sort
+- Mergesort
+- Insertion Sort
+- Quicksort
+
+** Speaker's notes** :
+
+Briefly go over the sorts we are going to discuss
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/4.md b/Searching-Sorting Workshop/sorting/4.md
new file mode 100644
index 0000000..2a6e02d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/4.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Bubble sort
+
+
+** Content** :
+Add this GIF
+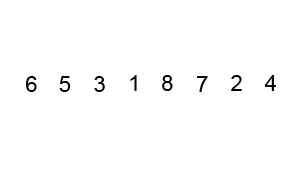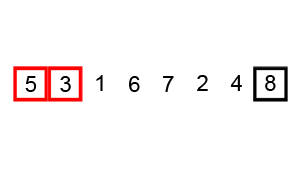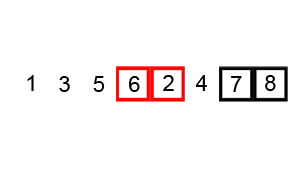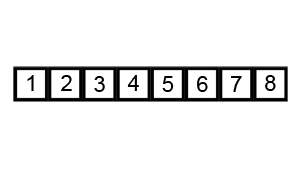
+for visualisation
+
+
+** Speaker's notes** :
+
+Bubble Sort is considered to be one of the simplest sorting algorithms. The name comes from the fact that this method compares two adjacent elements and swaps them if they're not in order. This makes larger values "bubble to the top" (to the very end of the list), giving us a fully sorted list in the end.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/5.md b/Searching-Sorting Workshop/sorting/5.md
new file mode 100644
index 0000000..01e2acf
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/5.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 1
+
+
+** Content** :
+
+
+
+
+
+** Speaker's notes** :
+
+We're done with `3`. Now we select a different pivot and repeat the process all over again. We keep doing this until we get a fully sorted list, as shown below:
diff --git a/Searching-Sorting Workshop/sorting/28.md b/Searching-Sorting Workshop/sorting/28.md
new file mode 100644
index 0000000..1d82668
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/28.md
@@ -0,0 +1,33 @@
+
+
+** Type: ** Code steps
+
+** Title: ** Quicksort implementation
+
+** Content** :
+
+```python
+def partition(arr,low,high):
+ i = low - 1
+ pivot = arr[high]
+ for j in range(low, high):
+ if arr[j] < pivot:
+ i = i+1
+ arr[i],arr[j] = arr[j],arr[i]
+ arr[i+1],arr[high] = arr[high],arr[i+1]
+ return i+1
+
+def quickSort(arr,low,high):
+ if low < high:
+ pi = partition(arr,low,high)
+
+ quickSort(arr, low, pi-1)
+ quickSort(arr, pi+1, high)
+
+```
+
+
+** Speaker notes ** :
+
+Break down into steps
+
diff --git a/Searching-Sorting Workshop/sorting/3.md b/Searching-Sorting Workshop/sorting/3.md
new file mode 100644
index 0000000..b8f5080
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/3.md
@@ -0,0 +1,14 @@
+** Type: ** Main point
+
+** Title: ** Types of sorting
+
+** Content** :
+
+- Bubble sort
+- Mergesort
+- Insertion Sort
+- Quicksort
+
+** Speaker's notes** :
+
+Briefly go over the sorts we are going to discuss
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/4.md b/Searching-Sorting Workshop/sorting/4.md
new file mode 100644
index 0000000..2a6e02d
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/4.md
@@ -0,0 +1,15 @@
+** Type: ** Center img outline
+
+
+** Title: ** Bubble sort
+
+
+** Content** :
+Add this GIF
+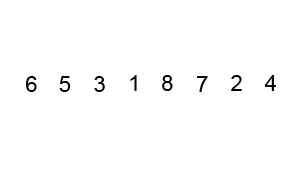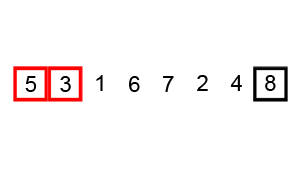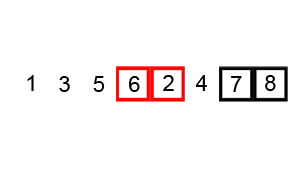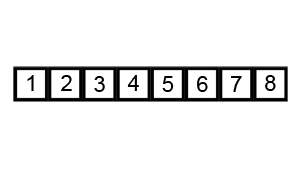
+for visualisation
+
+
+** Speaker's notes** :
+
+Bubble Sort is considered to be one of the simplest sorting algorithms. The name comes from the fact that this method compares two adjacent elements and swaps them if they're not in order. This makes larger values "bubble to the top" (to the very end of the list), giving us a fully sorted list in the end.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/5.md b/Searching-Sorting Workshop/sorting/5.md
new file mode 100644
index 0000000..01e2acf
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/5.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 1
+
+
+** Content** :
+
+
+ +
+** Speaker's notes** :
+
+
+1. Compare the first two numbers, if they are not sorted (the larger number comes before the smaller number), then swap the two. This assumes that you want the list elements to be sorted from smallest to largest. In our list, 6 comes before 5, so we swap the two.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/6.md b/Searching-Sorting Workshop/sorting/6.md
new file mode 100644
index 0000000..f97e96b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/6.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 2
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+
+1. Compare the first two numbers, if they are not sorted (the larger number comes before the smaller number), then swap the two. This assumes that you want the list elements to be sorted from smallest to largest. In our list, 6 comes before 5, so we swap the two.
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/6.md b/Searching-Sorting Workshop/sorting/6.md
new file mode 100644
index 0000000..f97e96b
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/6.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 2
+
+
+** Content** :
+
+
+ +
+** Speaker's notes** :
+
+
+2. Move on from the first and compare the second and third values, swap if necessary. In our case, 6 now comes before 3 so we swap again:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/7.md b/Searching-Sorting Workshop/sorting/7.md
new file mode 100644
index 0000000..07ff22f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/7.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 3
+
+
+** Content** :
+
+
+
+** Speaker's notes** :
+
+
+2. Move on from the first and compare the second and third values, swap if necessary. In our case, 6 now comes before 3 so we swap again:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/7.md b/Searching-Sorting Workshop/sorting/7.md
new file mode 100644
index 0000000..07ff22f
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/7.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 3
+
+
+** Content** :
+
+  +
+
+** Speaker's notes** :
+
+
+3. Continue down the list until reaching the last element. At this point the largest value has been sorted. In our example, 8 is the largest number. So at this point, 8 should now be at the very last position of the list:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/8.md b/Searching-Sorting Workshop/sorting/8.md
new file mode 100644
index 0000000..9de5103
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/8.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 4
+
+
+** Content** :
+
+
+
+
+** Speaker's notes** :
+
+
+3. Continue down the list until reaching the last element. At this point the largest value has been sorted. In our example, 8 is the largest number. So at this point, 8 should now be at the very last position of the list:
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/8.md b/Searching-Sorting Workshop/sorting/8.md
new file mode 100644
index 0000000..9de5103
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/8.md
@@ -0,0 +1,14 @@
+** Type: ** Center img outline
+
+** Title: ** Bubble sort step by step 4
+
+
+** Content** :
+
+ +
+
+** Speaker's notes** :
+
+
+4. We finished the first pass of the list. Now, we start over again from the first number, 5 in our case, and repeat steps 1-3. This time, however, we continue down the list to the *second-to-last* element. This is because we can see that 8 is in the position it should be. It doesn't need to be swapped anymore. We then repeat the whole process until we arrive at the
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/9.md b/Searching-Sorting Workshop/sorting/9.md
new file mode 100644
index 0000000..a48d317
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/9.md
@@ -0,0 +1,25 @@
+** Type: ** Code steps
+
+** Title: ** Bubble sort implementation
+
+** Content** :
+
+
+
+```python
+def bubbleSort(bubble):
+ for n in range(len(bubble)-1,0,-1):
+ for i in range(n):
+ if bubble[i] > bubble[i+1]:
+ temp = bubble[i]
+ bubble[i] = bubble[i+1]
+ bubble[i+1] = temp
+
+bubble = [14,46,43,27,57,41,45,21,70]
+bubbleSort(bubble)
+print(bubble)
+```
+
+** Speaker notes ** :
+
+Break down into steps
\ No newline at end of file
+
+
+** Speaker's notes** :
+
+
+4. We finished the first pass of the list. Now, we start over again from the first number, 5 in our case, and repeat steps 1-3. This time, however, we continue down the list to the *second-to-last* element. This is because we can see that 8 is in the position it should be. It doesn't need to be swapped anymore. We then repeat the whole process until we arrive at the
\ No newline at end of file
diff --git a/Searching-Sorting Workshop/sorting/9.md b/Searching-Sorting Workshop/sorting/9.md
new file mode 100644
index 0000000..a48d317
--- /dev/null
+++ b/Searching-Sorting Workshop/sorting/9.md
@@ -0,0 +1,25 @@
+** Type: ** Code steps
+
+** Title: ** Bubble sort implementation
+
+** Content** :
+
+
+
+```python
+def bubbleSort(bubble):
+ for n in range(len(bubble)-1,0,-1):
+ for i in range(n):
+ if bubble[i] > bubble[i+1]:
+ temp = bubble[i]
+ bubble[i] = bubble[i+1]
+ bubble[i+1] = temp
+
+bubble = [14,46,43,27,57,41,45,21,70]
+bubbleSort(bubble)
+print(bubble)
+```
+
+** Speaker notes ** :
+
+Break down into steps
\ No newline at end of file