Skip to content

Latest commit

 

History

History
221 lines (136 loc) · 17.5 KB

dfs.md

File metadata and controls

221 lines (136 loc) · 17.5 KB
Raw

Графы — определения, деревья, хранение и поиск в глубину

Основные определения

Формальное определение:

Графом $G$ называется пара множеств $G = (V, E$, где $V(G)$ — непустое конечное множество элементов, называемых вершинами графа, а $E$ — множество пар элементов из $V$ (необязательно различных), называемых ребрами графа. $E = {(u , v)\ | u, v \in V}$ — множество ребер графа $G$, состоящее из пар вершин $(u, v)$. Ребро $(u, v)$ соединяет вершины $u$ и $v$.

Простое определение:

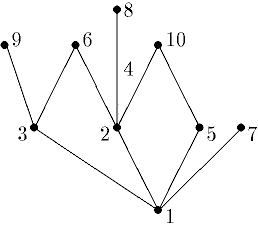
Граф - это набор вершин (точек) и соединяющих их отрезков (рёбер).

Примеры графа

Две вершины, соединенные ребром, называют смежными вершинами. Обычно в задачах $N$ - количество вершин, а $M$ - ребер. Количество ребер, исходящее из вершины называют степенью вершины $d(v)$. Для вершины $a$ ребро $(a, b)$ называется инцидентным ей. На рисунке ниже вершине 8 инцидентно только ребро (4, 8), а вершине 10 ребра (2, 10) и (5, 10).

Теоретическое задание

Назовите степень 1-ой и 6-ой вершины и какие ребра инциденты им.

1

Если какие-то две вершины соединены более, чем одним ребром, то говорят, что граф содержит кратные ребра. Если ребро соединяет вершину саму с собой, то такое ребро называют петлей.

Простой граф не содержит петель и кратных ребер. Если не сказано ничего про наличие петель и кратных ребер, мы будем всегда считать, что граф простой.

Теоретическое задание

Сколько может быть рёбер в простом графе в $N$ вершинами?

2

Теоретическое задание

Найдите цикл размера 4 и петлю в этом непростом графе.

Также часто рассматривают ориентированные графы — это графы, у которых ребра имеют направление, а иначе граф – неориентированный.

Хранение графа в программе

Чаще всего в задачах по программмированию вершины графа - это числа от $0$ до $N-1$, чтобы удобно было обращаться к ним как к индексам в разных массивах.

Также чаще всего вам дают считать граф как просто список всех рёбер в нем (но не всегда, конечно). Как оптимально считать и сохранить граф? Есть 3 способа.

Для графа существуют несколько основных способов хранения:

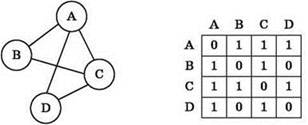
  1. Матрица смежности. Давайте хранить двумерную матрицу $A_{nn}$, где для данного графа G верно, что если $A_{ij}$ = 1, то две вершины $i$ и $j$ являются смежными, иначе вершины $i$ и $j$ смежными не являются.

Граф G и Матрица смежности

Мы храним для каждой из $N$ вершин информацию, есть ли ребро в другие вершины, то есть суммарно мы храним $N^2$ ячеек, а следовательно асимптотика по памяти - $O(N^2)$.

  1. Список смежности. Давайте для каждой из $N$ вершин хранить все смежные с ней, для этого нам потребуется любая динамическая структура, например vector в с++.
// как сделать список по матрице
vector<vector<int> > g(n);
for (int i = 0; i < n; ++i){
    for (int j = 0;j < n;++j){
        cin >> a;
        if (a) g[i].push_back(j);
    }
}
// список по списку ребер
cin >> n >> m;
vector<vector<int> > g(n);
for (int i = 0; i < m; ++i){
  cin >> v1 >> v2;
  g[v1].push_back(v2);
  g[v2].push_back(v1);
}

Здесь асимптотика по памяти и времени считывания - $O(N + M)$, так как мы храним для каждой вершины, куда есть ребра, то есть $2 M$ ребер, а также суммарно $N$ векторов.

Плотные графы, имеющие большое количество ребер следует хранить при помощи матрицы смежности, а разреженные графы, имеющие малое количество ребер, оптимальнее при помощи списка.

  1. Список рёбер. Иногда граф явно вообще не требуется, а хватает хранить просто список ребер, который нам дают на вход.

Заметьте, что все эти способы обощаются на случай ориентированных графов - при этом матрица смежности становится неориетированной: если есть ребро из вершины $i$ в вершину $j$, то сделаем $A_{ij} = 1$, а $A_{ji} = 0$, если только нет обратного ребра тоже. А в списке смежности в ориентированном случае при считывании ребра $(u, v)$ будем добавлять только $v$ в список соседей $u$, но не наоборот.

Практическое задание

Для окончательного закрепления темы советую решить первые 2 задачи.

Деревья

Дерево - это связный неориентированный граф без циклов.

Пример дерева

Свойства дерева:

  1. У дерева с хотя бы 2 вершинами всегда есть висячая вершина - вершина степени 1.

Действительно, если начать из любой вершины идти по непосещенным ранее вершинам, то в какой-то момент мы прекратим это делать, ведь граф конечный. При этом если из этой вершины не может быть ребер в непосещенные вершины - ведь тогда прекращать рано, и не может быть ребер в посещенные ребра (помимо предыдущей) - ведь тогда есть цикл. А значит, есть ребро только в предыдущую вершину, значит степень равна 1.

  1. У дерева с хотя бы 2 вершинами всегда есть две висячие вершины.

Действительно, если предыдущий алгоритм начать из висячей вершины, то мы уткнемся в другую висячую вершину.

  1. У дерева с $N$ вершинами всегда ровно $N-1$ ребро.

Давайте отрезать от дерева его висячие вершины - при этом число вершин уменьшится на один, число ребер тоже уменьшится на один, а граф останется деревом. Раз граф остается деревом, у него все время будет висячая вершина, пока $N &gt; 1$. В какой-то момент останется только одна вершина и ноль ребер. Раз мы отрезали столько же вершин, сколько ребер, и получили 1 вершину и 0 ребер, значит изначально вершин было ровно на одну больше.

  1. Между любыми двумя вершинами в дереве есть ровно один простой путь.

Действительно, если их два, то в графе есть цикл. Быть ноль их не может - ведь граф связный.

  1. Дерево - это минимальный по числу рёбер связный граф на $N$ вершинах.

Действительно, если есть связный граф, в котором меньше, чем $N-1$ ребро, то давайте уберем из его цикла ребро. Граф при этом остается связным, а число ребер уменьшается. Давайте повторять это, пока в какой-то момент циклов в графе не будет, а значит осталось дерево. Но мы уже доказали, что в дереве $N-1$ ребро, это противоречие, ведь у нас сначала было меньше ребер, а мы еще и удалили сколько-то.

DFS (Алгоритм обхода графа в глубину)

Обход в глубину — простой, но многофункциональный алгоритм обхода графа по ребрам. Самое главное, что он может — это проверить, какие вершины достижимы из данной.

При обходе графа мы используем вспомогательный массив used, в котором храним 1, если вершина была посещена или 0 иначе. В начале мы считаем, что все вершины не использовались, затем мы выбираем одну вершину, помечаем ее посещенной и запускаемся рекурсивно из всех ее соседей, тогда мы посетим все вершины, которые достижимы из данной, если же остались вершины с used = 0 значит они недостижимы.

Красивая визуализация: https://visualgo.net/en/dfsbfs

void dfs (int v) {
  used[v] = 1;
  for (auto to : g[v]) {
      if (!used[to]) {
          dfs(to);
      }
  }
}

Давайте оценим сложность алгоритма. Так как мы проверяем, что вершина еще не использовалась, то всего мы пройдет каждую вершину 1 раз, но при этом и ребро между двумя вершинами, мы рассматриваем только когда рассматривается один конец, то есть мы просмотрим каждое ребро не более одного раза, суммарно получаем оценку $O(N + M)$.

Практическое задание

Задачи 3-5 в контесте.

Поиск компонент связности графа

Путем в графе называется последовательность вершин $v_i \in 𝑉$, $i = 1...k$ таких, что две последовательные вершины в пути соединены ребром, $k$ - длина пути. Граф называется связным, если для любых двух его вершин существует путь между ними. Граф всегда можно разбить на непересекающиеся связные подмножества (возможно одно), между которыми рёбер нет, они называются компонентами связности.

Поиск в глубину dfs будет обходить ту компоненту связности, из вершины которой, он был вызван. Поэтому для поиска компонент связности можно каждый раз вызываться из любой непосещенной вершины и тогда в результате мы посетим все вершины, а следовательно и найдем все компоненты связности.

Граф с тремя компонентами связности

for (int i = 0; i < n; ++i){
    if (!used[i]) {
        amount++;
        dfs(i);
    }
}

Практическое задание

На данную тему задачи 6 и 10 в контесте.

Остовное дерево

Остованым деревом в связном графе называется любое подмножество ребер, которое является деревом на всех вершинах. То есть любой способ выкинуть несколько ребер так, чтобы осталось дерево на N вершинах и N-1 ребро выделяет в графе остовное дерево.

Обход графа удобно использовать для выделения этого остовного дерева - если выделить каждое ребро, по которому мы прошли в обходе, то получится остовное дерево. Действительно, мы обойдем все вершины, и при этом никогда не пойдем в вершину, в которой уже были, поэтому циклов там не будет. Так что достаточно после прохода по любому ребру добавлять его в ответ.

Практическое задание

7 задача в контесте на выделение остовного дерева в графе.

Раскраска графа в два цвета

Корректной раскраской графа в два цвета назывется такая раскраска, что никакое ребро не соединяет две вершины одного цвета. Графы, которые можно так раскрасить, называют еще двудольными.

С помощью обхода графа легко проверить граф на двудольность и даже вывести цвет каждой вершины - достаточно выделить каждую.

Практическое задание

8 задача в контесте на раскраску графа в два цвета

Поиск циклов в графе

Циклом в графе $G$ называется ненулевой путь, ведущий из вершины $v$ в саму себя. Граф называют ацикличным, если в нем нет циклов.

В обычном dfs мы используем два цвета (1 - вершина посещена, 0 - не посещена), если же нам надо найти цикл, то давайте хранить 3 цвета:

  • 0 - вершина не просмотрена
  • 1 - мы входили DFS-ом в эту вершину, но еще не вышли (а значит из нее есть путь до текущей),
  • 2 - мы входили DFS-ом в эту вершину

Заметим, что цикл будет тогда и только тогда, когда мы пытаемся войти в вершину с цветом 1.

void dfs (int v) {
    used[v] = 1;
    for (size_t i=0; i < g[v].size(); ++i) {
        int to = g[v][i];
        if (used[to] == 0){
            p[to] = v;
            dfs (to);
        }
        else if (used[to] == 1 && to != p[v]) {
            cycle = true;
        }
    }
    used[v] = 2;
}

В неориентированном графе также надо дополнительно рассмотреть случай, когда мы идем в предка - это циклом все-таки не считается, для этого нужно отдельно добавить второй аргумент prev, где хранить предыдущую вершину в dfs, и никогда не идти в неё.

Практическое задание

9 задача в контесте на поиск цикла в графе.

#Ссылка на контест

https://informatics.msk.ru/mod/statements/view3.php?id=33377