sparse-table.md

Разреженная таблица

Разреженная таблица (англ. sparse table) — структура данных, позволяющая отвечать на запросы минимума на отрезке за $O(1)$ с препроцессингом за $O(n \log n)$ времени и памяти.

Определение. Разреженная таблица — это следующий двумерный массив размера $\log n \times n$:

$$ t[k][i] = \min { a_i, a_{i+1}, \ldots, a_{i+2^k-1} } $$

По-русски: считаем минимумы на каждом отрезке длины $2^k$.

Такой массив можно посчитать за его размер, итерируясь либо по $i$, либо по $k$:

$$ t[k][i] = \min(t[k-1][i], t[k-1][i+2^{k-1}]) $$

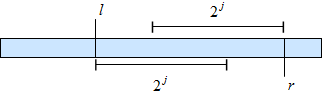
Имея таком массив, мы можем для любого отрезка быстро посчитать минимум на нём. Заметим, что у любого отрезка имеется два отрезка длины степени двойки, которые пересекаются, и, главное, покрывают его и только его целиком. Значит, мы можем просто взять минимум из значений, которые соответствуют этим отрезкам.

Последняя деталь: для того, чтобы константа на запрос стала настоящей, нужно научиться считать сам логарифм за константу. Для этого можно воспользоваться доступной в GCC функцией __lg. Она внутри использует инструкцию clz ("count leading zeros"), которая присутствует в большинстве современных процессоров и возвращает количество нулей до первой единицы в бинарной записи, из чего за несколько процессорных тактов можно получить нужный округленный логарифм.

int a[maxn], mn[logn][maxn];

int rmq(int l, int r) { // полуинтервал [l; r)
    int t = __lg(r - l);
    return min(mn[t][l], mn[t][r - (1 << t)]);
}

// Это считается где-то в первых строчках main:

memcpy(mn[0], a, sizeof a);

for (int l = 0; l < logn - 1; l++)
    for (int i = 0; i + (2 << l) <= n; i++)
        mn[l+1][i] = min(mn[l][i], mn[l][i + (1 << l)]);

Для больших таблиц порядок итерирования и расположение данных в памяти сильно влияет на скорость построения — это связано с работой кэшей. Но в большинстве случаев время построения не так критично.

Упражнение. Подумайте, в чём недостатки других 4 вариантов итерирования и layout-а.

Интересно, что последний цикл не векторизуется компилятором автоматически (видимо, потому что std::min это что-то сложное внутри), и поэтому замена тела цикла на конструкцию вида (x < y ? x : y) ускоряет построение ещё в ~2 раза.

Применения

Разреженная таблица является статической структурой данных, то есть её нельзя дёшево обновлять (но можно достраивать на ходу — см. задачу «Антиматерия» с РОИ-2017).

Разреженную таблицу часто применяют для решения задачи о наименьшем общем предке, так как её можно свести к RMQ.

2d Static RMQ

Эту структуру тоже можно обобщить на большие размерности. Пусть мы хотим посчитать RMQ на подквадратах. Тогда вместо массива t[k][i] у нас будет массив t[k][i][j], в котором вместо минимума на отрезах будет храниться минимум на квадратах тех же степеней двоек. Получение минимума на произвольном квадрате тогда уже распадется на четыре минимума на квадратах длины $2^k$.

В общем же случае от нас просят минимум на прямоугольниках $d$-мерного массива. Тогда делаем предподсчет, аналогичный предыдущему случаю, только теперь тут будет $O(n \log^d n)$ памяти и времени на предподсчет — нужно хранить минимумы на всех гипер-прямоугольниках со сторонами степени двойки.

Ограничения на операцию

Разреженную таблицу можно применять не только для минимума или максимума. От операции требуется только ассоциативность ($a ∘ (b ∘ c) = (a ∘ b) ∘ c$), коммутативность ($a ∘ b = b ∘ a$) и идемпотентность ($a ∘ a = a$). Например, её можно применять для нахождения $\gcd$.

Если операция не идемпотентна, то для нахождения её результата можно действовать так: возьмём самый длинный упирающийся в левую границу запроса отрезок, прибавим его к ответу, сдвинем указатель на его правый конец и будем так продолжать, пока не обработаем весь запрос целиком.

int sum(int l, int r) { // [l, r)
    int res = 0;
    for (int d = logn - 1; d >= 0; d--) {
        if (l + (1 << d) < r) {
            res += t[l][d];
            l += (1 << d);
        }
    }
    return res;
}

Это работает быстрее, чем, например, дерево отрезков, но тоже асимптотически за $O(\log n)$, да ещё и с дополнительной памятью. Но есть способ это ускорить.

Disjoint Sparse Table

Мы хотим иметь какую-то структуру, которая может считать функцию $f$ на отрезке, при том что $f$ не удовлетворяет условию идемпотентности. Стандартная разреженная таблица тут не подойдёт — в ней нельзя найти $O(1)$ непересекающихся отрезков.

Сделаем следующее: мысленно построим на массиве дерево отрезков и (уже не мысленно) для каждого его отрезка $[l, r)$ посчитаем $f$ на всех отрезках от его центрального элемента — то есть от элемента с индексом $m = \lfloor \frac{l + r}{2} \rfloor$ — до всех остальных элементов $k \in [l, r)$. Для каждого элемента массива будет $O(\log n)$ центральных, а значит суммарно на это потребуются те же $O(n \log n)$ времени и памяти.

Утверждение. Любой запрос $[l, r)$ разбивается на $O(1)$ непересекающихся предпосчитанных интервалов.

Доказательство. Возьмем самый высокий центральный элемент $m$, принадлежащий запросу. Его отрезок полностью покрыает запрос — если бы это было не так, то самым высоким был бы не $m$, а какая-то из его границ . Раз отрезок запроса $[l, r)$ полностью покрыт, и $m$ лежит внутри него, то $[l, r)$ можно разбить на предпосчитанные $[l, m)$ и $[m, r)$.

Решать задачу мы так и будем: найдём нужный центральный элемент и сделаем два запроса от него.

Реализация

Сложная часть — найти этот центральный элемент за константное время — станет чуть проще, если мы будем работать только с массивами длины степени двойки и, соответственно, полными деревьями отрезков. Массивы неподходящей длины дополним до ближайшей степени двойки специальным нейтральным элементом, зависящим от самой операции (например, $0$ для сложения или $1$ для умножения).

Будем хранить всю структуру (предпосчитанные значения на отрезках) в массиве t[logn][maxn], в котором первым параметром будет уровень в дереве отрезков (число $d$ для отрезков размера $2^d$), а вторым — граница соответствующего интервала (число $k$). Этой информации достаточно, чтобы однозначно восстановить отрезок.

Для ответа на запрос нам достаточно найти только уровень нужного центрального элемента. Чтобы научиться делать это эффективно, нам понадобится немного поразмышлять о природе дерева отрезков.

Заметим, что любая вершина $k$-того уровня соответствует какому-то отрезку $[l, l + 2^k)$, причём $l$ делится на $2^k$. Двоичное представление всех индексов на этом отрезке будет иметь какой-то общий префикс, а последние $k$ знаков будут различными.

Нам нужно найти уровень нужного центрального элемента — это то же самое, что и уровень наименьшего общего отрезка для элементов $l$ и $r$. Используя предыдущий факт, получаем, что искомый уровень будет равен позиции самого значимого бита, который отличается у чисел $l$ и $r$. Его можно найти за константное время выражением $h_{[l,r)]} = \lfloor \log_2 (l \oplus r) \rfloor$, если заранее предпосчитать логарифмы.

Для примера, построим DST для умножения по составному модулю:

const int maxn = (1 << logn);
int a[maxn], lg[maxn], t[logn][maxn];

const int neutral = 1;
int f(int a, int b) {
    return (a * b) % 1000;
}

void build(int l, int r, int level = logn - 1) {
    int m = (l + r) / 2;

    int cur = neutral;
    for (int i = m + 1; i < r; i++) {
        cur = f(cur, a[i]);
        t[level][i] = cur;
    }

    cur = neutral;
    for (int i = m; i >= l; i--) {
        cur = f(cur, a[i]);
        t[level][i] = cur;
    }

    if (r - l > 1) {
        build(l, mid, level+1);
        build(mid, r, level+1);
    }
}

int rmq(int l, int r) { // [l, r)
    int level = lg[l ^ r];
    int res = t[level][l];
    // и, если правый отрезок не пустой:
    if (r & ((1 << lg[l ^ r]) - 1)))
        res = f(res, t[level][r]);
    return res;
}

TODO: очень вероятно, тут есть баги.