Рассмотрим такую распространённую операцию как умножение двух целых чисел. Квадратичный алгоритм — умножения в столбик — все знают со школы. Долгое время предполагалось, что ничего быстрее придумать нельзя.
Первым эту гипотезу опроверг Анатолий Карацуба. Его алгоритм сводит умножение двух
Чтобы перейти к алгоритму с лучшей оценкой, нам нужно сначала установить несколько фактов о многочленах.
Обратим внимание на то, что любое число можно представить многочленом:
Основание x при этом может быть выбрано произвольно.
Чтобы перемножить два числа, мы можем перемножить соответствующие им многочлены, а затем произвести каррирование: пройтись от нижних разрядов получившегося многочлена и «сдвинуть» переполнившиеся разряды:
const int base = 10;
vector<int> normalize(vector<int> a) {
int carry = 0;
for (int &x : a) {
x += carry;
carry = x / base;
x %= base;
}
while (carry > 0) {
a.push_back(carry % base);
carry /= base;
}
return a;
}
vector<int> multiply(vector<int> a, vector<int> b) {
return normalize(poly_multiply(a, b));
}Прямая формула для произведения многочленов имеет вид
Её подсчёт требует
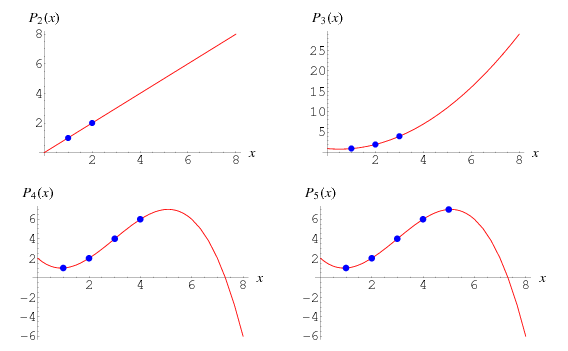
Теорема. Пусть есть набор различных точек
Доказательство будет конструктивным — можно явным образом задать многочлен, который принимает заданные значения
Корректность. Проверим, что в точке
-
Для
$i$ -го слагаемого внутреннее произведение будет равно единице, если вместо$x$ подставить$x_i$ : в этом случае просто перемножается$(n-1)$ единица. Эта единица помножится на$y_i$ и войдёт в сумму. -
Для всех остальных слагаемых произведение занулится: один из множетелей будет равен
$(x_i - x_i)$ .
Уникальность. Предположим, есть два подходящих многочлена степени
для какого-то числа
Этот многочлен называется интерполяционным многочленом Лагранжа, а сама задача проведения многочлена через точки — интерполяцией.
Примечание. На практике интерполяцию решают методом Гаусса: её можно свести к решению линейного уравнения
Важный факт: многочлен можно однозначно задать не только своими коэффициентами, но также корнями и значениями хотя бы в
Что происходит со значениями многочлена-произведения
Основная идея алгоритма: если мы знаем значения в каких-то различных
vector<int> poly_multiply(vector<int> a, vector<int> b) {
vector<int> A = evaluate(a);
vector<int> B = evaluate(b);
for (int i = 0; i < A.size(); i++)
A[i] *= B[i];
return interpolate(A);
}Если притвориться, что evaluate и interpolate работают за линейное время, то умножение тоже будет работать за линейное время.
К сожалению, непосредственное вычисление значений требует
Но что, если бы мы могли вычислять значения в точках и делать интерполяцию быстрее?
Определение. Комплексные числа — это числа вида
Комплексные числа ввели в алгебре, чтобы работать с корнями из отрицательных чисел:
С комплексными числами можно работать почти так же, как с действительными. Они даже удобнее: все квадратные корни всегда извлекаются, все корни многочленов всегда находятся.
Комплексные числа удобно изображать на плоскости в виде вектора
Модулем комплексного числа называется действительное число
Аргументом комплексного числа называется действительное число
Таким образом комплексное число можно представить в полярных координатах:
Подобное представление удобно по следующей причине: чтобы перемножить два комплексных числа, нужно перемножить их модули и сложить аргументы.
Упражнение. Докажите это.
Определим число Эйлера
Просто введём такую нотацию для выражения
Геометрически, все такие точки живут на единичном круге:
Такая нотация удобна, потому что можно обращаться с
Упражнение. Проверьте это: раскройте скобки и проделайте немного алгебры.
У комплексных чисел есть много других замечательных свойств, но нам для алгоритма на самом деле потребуется только следующее:
Утверждение. Для любого натурального
А именно, это будут числа вида:
где
На комплексной плоскости эти числа располагаются на единичном круге на равном расстоянии друг от друга:
Первый корень
Будем обозначать
Упражнение. Докажите, что других корней быть не может.
Дискретным преобразованием Фурье называется вычисление значений многочлена в комплексных корнях из единицы:
Обратным дискретным преобразованием Фурье называется, как можно догадаться, обратная операция — интерполяция коэффициентов
Почему эта формула верна? При вычислении ПФ мы практически применяем матрицу к вектору:
То есть преобразование Фурье — это просто линейная операция над вектором:
Как будет выглядеть эта
Проверим, что при перемножении
-
Значение
$i$ -того диагонального элемента будет равно$\frac{1}{n} \sum_k w^{ki} w^{-ki} = \frac{1}{n} n = 1$ . -
Значение любого недиагонального (
$i \neq j$ ) элемента$(i, j)$ будет равно$\frac{1}{n} \sum_k w^{ik} w^{-jk} = \frac{1}{n} \sum_k w^k w^{i-j} = \frac{w^{i-j}}{n} \sum_k w^k = 0$ , потому что все комплексные корни суммируются в ноль, то есть$\sum w^k = 0$ (см. картинку — там всё симметрично).
Внимательный читатель заметит симметричность форм
Напомним, что мы изначально хотели перемножать многочлены следующим алгоритмом:
-
Посчитаем значения в
$n+m$ каких-нибудь точках обоих многочленов -
Перемножим эти значения за
$O(n+m)$ . -
Интерполяцией получим многочлен-произведение.
В общем случае быстро посчитать интерполяцию и даже просто посчитать значения в точках нельзя, но для корней единицы — можно. Если научиться быстро считать значения в корнях и интерполировать (прямое и обратное преобразование Фурье), но мы можно решить исходную задачу.
Соответствующий алгоритм называется быстрым преобразованием Фурье (англ. fast Fourier transform). Он использует парадигму «разделяй-и-властвуй» и работает за
Обычно, алгоритмы «разделяй-и-властвуй» делят задачу на две половины: на первые
Представим многочлен в виде
Пусть
Зная это, исходную формулу для значения многочлена в точке
Ключевое замечание: корней вида
У нас по сути в два раза меньше корней (но они так же равномерно распределены на единичной окружности) и в два раза меньше коэффициентов — мы только что успешно уменьшили нашу задачу в два раз.
Сам алгоритм заключается в следующем: рекурсивно посчитаем БПФ для многочленов
Заметим, что если
Таким образом, мы свели преобразование размера
Заметим, что предположение о делимости
Приведём код, вычисляющий БПФ по схеме Кули-Тьюки:
typedef complex<double> ftype;
const double pi = acos(-1);
template<typename T>
vector<ftype> fft(vector<T> p, ftype w) {
int n = p.size();
if(n == 1)else { {
return {p[0]};
else {
vector<T> AB[2];
for(int i = 0; i < n; i++)
AB[i % 2].push_back(p[i]);
auto A = fft(AB[0], w * w);
auto B = fft(AB[1], w * w);
vector<ftype> res(n);
ftype wt = 1;
int k = n / 2;
for(int i = 0; i < n; i++) {
res[i] = A[i % k] + wt * B[i % k];
wt *= w;
}
return res;
}
}
vector<ftype> evaluate(vector<int> p) {
while(__builtin_popcount(p.size()) != 1)
p.push_back(0);
return fft(p, polar(1., 2 * pi / p.size()));
}Как обсуждалось выше, обратное преобразование Фурье удобно выразить через прямое:
vector<int> interpolate(vector<ftype> p) {
int n = p.size();
auto inv = fft(p, polar(1., -2 * pi / n));
vector<int> res(n);
for(int i = 0; i < n; i++)
res[i] = round(real(inv[i]) / n);
return res;
}Теперь мы умеем перемножать два многочлена за
vector<int> poly_multiply(vector<int> a, vector<int> b) {
vector<int> A = fft(a);
vector<int> B = fft(b);
for (int i = 0; i < A.size(); i++)
A[i] *= B[i];
return interpolate(A);
}Примечание. Приведённый выше код, являясь корректным и имея асимптотику
Читателю рекомендуется самостоятельно задуматься о том, как можно улучшить время работы и точность вычислений. Из наиболее важных недостатков:
-
внутри преобразования не должно происходить выделений памяти
-
работать желательно с указателями, а не векторами
-
корни из единицы должны быть посчитаны наперёд
-
Следует избавиться от операций взятия остатка по модулю
-
Вместо вычисления преобразования с
$w^{-1}$ можно вычислить преобразование с$w$ , а затем развернуть элементы массива со второго по последний.
Здесь приведена одна из условно пригодных реализаций.
Но главная проблема в численной стабильности — мы нарушили первое правило действительных чисел. Однако, от неё можно избавиться.
Нам от комплексных чисел на самом деле нужно было только одно свойство: что у единицы есть
Нам нужно просто найти такую пару
Это число простое, и при этом является ровно на единицу больше числа, делящегося на большую степень двойки. При
Реализация практически не отличается.
const int MOD = 998244353, W = 805775211, IW = 46809892;
const int MAXN = (1 << 19), INV2 = 499122177;
// W - первообразный корень MAXN-ной степени из 1, IW - обратное по модулю MOD к W
// Первообразный корень (1 << 23)-й степени из 1 по модулю MOD равен 31; тогда первообразный корень (1 << X)-й степени для X от 1 до 23 равен (31 * (1 << (23 - X))) % MOD
// INV2 - обратное к двум по модулю MOD
// Данная реализация FFT перемножает два целых числа длиной до 250000 цифр за ~0.13 секунд без проблем с точностью и занимает всего 30 строк кода
int pws[MAXN + 1], ipws[MAXN + 1];
void init() {
pws[MAXN] = W; ipws[MAXN] = IW;
for (int i = MAXN / 2; i >= 1; i /= 2) {
pws[i] = (pws[i * 2] * 1ll * pws[i * 2]) % MOD;
ipws[i] = (ipws[i * 2] * 1ll * ipws[i * 2]) % MOD;
}
}
void fft(vector<int> &a, vector<int> &ans, int l, int cl, int step, int n, bool inv) {
if (n == 1) { ans[l] = a[cl]; return; }
fft(a, ans, l, cl, step * 2, n / 2, inv);
fft(a, ans, l + n / 2, cl + step, step * 2, n / 2, inv);
int cw = 1, gw = (inv ? ipws[n] : pws[n]);
for (int i = l; i < l + n / 2; i++) {
int u = ans[i], v = (cw * 1ll * ans[i + n / 2]) % MOD;
ans[i] = (u + v) % MOD;
ans[i + n / 2] = (u - v) % MOD;
if (ans[i + n / 2] < 0) ans[i + n / 2] += MOD;
if (inv) {
ans[i] = (ans[i] * 1ll * INV2) % MOD;
ans[i + n / 2] = (ans[i + n / 2] * 1ll * INV2) % MOD;
}
cw = (cw * 1ll * gw) % MOD;
}
}С недавнего времени некоторые проблемсеттеры начали использовать именно этот модулю вместо стандартного
Даны две бинарные строки
$a$ и$b$ . Нужно найти такой циклический сдвиг строки$b$ , что количество совпадающих соответствующих символов с$a$ станет максимально.
Сперва научимся для каждого циклического сдвига