read401-15.md

Trees

Common Terminology

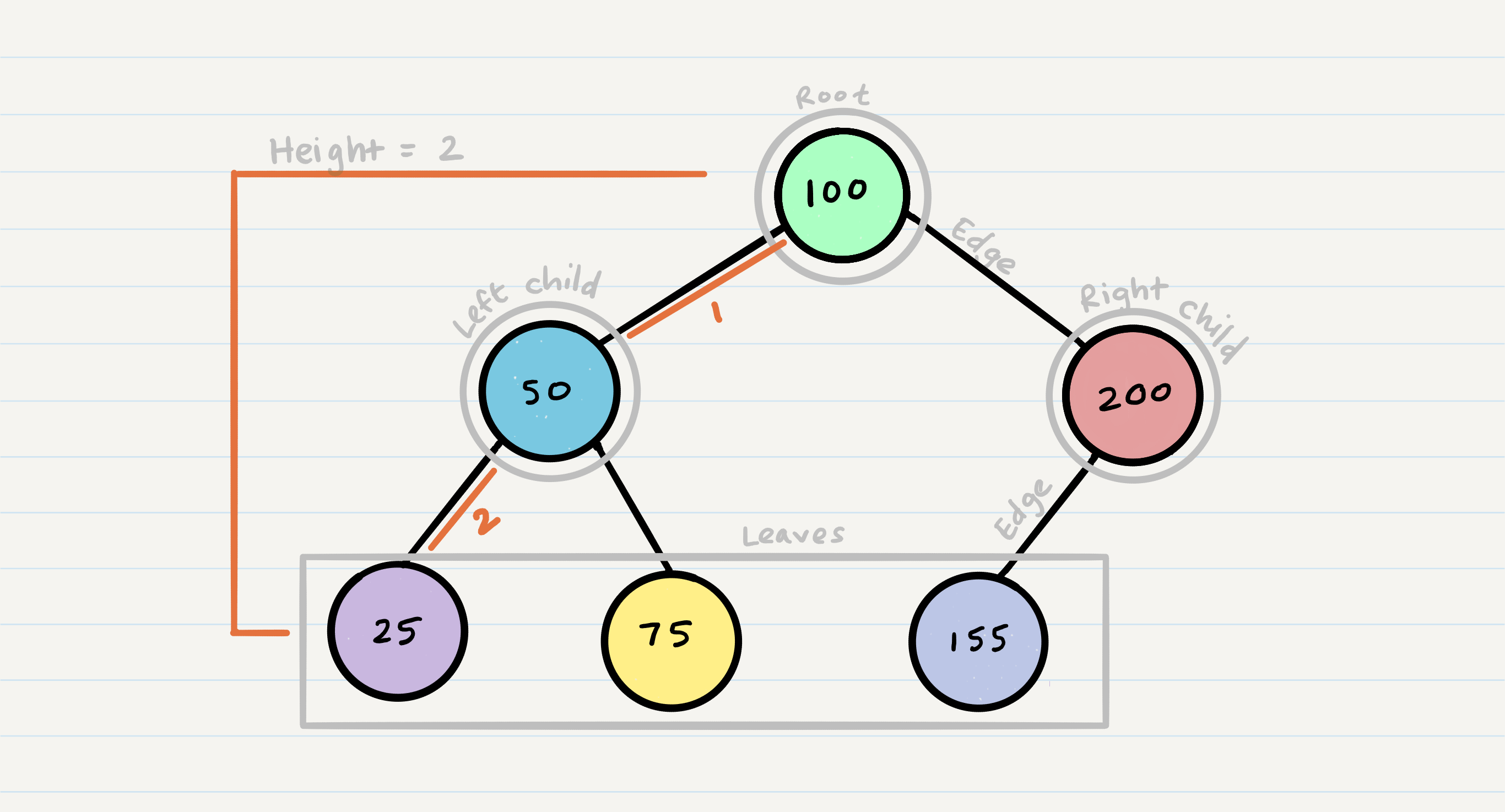
1. Node : a tree is combination of nodes that contain values
2. Root: the first node in tree
3. K : the number of children
4. Left : A reference to one child node, in a binary tree
5. Right : A reference to the other child node, in a binary tree
6. Edge : The edge in a tree is the link between a parent and child node
7. Leaf : A leaf is a node that does not have any children
8. Height : The height of a tree is the number of edges from the root to the furthest lea

Depth First

The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking

Pre-order: root >> left >> right

ALGORITHM preOrder(root)
// INPUT <-- root node
// OUTPUT <-- pre-order output of tree node's values

    OUTPUT <-- root.value

    if root.left is not Null
        preOrder(root.left)

    if root.right is not NULL
        preOrder(root.right)

In-order: left >> root >> right

ALGORITHM inOrder(root)
// INPUT <-- root node
// OUTPUT <-- in-order output of tree node's values

    if root.left is not NULL
        inOrder(root.left)

    OUTPUT <-- root.value

    if root.right is not NULL
        inOrder(root.right)

Post-order: left >> right >> root

ALGORITHM postOrder(root)
// INPUT <-- root node
// OUTPUT <-- post-order output of tree node's values

    if root.left is not NULL
        postOrder(root.left)

    if root.right is not NULL
        postOrder(root.right)

    OUTPUT <-- root.value

Breadth First

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while breadth.peek()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    if front.left is not NULL
      breadth.enqueue(front.left)

    if front.right is not NULL
      breadth.enqueue(front.right)

K-ary Trees

1. Breadth First Traversal

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while breadth.peek()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    for child in front.children
        breadth.enqueue(child)