位运算(Bit Operation):在计算机内部,数是以「二进制(Binary)」的形式表示的。位运算就是直接对数的二进制进行计算操作,在程序中使用位运算进行操作,会大大提高程序的性能。
- 二进制数(Binary):用
0和1两个数码来表示的数,它的基数是2,进位规则是「逢二进一」,借位规则是「借一当二」。例如,十进制中的1、2、3、4对应的二进制数分别为001、010、011、100。
二进制数中的每一位数字称为「位(Bit)」, 3 位所能表示的最大二进制数是 111,也就是十进制中的 7,即
在二进制的基础上,我们可以对二进制数进行相应的位运算。基本的位运算共 6 种,分别是:「按位与」、「按位或」、「按位异或」、「按位取反」、「左移」和「右移」。
按位与运算(AND):按位与运算符
&是双目运算符。其功能是对两个二进制数的每一个二进制位相与。只有对应的两个二进值位都为1时,结果位才为1。当参与运算的是负数时,参与两个数均以补码出现。
- 按位与运算规则:
1 & 1 = 11 & 0 = 00 & 1 = 00 & 0 = 0
例如,十进制中的 3 和 5 进行按位与运算,则结果如图所示:
按位与运算的通常用法:
- 清零:任何数与
0做按位与运算结果都为0。(x & 0) == 0。
- 取指定位:比如要取一个数的低
4位,则只需使用该数与二进制数00001111 (后 4 位为 1)做按位与运算,结果就是这个数的低4位的值。 - 奇偶判断:通过与
1进行按位与运算,即可判断某个数是奇数还是偶数。(x & 1) == 0为偶数,(x & 1) == 1为奇数。
按位或运算(OR):按位或运算符
|是双目运算符。其功能对两个二进制数的每一个二进制位相或。只要对应的2个二进位有一个为1时,结果位就为1。当参与运算的是负数时,参与两个数均以补码出现。
- 按位或运算规则:
1 | 1 = 11 | 0 = 10 | 1 = 10 | 0 = 0
例如,十进制中的 3 和 5 进行按位或运算,则结果如图所示:
按位或运算的通常用法:
- 将某位设置为
1:比如需要将一个数的低4位设置为1,则只需使用该数与二进制数00001111 (后 4 位为 1)做按位或运算即可得到。
按位异或运算(XOR):按位异或运算符
^是双目运算符。其功能是对两个二进制数的每一个二进制位相异或。如果某位不相同则该位为1,如果某位相同则该位为0。当参与运算的是负数时,参与两个数均以补码出现。
- 按位异或运算规则:
0 ^ 0 = 01 ^ 0 = 10 ^ 1 = 11 ^ 1 = 0
例如,十进制中的 3 和 5 进行按位异或运算,则结果如图所示:
按位异或运算的通常用法:
- 翻转指定位:比如需要将一个数的低
4位进行反转,则只需使用该数与二进制数00001111 (后 4 位为 1)做按位异或运算即可得到。 - 与
0相异或值不变:一个数与0做按位异或运算的结果不变。例如,10101100 ^ 00000000 = 10101100。 - 交换两个数:通过按位异或运算可以实现交换两个数的目的。
a, b = 10, 20
a ^= b
b ^= a
a ^= b
print(a, b)按位取反运算(NOT):按位取反运算符
~是单目运算符。其功能是对一个二进制数的每一个二进制位取反。使数字1变为0,0变为1。当参与运算的是负数时,参与的该数以补码出现。
- 按位取反运算规则:
~0 = 1~1 = 0
例如,十进制中的 3 进行按位取反运算,则结果如图所示:
按位左移运算(SHL): 按位左移运算符
<<是双目运算符。其功能是对一个二进制数的各个二进制位全部左移若干位(左边的二进制位丢弃,右边末尾补0)。
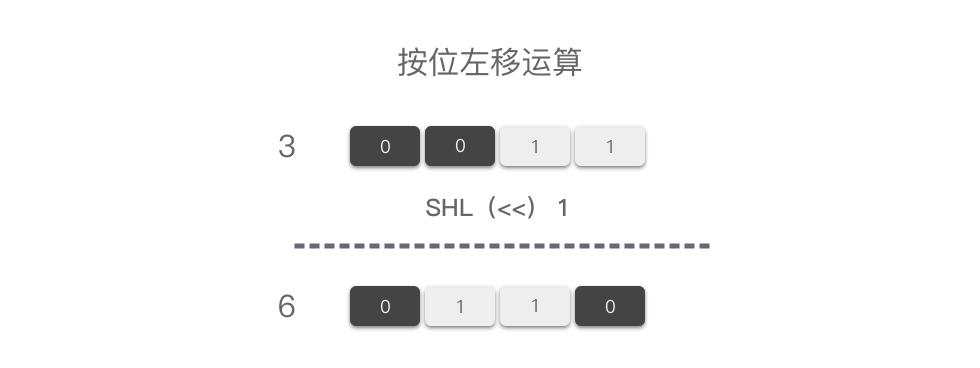
例如,十进制中的 3 进行左移 1 位运算,则结果如图所示:
按位右移运算(SHR): 按位右移运算符
>>是双目运算符。其功能是对一个二进制数的各个二进制位全部右移若干位(右边的二进制位丢弃,正数左边开补0,负数左边补1)。
例如,十进制中的 3 进行右移 1 位运算,则结果如图所示:
| 功 能 | 位运算 | 示例 |
|---|---|---|
| 去掉最后一位 | x >> 1 |
101101 -> 10110 |
在最后加一个 0 |
x << 1 |
101101 -> 1011010 |
在最后加一个 1 |
(x << 1) + 1 |
101101 -> 1011011 |
把最后一位变成 1 |
x | 1 |
101100 -> 101101 |
把最后一位变成 0 |
x | 1 - 1 |
101101 -> 101100 |
| 最后一位取反 | x ^ 1 |
101101 -> 101100 |
把右数第 k 位变成 1 |
x | (1 << (k - 1)) |
101001 -> 101101, k = 3 |
把右数第 k 位变成 0 |
x & ~(1 << (k - 1)) |
101101 -> 101001, k = 3 |
右数第 k 位取反 |
x ^ (1 << (k - 1)) |
101001 -> 101101, k = 3 |
取末尾 3 位 |
x & 7 |
1101101 -> 101 |
取末尾 k 位 |
x & 15 |
1101101 -> 1101, k = 4 |
取右数第 k 位 |
x >> (k - 1) & 1 |
1101101 -> 1, k = 4 |
把末尾 k 位变成 1 |
x | (1 << k - 1) |
101001 -> 101111, k = 4 |
末尾 k 位取反 |
x ^ (1 << k - 1) |
101001 -> 100110, k = 4 |
把右边连续的 1 变成 0 |
x & (x + 1) |
100101111 -> 100100000 |
把右边起第一个 0 变成 1 |
x | (x + 1) |
100101111 -> 100111111 |
把右边连续的 0 变成 1 |
x | (x - 1) |
11011000 -> 11011111 |
只保留右边连续的 1 |
(x ^ (x + 1)) >> 1 |
100101111 -> 1111 |
去掉右边起第一个 1 的左边 |
x & (x ^ (x - 1)) 或 x & (-x) |
100101000 -> 1000 |
从右边开始,把最后一个 1 改写成 0 |
x & (x - 1) |
100101000 -> 100100000 |