Skip to content

Latest commit

 

History

History
309 lines (196 loc) · 16.4 KB

02.Algorithm-Complexity.md

File metadata and controls

309 lines (196 loc) · 16.4 KB
Raw

1. 算法复杂度简介

算法复杂度（Algorithm complexity）：在问题的输入规模为 n 的条件下，程序的时间使用情况和空间使用情况。

「算法分析」的目的在于改进算法。

正如上文中所提到的那样：算法所追求的就是 所需运行时间更少（时间复杂度更低）、占用内存空间更小（空间复杂度更低）。所以进行「算法分析」，就是从运行时间情况、空间使用情况两方面对算法进行分析。

要比较两个算法的优劣通常有两种方法：

  • 事后统计：将两个算法各编写一个可执行程序，交给计算机执行，记录下各自的运行时间和占用存储空间的实际大小，从中挑选出最好的算法。
  • 预先估算：在算法设计出来之后，根据算法中包含的步骤，估算出算法的运行时间和占用空间。比较两个算法的估算值，从中挑选出最好的算法。

大多数情况下，我们会选择第 2 种方式。因为第 1 种方式的工作量实在太大，得不偿失。另外，即便是同一个算法，用不同的语言实现，在不同的计算机上运行，所需要的运行时间都不尽相同。所以我们一般采用预先估算的方法来衡量算法的好坏。

采用预先估算的方式下，编译语言、计算机运行速度都不是我们所考虑的对象。我们只关心随着问题规模 n 扩大时，时间开销、空间开销的增长情况。

这里的 「问题规模 n」 指的是：算法问题输入的数据量大小。对于不同的算法，定义也不相同。

  • 排序算法中：n 表示需要排序的元素数量。
  • 查找算法中：n 表示查找范围内的元素总数：比如数组大小、二维矩阵大小、字符串长度、二叉树节点数、图的节点数、图的边界点等。
  • 二进制计算相关算法中：n 表示二进制的展开宽度。

一般来说，问题的输入规模越接近，相应的计算成本也越接近。而随着问题输入规模的扩大，计算成本也呈上升趋势。

接下来，我们将具体讲解「时间复杂度」和「空间复杂度」。

2. 时间复杂度

2.1 时间复杂度简介

时间复杂度（Time Complexity）：在问题的输入规模为 n 的条件下，算法运行所需要花费的时间，可以记作为 T(n)。

我们将 基本操作次数 作为时间复杂度的度量标准。换句话说，时间复杂度跟算法中基本操作次数的数量正相关。

  • 基本操作 ：算法执行中的每一条语句。每一次基本操作都可在常数时间内完成。

基本操作是一个运行时间不依赖于操作数的操作。

比如两个整数相加的操作，如果两个数的规模不大，运行时间不依赖于整数的位数，则相加操作就可以看做是基本操作。

反之，如果两个数的规模很大，相加操作依赖于两个数的位数，则两个数的相加操作不是一个基本操作，而每一位数的相加操作才是一个基本操作。

下面通过一个具体例子来说明一下如何计算时间复杂度。

def algorithm(n):
    fact = 1
    for i in range(1, n + 1):
        fact *= i
    return fact

把上述算法中所有语句的执行次数加起来 $1 + n + n + 1 = 2n + 2$，可以用一个函数 $f(n)$ 来表达语句的执行次数：$f(n) = 2n + 2$。

则时间复杂度的函数可以表示为：$T(n) = O(f(n))$。它表示的是随着问题规模 n 的增大，算法执行时间的增长趋势跟 $f(n)$ 相同。$O$ 是一种渐进符号，$T(n)$ 称作算法的 渐进时间复杂度（Asymptotic time complexity），简称为 时间复杂度。

所谓「算法执行时间的增长趋势」是一个模糊的概念，通常我们要借助像上边公式中 $O$ 这样的「渐进符号」来表示时间复杂度。

2.2 渐进符号

「渐进符号」 实际上是专门用来刻画函数的增长速度的。简单来说，渐进符号只保留了 最高阶幂，忽略了一个函数中增长较慢的部分，比如 低阶幂、系数、常量。因为当问题规模变的很大时，这几部分并不能左右增长趋势，所以可以忽略掉。

经常用到的渐进符号有三种： $\Theta$、$O$、$\Omega$。接下来我们将一一讲解。

2.2.1 $\Theta$ 渐进紧确界符号

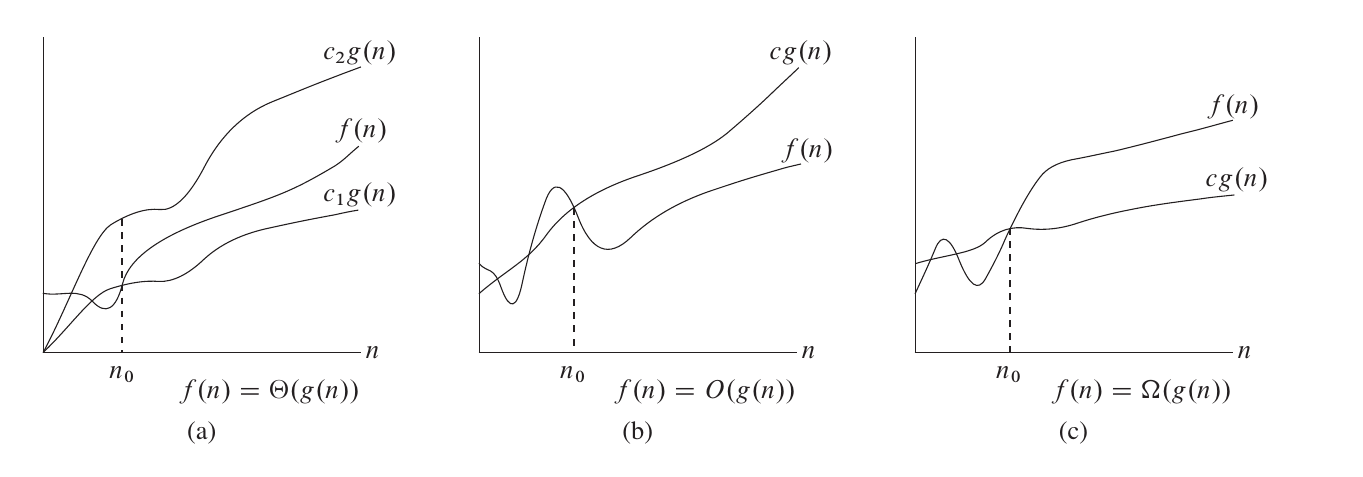
$\Theta$ 渐进紧确界符号： 对于函数 $f(n)$ 和 $g(n)$，$f(n) = \Theta(g(n))$。存在正常量 $c_1$、$c_2$ 和 $n_0$，使得对于所有 $n \ge n_0$ 时，有 $0 \le c_1 \cdot g(n) \le f(n) \le c_2 \cdot g(n)$。

也就是说，如果函数 $f(n) = \Theta(g(n))$，那么我们能找到两个正数 $c_1$、$c_2$，使得 $f(n)$ 被 $c_1 \cdot g(n)$ 和 $c_2 \cdot g(n)$ 夹在中间。

例如：$T(n) = 3n^2 + 4n + 5 = \Theta(n^2)$，可以找到 $c_1 = 1$，$c_2 = 12$，$n_0 = 1$，使得对于所有 $n \ge 1$，都有 $n^2 \le 3n^2 + 4n + 5 \le 12n^2$。

2.2.2 $O$ 渐进上界符号

$O$ 渐进上界符号： 对于函数 $f(n)$ 和 $g(n)$，$f(n) = O(g(n))$。存在常量 $c$，$n_0$，使得当 $n > n_0$ 时，有 $0 \le f(n) \le c \cdot g(n)$。

$\Theta$ 符号渐进地给出了一个函数的上界和下界，如果我们只知道一个函数的上界，可以使用 $O$ 符号。

2.2.3 $\Omega$ 渐进下界符号

$\Omega$ 渐进下界符号： 对于函数 $f(n)$ 和 $g(n)$，$f(n) = \Omega(g(n))$。存在常量 $c$，$n_0$，使得当 $n > n_0$ 时，有 $0 \le c \cdot g(n) \le f(n)$。

同样，如果我们只知道函数的下界，可以使用 $\Omega$ 符号。

2.3 时间复杂度计算

渐进符号可以渐进地描述一个函数的上界、下界，同时也可以描述算法执行时间的增长趋势。

在计算时间复杂度的时候，我们经常使用 $O$ 渐进上界符号。因为我们关注的通常是算法用时的上界，而不用关心其用时的下界。

那么具体应该如何计算时间复杂度呢？

求解时间复杂度一般分为以下几个步骤：

  • 找出算法中的基本操作（基本语句）：算法中执行次数最多的语句就是基本语句，通常是最内层循环的循环体部分。
  • 计算基本语句执行次数的数量级：只需要计算基本语句执行次数的数量级，即保证函数中的最高次幂正确即可。像最高次幂的系数和低次幂可以忽略。
  • 用大 O 表示法表示时间复杂度：将上一步中计算的数量级放入 O 渐进上界符号中。

同时，在求解时间复杂度还要注意一些原则：

  • 加法原则：总的时间复杂度等于量级最大的基本语句的时间复杂度。

如果 $T_1(n) = O(f_1(n))$，$T_2(n) = O(f_2(n))$，$T(n) = T_1(n) + T_2(n)$，则 $T(n) = O(f(n)) = max(O(f_1(n)), O(f_2(n))) = O(max(f_1(n), f_2(n)))$。

  • 乘法原则：循环嵌套代码的复杂度等于嵌套内外基本语句的时间复杂度乘积。

如果 $T_1 = O(f_1(n))$，$T_2 = O(f_2(n))$，$T(n) = T_1(n)T_2(n)$，则 $T(n) = O(f(n)) = O(f_1(n))O(f_2(n)) = O(f_1(n)f_2(n))$。

下面通过实例来说明如何计算时间复杂度。

2.3.1 常数 $O(1)$

一般情况下，只要算法中不存在循环语句、递归语句，其时间复杂度都为 $O(1)$。

$O(1)$ 只是常数阶时间复杂度的一种表示方式，并不是指只执行了一行代码。只要代码的执行时间不随着问题规模 n 的增大而增长，这样的算法时间复杂度都记为 $O(1)$。

def algorithm(n):
    a = 1
    b = 2
    res = a * b + n
    return res

上述代码虽然有 4 行，但时间复杂度也是 $O(1)$，而不是 $O(3)$。

2.3.2 线性 $O(n)$

一般含有非嵌套循环，且单层循环下的语句执行次数为 n 的算法涉及线性时间复杂度。这类算法随着问题规模 n 的增大，对应计算次数呈线性增长。

def algorithm(n):
    sum = 0
    for i in range(n):
        sum += 1
    return sum

上述代码中 sum += 1 的执行次数为 n 次，所以这段代码的时间复杂度为 $O(n)$。

2.3.3 平方 $O(n^2)$

一般含有双层嵌套，且每层循环下的语句执行次数为 n 的算法涉及平方时间复杂度。这类算法随着问题规模 n 的增大，对应计算次数呈平方关系增长。

def algorithm(n):
    res = 0
    for i in range(n):
        for j in range(n):
            res += 1
    return res

上述代码中，res += 1 在两重循环中，根据时间复杂度的乘法原理，这段代码的执行次数为 $n^2$ 次，所以其时间复杂度为 $O(n^2)$。

2.3.4 阶乘 $O(n!)$

阶乘时间复杂度一般出现在与「全排列」、「旅行商问题暴力解法」相关的算法中。这类算法随着问题规模 n 的增大，对应计算次数呈阶乘关系增长。

def permutations(arr, start, end):
    if start == end:
        print(arr)
        return
 
    for i in range(start, end):
        arr[i], arr[start] = arr[start], arr[i]
        permutations(arr, start + 1, end)
        arr[i], arr[start] = arr[start], arr[i]

上述代码中实现「全排列」使用了递归的方法。假设数组 arr 长度为 n，第一层 for 循环执行了 n 次，第二层 for 循环执行了 n - 1 次。以此类推，最后一层 for 循环执行了 1 次，将所有层 for 循环的执行次数累乘起来为 $n * (n - 1) * (n - 2) * ... * 2 * 1 = n!$ 次。则整个算法的 for 循环中基本语句的执行次数为 $n!$ 次，所以对应时间复杂度为 $O(n!)$。

2.3.5 对数 $O(log_2n)$

对数时间复杂度一般出现在「二分查找」、「分治」这种一分为二的算法中。这类算法随着问题规模 n 的增大，对应的计算次数呈对数关系增长。

def algorithm(n):
    cnt = 1
    while cnt < n:
        cnt *= 2
    return cnt

上述代码中 cnt = 1 的时间复杂度为 O(1) 可以忽略不算。while 循环体中 cnt 从 1 开始，每循环一次都乘以 2。当大于 n 时循环结束。变量 cnt 的取值是一个等比数列：$2^0，2^1，2^2，…，2^x$，根据 $2^x = n$，可以得出这段循环体的执行次数为 $log_2n$。所以这段代码的时间复杂度为 $O(log_2n)$。

2.3.6 线性对数 $O(n log_2 n)$

线性对数一般出现在排序算法中，例如「快速排序」、「归并排序」、「堆排序」等。这类算法随着问题规模 n 的增大，对应的计算次数呈线性对数关系增长。

def algorithm(n):
    cnt = 1
    res = 0
    while cnt < n:
        cnt *= 2
        for i in range(n):
            res += 1
    return res

上述代码中外层循环的时间复杂度为 $O(log_2 n)$，内层循环的时间复杂度为 $O(n)$，且两层循环相互独立，则总体时间复杂度为 $O(n log_2 n)$。

2.3.7 常见时间复杂度关系

根据从小到大排序，常见的算法复杂度主要有：$O(1)$ < $O(log_2 n)$ < $O(n)$ < $O(n log_2n)$ < $O(n^2)$ < $O(n^3)$ < $O(2^n)$ < $O(n!)$ < $O(n^n)$。

2.4 最佳、最坏、平均时间复杂度

时间复杂度是一个关于输入问题规模 n 的函数。但是因为输入问题的内容不同，习惯将「时间复杂度」分为「最佳」、「最坏」、「平均」三种情况。这三种情况的具体含义如下：

  • 最佳时间复杂度：每个输入规模下用时最短的输入所对应的时间复杂度。
  • 最坏时间复杂度：每个输入规模下用时最长的输入所对应的时间复杂度。
  • 平均时间复杂度：每个输入规模下所有可能的输入所对应的平均用时复杂度（随机输入下期望用时的复杂度）。

我们通过一个例子来分析下最佳、最坏、最差时间复杂度。

def find(nums, val):
    pos = -1
    for i in range(n):
        if nums[i] == val:
            pos = i
            break
    return pos

这段代码要实现的功能是：从一个整数数组 nums 中查找值为 val 的变量出现的位置。如果不考虑 break 语句，根据「2.3 时间复杂度计算」中讲的分析步骤，这个算法的时间复杂度是 $O(n)$，其中 n 代表数组的长度。

但是如果考虑 break 语句，那么就需要考虑输入的内容了。如果数组中第 1 个元素值就是 val，那么剩下 n - 1 个数据都不要遍历了，那么时间复杂度就是 $O(1)$，即最佳时间复杂度为 $O(1)$。如果数组中不存在值为 val 的变量，那么就需要把整个数组遍历一遍，时间复杂度就变成了 $O(n)$，即最差时间复杂度为 $O(n)$。

这样下来，时间复杂度就不唯一了。怎么办？

我们都知道，最佳时间复杂度和最坏时间复杂度都是极端条件下的时间复杂度，发生的概率其实很小。为了能更好的表示正常情况下的复杂度，所以我们一般采用平均时间复杂度作为时间复杂度的计算方式。

还是刚才的例子，在数组 nums 中查找变量值为 val 的位置，总共有 n + 1 种情况：在数组的 0 ~ n - 1 和 不在数组中。我们将所有情况下，需要执行的语句累加起来，再除以 n + 1，就可以得到平均需要执行的语句，即：$\frac{1 + 2 + 3 + ... + n + n}{n + 1} = \frac{n(n + 3)}{2(n + 1)}$。将公式简化后，得到的平均时间复杂度就是 $O(n)$。

通常只有同一个算法在输入内容不同，不同时间复杂度有量级的差距时，我们才会通过三种时间复杂度表示法来区分。一般情况下，使用其中一种就可以满足需求了。

3. 空间复杂度

3.1 空间复杂度简介

空间复杂度（Space Complexity）：在问题的输入规模为 n 的条件下，算法所占用的空间大小，可以记作为 S(n)。一般将 算法的辅助空间 作为衡量空间复杂度的标准。

除了执行时间的长短，算法所需储存空间的多少也是衡量性能的一个重要方面。而在「2. 时间复杂度」中提到的渐进符号，也同样使用于空间复杂度的度量。空间复杂度的函数可以表示为 $S(n) = O(f(n))$，它表示的是随着问题规模 n 的增大，算法所占空间的增长趋势跟 $f(n)$ 相同。

相比于算法的时间复杂度计算来说，算法的空间复杂度更容易计算，主要包括「局部变量（算法范围内定义的变量）所占用的存储空间」和「系统为实现递归（如果算法是递归的话）所使用的堆栈空间」两个部分。

以两个例子来说明。

3.1 空间复杂度计算

3.1.1 常数 O(1)

def algorithm(n):
    a = 1
    b = 2
    res = a * b + n
    return res

上述代码中使用 a、b、res 3 个局部变量，其所占空间大小并不会随着问题规模 n 的在增大而增大，所以该算法的空间复杂度为 $O(1)$。

3.1.2 线性 O(n)

def algorithm(n):
    if n <= 0:
        return 1
    return n * algorithm(n - 1)

上述代码采用了递归调用的方式。每次递归调用都占用了 1 个栈帧空间，总共调用了 n 次，所以该算法的空间复杂度为 $O(n)$。

3.1.3 常见空间复杂度关系

根据从小到大排序，常见的算法复杂度主要有：$O(1)$ < $O(log_2 n)$ < $O(n)$ < $O(n^2)$ < $O(2^n)$ 等。

算法复杂度总结

「算法复杂度」 包括 「时间复杂度」 和 「空间复杂度」，用来分析算法执行效率与输入问题规模 n 的增长关系。通常采用 「渐进符号」 的形式来表示「算法复杂度」。

常见的时间复杂度有：$O(1)$、$O(log_2 n)$、$O(n)$、$O(n log_2n)$、$O(n^2)$、$O(n^3)$、$O(2^n)$、$O(n!)$。

常见的空间复杂度有：$O(1)$、$O(log_2 n)$、$O(n)$、$O(n^2)$。

参考资料