问题描述

依据Visualizing Data using t-SNE实现t-SNE算法，并对MNIST或者Olivetti数据集进行可视化训练。

有以下几点要求：

不能使用现成的t-SNE库，例如sklearn等；
可以使用支持矩阵、向量操作的库实现，例如numpy；
将数据降低至二维，同一类型的数据使用同一种颜色绘制散点图。

符号介绍

$x_i$：第$i$个原始数据；
$y_i$：第$i$个输出数据；
$p_{j\vert i}$：输入的条件概率；
$p_{ij}$：输入的联合概率；
$q_{j\vert i}$：输出的条件概率；
$q_{ij}$：输出的联合概率；

SNE算法介绍

在SNE算法中使用高斯分布作为输入的条件分布，其条件概率定义如下： $$ \begin{equation} p_{j\vert i} = \frac{exp(-\parallel x_j - x_i\parallel^2 / (2\sigma_i^2))}{\sum_{k} exp(-\parallel x_k - x_i\parallel^2 / (2\sigma_i^2))}\quad i\ne j \tag{1} \end{equation} $$ $p_{i\vert i}$定义成0，在$(1)$的公式中，两个向量越相似（欧式距离越近）则条件概率值越大。

SNE算法中同样对低维分布进行了定义，同样选择高斯分布作为其分布，不同的是由于低维分布是经过训练得出的，我们可以事先规定其方差为1使训练过程中拟合到方差为1的结果，这样能够一定程度上简化计算，其条件概率定义如下： $$ q_{j\vert i} = \frac{exp(-\parallel y_j - y_i\parallel^2)}{\sum_{k} exp(-\parallel y_k - y_i\parallel^2)}\quad i\ne j $$ 同样地，我们将$q_{i\vert i}$定义成0。

SNE需要做的就是尽可能是这两个分布相似以达到相似的数据映射到低维时依然相似，而K-L散度可以描述两个分布的相似程度，因此SNE通过K-L散度作为其损失函数进行训练： $$ C=\sum_i\sum_j p_{j\vert i} log_2 \frac{p_{j\vert i}}{q_{j\vert i}} $$

K-L散度描述了两个分布之间的相似程度，当其值越小时两个分布则越相似。

K-L散度的一大特点是对于$p_{j\vert i}$大的而$q_{j\vert i}$小的点特别敏感，其表现为在训练过程中会尽可能让输入距离近的点在降维后距离也尽可能的近。

非对称性的影响

SNE算法中的条件概率并不具有对称性，也就是$p_{i\vert j} = p_{j\vert i}$和$q_{i\vert j} = q_{j\vert i}$并不总是成立。

这样是会存在潜在问题的：对于$i$而言，其认为$j$与其很接近（$p_{j\vert i}$比较大），在训练过程中更新$y_i$时会让其与$y_j$的距离更近，但是此时对于$j$而言，由于对称性并不一定成立，其完全可能认为$i$与其并不是很接近（$p_{i\vert j}$比较小），在训练过程中更新$y_j$时会让其与$y_i$的距离更远，这就需要更多轮数的训练才能收敛。

因此使用对称的概率密度能够获得更好的效果。

对称的概率也就类似于联合概率密度。

在t-SNE中对于高纬数据使用以下的联合分布： $$ \begin{equation} p_{ij} = \frac {p_{j\vert i} + p_{i\vert j}} {2} \tag{3} \end{equation} $$ 这样即解决了对称性的问题，同时其能保证$\sum_j p_{ij} > \frac {1} {2n}$，以免出现梯度消失的问题。

拥挤问题及解决方案

拥挤问题

对于一个高纬度，如果我们认为距离在$r$内即为相似点的话，那么对于低纬度若仍认为距离在$r$内为相似点的话，就很容易出现拥挤问题。

例如，将一个三维空间里一个半径为1的球中的点映射到二维空间里一个半径为1的圆上就很可能出现拥挤。

解决方案

根据拥挤问题产生的原因，我们只需要在衡量低维空间时，放宽距离限制。

例如，如果将一个三维空间里一个半径为1的球中的点映射到二维空间里一个半径为1的圆上很可能出现拥挤，我们不如尝试将其映射到二维空间里一个半径为2（甚至可以选择更大的半径）的圆上。

因为我们使用的是概率去衡量距离，上面的表述等价于当距离大于某个值时，若高维概率与低维概率相等，则低维概率对应的距离应该大于高维概率对应的距离。

在图像上的体现则为：从某个点开始低维概率密度函数图像一直在高维概率密度函数图像之上。

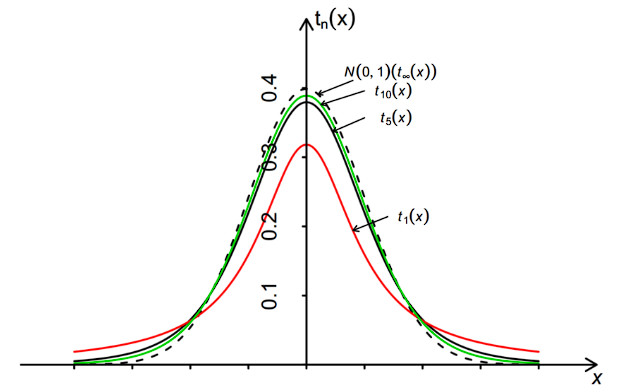
这样的概率密度函数也被称为重尾分布（这样的定义并不严谨），下图是不同自由度的t分布和高斯分布的概率密度函数：

t-SNE选择自由度为1的t分布作为低维分布，其联合分布概率定义如下： $$ \begin{equation} q_{ij} = \frac{(1 + \parallel y_i - y_j \parallel^2)^{-1}}{\sum_k \sum_{l \ne k}(1 + \parallel y_k - y_l \parallel^2)^{-1}}\quad i\ne j \tag{2} \end{equation} $$ $q_{i\vert i}$定义成0，在(2)中依然是两个向量越相似（欧式距离越近）则联合概率值越大，同时不难发现该函数关于$i, j$对称。

K-L散度则改写成如下形式： $$ C=\sum_i\sum_j p_{ij} log_2 \frac{p_{ij}}{q_{ij}} $$

梯度的计算： $$ \begin{equation} \frac{\delta C}{\delta y_i} =4\sum_j (p_{ij} - q_{ij}) (y_i - y_j) (1 + \parallel y_i - y_j \parallel^2)^{-1} \tag{4} \end{equation} $$

方差的确定

下面考虑如何计算$\sigma_i$。

$\sigma_i$可以通过困惑度来计算，困惑的表示如下： $$ \begin{aligned} &Perp(i) = 2^{H(i)} \ &H(i) = -\sum_j p_{j\vert i}log_2 p_{j\vert i} \ \end{aligned} $$ 对于某个给定的perplexity可以通过二分来确定$\sigma$（二分$\sigma_i$使其计算的$Perp(i)$与给定的perplexity接近），论文中指出perplexity一般选取5-50，而且对于perplexity的选择并不敏感。需要注意的是perplexity的选择需要小于样本个数。

perplexity实际上表明了每个点会把自己最近的多少个点看成一组，如果perplexity越大，则其会倾向于将更多的点看成一组；如果perplexity越小，则会倾向于将更少的点看成一组。因此，perplexity的选择往往会随着数据量增大而增大。

t-SNE算法流程

根据上面的分析，我们只需要对$y_i$进行初始化并进行梯度下降计算即可。算法流程大致描述如下：

计算$p_{ij}$（依据公式(3)）；
初始化$y_i$；
每轮迭代如下：
- 根据当前的$y_i$计算$q_{ij}$（依据公式(2)）；
- 计算梯度（依据公式(4)）；
- 进行梯度下降；

注意：原文中的伪代码有笔误，其中梯度下降部分的梯度前应该是减号，而不是加号，即：$y_i^{t+1} = y_i^t - \eta \frac{\delta C}{\delta y_i} + \alpha(t) (y_i^t - y_i^{t - 1})$

一些优化

学习率的优化可以使用Learning an Adaptive Learning Rate Schedule中提到的自适应调整方法；
使用动量梯度下降算法替代梯度下降算法；
eraly_exaggeration：在前50轮迭代中将p扩大4倍；
训练初期增加$L2$惩罚项；

使用随机游走改进t-SNE

使用t-SNE时，其每轮训练的复杂度是$O(n^2d)$，其中$n$是样本数量，$d$是输入数据的维度，这对于训练样本数量很多的情况下便很难处理了。一种简单的方式是随机选择总样本的一部分进行计算，但是这样不能使用到未被选择的数据。

随机游走优化的t-SNE只选择一部分数据（这一部分数据也被称为地标）进行降维可视化，但是其会利用到未被选择到的数据。

首先给出算法流程：

设输入样本个数为$N$,确定最终降维可视化的样本个数$n$，随机选择$n$个输入样本作为地标，确定邻居个数$k$；
对于$N$个输入的每一个点$i$，计算其$k$个最近的邻居节点$j$，建立$i->j$的单向边，边权为$exp(-\parallel x_i-x_j\parallel)$；
将$n$个地标的每一个点作为起点进行随机游走（随机游走过程中边被选择的概率正比于边权，也就是两个点越近走这条边的概率则越大），当且仅当其达到另一个地标点时停止随机游走，我们定义$p_{j\vert i}$表示从地标$i$开始在地标$j$停止的概率；
其余计算过程与原始t-SNE一致（将地标作为训练集）；

从上述过程中我们不难发现我们值更改了$p_{j\vert i}$的计算步骤，下面解释为什么这么做。

在上面过程的随机游走过程中，如果$p_{j\vert i}>p_{k\vert i}$说明$j, i$之间有着更多的点或者$j, i$之间的点距离更近。即使$j, k$之间的距离与$j, i$之间距离相等，我们依然会认为$j, i$更有可能是同一类点。例如下图中的例子（选择$k=3$）：

图中A, B, C距离几乎相等（甚至A, C距离更近），但是A, B中有着更多的近邻点连接，我们认为A, B是一类的点可能性更大。

上面算法的只是增加了一次全图的计算，其后续单轮训练的复杂度依然为$O(n^2d)$。

新的$p_{j\vert i}$的计算：只需要实际模拟多次随机游走计算即可。

问题分析及相关说明

问题分析

尽可能的贴近原文进行实现。其中的优化部分只有4没有实现（因为原文并没有指出前多少轮增加L2正则，而调参是一件麻烦的事情）。

因为C\C++更加贴近底层，可以使用C\C++编写t-SNE算法部分以获得更快的执行速度。

对于数据读取与处理部分可以使用torch直接实现。

对于数据可视化部分可以使用matplot绘制散点图，并使用imageio生成动态图。

超参数说明

1，2，3的实现全部依照原文，超参数的选择也尽可能的依照原文，下面是超参数说明：

learningRate：学习率，与原文一致，初始100后续按照论文中采用的优化方法进行更新；
epoch：迭代次数，与原文一致，选择1000；
perp/perplexity：困惑度，与原文一致，选择40；
alpha/momentum：动量系数，与原文设置一致，前250轮选择0.5，后续选择0.8；
exaggeration：夸大值，与原文一致，前50轮设置为4，后续设置为1；
eps：二分时的精度，原文并未给出，这里设置为1e-7；

环境说明

编译t-SNE部分需要使用cmake 3.0.0及以上的版本；
编译C++代码的编译器需要支持C++17；
数据下载、解析以及可视化部分通过Python实现；
Python 3.8及以上被要求，对应版本的numpy, imageio, matplotlib, torch, sklearn被需要；
- numpy一些基础的数据输出；
- imageio用于绘制GIF图片；
- matplotlib用于绘制每轮迭代的散点图；
- torch用于下载、解析数据。
- sklearn用于压缩原始数据；

数据集说明

与原论文一致选择用MNIST作为数据集，随机从其中抽取6000张作为数据集。

注意1：由于每轮训练的复杂度为$O(n^2d)$其中$n$是样本个数，$d$是输入数据的维度，因此在论文中训练之前使用PCA将原始数据压缩为30维。由于没有GPU的支持，我们依然选择在训练开始之前使用sklearn提供的PCA将数据压缩成30维。压缩后整个算法对于数据集需要做约1e12次计算，按照现在计算机单核每秒做1e9次运算计算的话整个计算部分的完成大约需要15分钟。实测确系15分钟左右。

注意2：在相关矩阵运算部分，容易使用多线程解决，或者使用相关的多线程矩阵计算库实现。这样对于一个八核心的计算机，理论能将运算时间降低到2~3分钟左右。但是由于C++并没有官方的包管理系统，为了保证代码的可复现性，此处不使用多线程加速。15分钟与使用GPU都需要几小时的深度网络训练时长相比实在是可以接受。

代码运行说明

如果平台是UNIK-like，在保证安装上述的环境后，直接通过bash start.sh即可执行，start.sh的流程描述如下：

首先在代码根目录创建build目录，并在build目录下通过cmake构建tsne可执行文件。
接着通过prepareData.py在代码根目录下将MNIST数据下载至data目录下，并随机读取6000个数据通过PCA进行压缩，将压缩后的数据写入data/data.in（特征）与data/label.txt（标签）中。
构建完成后，会在代码根目录下运行tsne（即在code目录下通过build/tsne运行）以确保能从相对路径中读取到数据（该过程时间较长且没有提示请耐心等待，可以通过查看data/data.out文件的大小是否发生变化来判断程序是否正常执行，程序完成时data/data.out会有六百万行的数据，可以通过查看当前的行数确定程序执行进度）。
tsne执行完成后，会继续执行createFig.py读取tsne在data/data.out中写入的1000轮低维特征y，并绘制1000张散点图放置于代码根目录下的fig目录中。散点图绘制完成后，将1000张图片组成一张GIF图片（result.gif）放置在代码根目录下。

若是Windows平台，只需要按照上述流程通过cmake构建tsne，手动执行prepareData.py，接着保证工作目录在代码根目录的情况下执行tsne二进制文件，等待执行完成后执行createDate.py即可。

代码优化说明

在公式中不乏具有对称性的公式，因此可以只计算矩阵中一半的元素，例如下面是计算输入联合概率p的代码：

for (int i = 0; i < n; i++) {
    for (int j = i + 1; j < n; j++) {
        p[i][j] = p[j][i] = max(1e-100, (output[i][j] + output[j][i]) / (2 * n)) * EXAGGERATION;
    }
}

对矩阵进行操作是尽可能的避免拷贝矩阵，例如下面是重载+=符号的代码，其直接在原矩阵上进行操作：

template<class T>
void operator+=(vector<T> &a, const vector<T> &b)
{
    for (int i = 0; i < b.size(); i++) { a[i] += b[i]; }
}

所有需要用到$\sigma_i$的地方都是以$\frac{1}{2\sigma_i^2}$形式出现，因此我们可以不计算$\sigma_i$，而是在二分时直接计算$\frac{1}{2\sigma_i^2}$，后续所有涉及$\sigma_i$第地方均进行替代，例如下面是计算输入条件概率的部分代码（其中(*doubleSigmaSquareInverse)[i]表示$\frac{1}{2\sigma_i^2}$）：

double piSum = 0;
for (int i = 0; i < x.size(); i++) {
    piSum = 0;
    for (int j = 0; j < x.size(); j++) {
        if (j == i) { continue; }
        output[i][j] = exp(-disSquare[i][j] * (*doubleSigmaSquareInverse)[i]);
        piSum += output[i][j];
    }
    for (int j = 0; j < x.size(); j++) { output[i][j] /= piSum; }
}

对于多次使用到的数据只计算一次，例如计算输入的条件概率中会使用到两个数据点之间的二范数的平方：

if (disSquare.empty()) {
    disSquare.resize(x.size(), vector<double>(x.size()));
    double normSquare = 0;
    for (int i = 0; i < x.size(); i++) {
        for (int j = i + 1; j < x.size(); j++) {
            normSquare = 0;
            assert(x[i].size() == x[j].size());
            for (int k = 0; k < x[i].size(); k++) { normSquare += pow(x[i][k] - x[j][k], 2); }
            disSquare[i][j] = disSquare[j][i] = normSquare;
        }
    }
}

代码分析

我们将t-SNE的实现放置在命名空间TSNE中，使用之前需要对以下数据进行初始化：

// n : the number of samples
// m : the dimension of every sample
// outputDimension : the dimension of result y
// epoch : the num of iterations
// perp : perplexity, usually chosen in [5, 50], and it must be less than n
// x : samples, x[i] means the i-th sample
int n, m, outputDimension, epoch;
double perp;
vector<vector<double>> x

初始化完成后即可执行run：

// run t-SNE
void run()
{
    // initialize matrixs and generate initial y
    init();
    // compute 1 / (2 sigma ^ 2)
    getDoubleSigmaSquareInverse();
    // compute joint probability pij
    auto &&output = perpNet.p(x);
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            p[i][j] = p[j][i] = max(1e-100, (output[i][j] + output[j][i]) / (2 * n)) * EXAGGERATION;
        }
    }
    // gradient descent with epoch and momentum scale
    gradientDescent(50, 0.5); 
    p /= EXAGGERATION;
    gradientDescent(200, 0.5);
    gradientDescent(epoch - 250, 0.8);
}

getDoubleSigmaSquareInverse通过二分确定$\frac {1} {2 \sigma^2}$：

while (r[0] - l[0] >= eps) {
    for (int i = 0; i < n; i++) { doubleSigmaSquareInverse[i] = (l[i] + r[i]) / 2; }
    // get Perp with now 1 / (2 sigma^2)
    auto &&perp = perpNet(x);
    for (int i = 0; i < n; i++) {
        if (perp[i] < TSNE::perp) { r[i] = doubleSigmaSquareInverse[i]; }
        else { l[i] = doubleSigmaSquareInverse[i]; }
    }
}

perpNet是一个PerpNet类的一个对象，其内部拥有PLayer, HLayer, PerpLayer三个内部类的对象p, h, perp，分别用于计算对应的公式，通过重载()实现函数式调用，以PerpLayer的operator()代码为例：

vector<double> & operator()(const vector<double> x)
{
    if (output.empty()) { output.resize(x.size()); }
    for (int i = 0; i < x.size(); i++) { output[i] = pow(2, x[i]); }
    return output;
}

下面给出gradientDescent部分的部分代码：

// calculate joint probability of current result y
q = &qLayer(y);
// calculate gradient
getGradient();
fill(ymean.begin(), ymean.end(), 0);
for (int i = 0; i < n; i++) {
    for (int d = 0; d < outputDimension; d++) {
        // update learning rate adaptively
        // we don't update learningRate variable; we use learningRate * gain[i][d] as the new learning rate
        gain[i][d] = max(sign(g[i][d]) == sign(lastY[i][d]) ? gain[i][d] * 0.8 : gain[i][d] + 0.2, 0.01);
        // get step
        step = momentum * (y[i][d] - lastY[i][d]) - learningRate * gain[i][d] * g[i][d];
        lastY[i][d] = y[i][d];
        y[i][d] += step;
        // for centralization
        ymean[d] += y[i][d];
    }
}
for (int d = 0; d < outputDimension; d++) { ymean[d] /= n; }
// centralization
for (int i = 0; i < n; i++) {
    for (int d = 0; d < outputDimension; d++) {
        y[i][d] -= ymean[d];
    }
}
// output y after every iteration
cout << y;

梯度计算部分的代码：

for (int i = 0; i < n; i++) {
    fill(g[i].begin(), g[i].end(), 0);
    for (int j = 0; j < n; j++) {
        // this scale is to prevent re-calculation
        scale = 4 * (p[i][j] - (*q)[i][j]) * qLayer.disSquarePlusInverse[i][j];
        for (int d = 0; d < outputDimension; d++) { g[i][d] += scale * (y[i][d] - y[j][d]); }
    }
}

详细的代码可以查看code/tsne.cpp。

注意：由于写报告时，没有增加随机游走的实现，所以上述的代码分析是按照没有随机游走代码时的版本进行分析，而后续实现随机游走后合并了一些代码以方便复用，可能结构上会有所不同，但是非随机游走部分执行与上述分析过程一致。

实验结果

我同样实现了随机游走版本的t-SNE由于不是作业的要求没有给出代码分析部分，这里只给出某次实验的结果。

某次随机实验的结果如下(可通过右键在新标签页打开以重新播放)：

普通版本：由于图片不能超过5MB，所以你只能通过连接自行查看：result.gif
随机游走版本：由于图片不能超过5MB，所以你只能通过连接自行查看：result_random_walk.gif

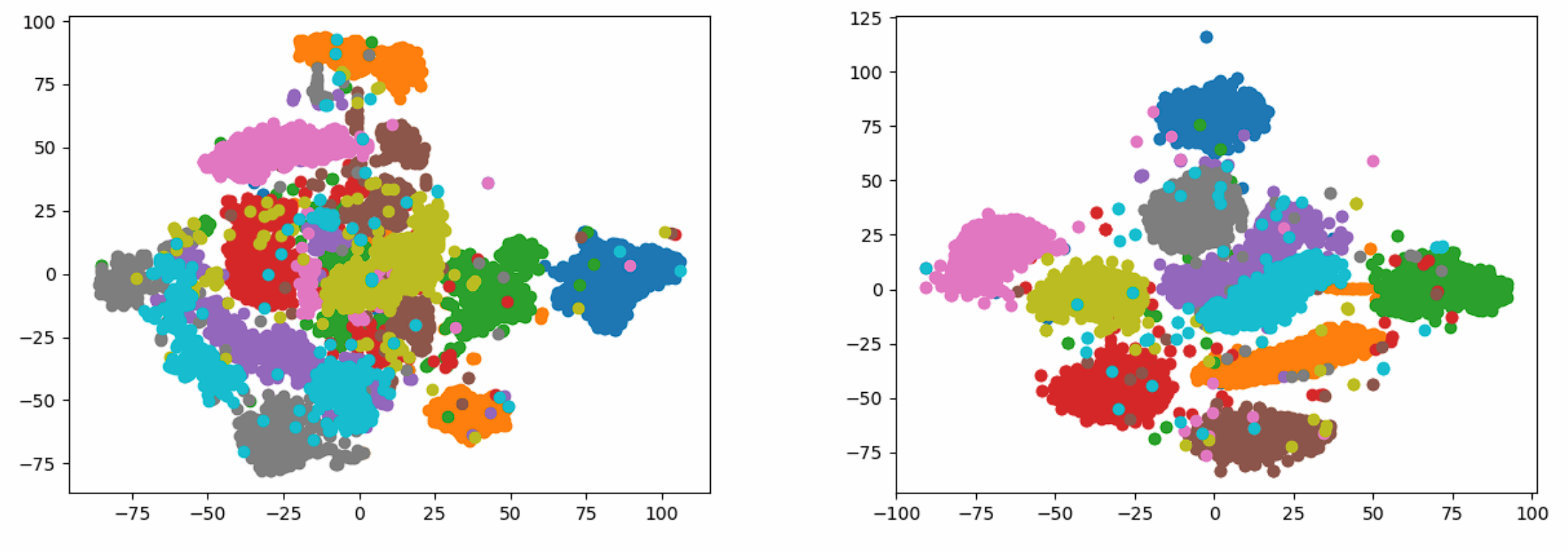
提供最终结果的静态图（左侧普通版本，右侧随机游走版本）：补充一点运行时间（单核运行）：普通版本：

time of getDisSquare: 0.406387 (s)
time of randomSelection: 0.0014 (s)
time of getDoubleSigmaSquareInverse: 34.677 (s)
time of calculating joint probability: 35.357 (s)
time of run t-SNE: 736.599 (s)

随机游走：

time of getDisSquare: 71.0614 (s)
time of randomSelection: 0.007075 (s)
time of getKNearestNeighbor for all nodes: 7.71446 (s)
time of calculating joint probability with random walk: 100.894 (s)
time of run t-SNE: 903.163 (s)

引用

Learning an Adaptive Learning Rate Schedule

Visualizing Data using t-SNE

最后的话

代码仓库：Kaiser-Yang/t-SNE。

后续如果有时间，我可能会自己去实现多线程的矩阵乘法（别问我为什么要自己实现多线程矩阵乘法，Just for fun）试着对比一下多线程与单线程的运行时间。

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

tsneIntroduction.md

tsneIntroduction.md

问题描述

符号介绍

SNE算法介绍

非对称性的影响

拥挤问题及解决方案

拥挤问题

解决方案

方差的确定

t-SNE算法流程

一些优化

使用随机游走改进t-SNE

问题分析及相关说明

问题分析

超参数说明

环境说明

数据集说明

代码运行说明

代码优化说明

代码分析

实验结果

引用

最后的话

Files

tsneIntroduction.md

Latest commit

History

tsneIntroduction.md

File metadata and controls

问题描述

符号介绍

SNE算法介绍

非对称性的影响

拥挤问题及解决方案

拥挤问题

解决方案

方差的确定

t-SNE算法流程

一些优化

使用随机游走改进t-SNE

问题分析及相关说明

问题分析

超参数说明

环境说明

数据集说明

代码运行说明

代码优化说明

代码分析

实验结果

引用

最后的话