def isUnique(self, astr):
s = set(astr)
return len(s) == len(astr)def isUnique(self, astr):
for i in range(len(astr)):
if astr[i] in astr[i+1:]:
return False
return Truecheck astr[i] in astr[i+1:] is also using nested for under the hood.
def isUnique(self, astr):
arr = [0] * 26
for i in range(len(astr)):
index = ord(astr[i]) - ord('a')
if arr[index] == 1:
return False
else:
arr[index] += 1
return TrueWhenever there is bool array, we can consider using bit to save space.
We can use an integer 0, which has 32 bits, we use its right 26 bits as markers. First we need to know 1 << 4 we get ...0001000, 1 << 6 we get ...000100000, so first we calculate the binary of each character by c - 'a', then shift it, do & with current. if result is not 0, then there is duplication, other wise we update markers by | with current makers.
def isUnique(self, astr: str) -> bool:
mark = 0
for char in astr:
move_bit = ord(char) - ord('a')
if (mark & (1 << move_bit)) != 0:
return False
else:
mark |= (1 << move_bit)
return Truedef CheckPermutation(self, s1, s2):
return ''.join(sorted(s1)) == ''.join(sorted(s2))def CheckPermutation(self, s1, s2):
if len(s1) != len(s2):
return False
arr = [0] * 52
for i in range(len(s1)):
arr[ord(s1[i]) - ord('a')] += 1
for i in range(len(s2)):
arr[ord(s2[i]) - ord('a')] -= 1
return all(v == 0 for v in arr)def replaceSpaces(self, S: str, length: int) -> str:
return S[:length].replace(' ','%20')public String replaceSpaces(String S, int length) {
char[] ch = new char[length * 3];
int index = 0;
for (int i = 0; i < length; i++) {
char c = S.charAt(i);
if (c == ' ') {
ch[index++] = '%';
ch[index++] = '2';
ch[index++] = '0';
} else {
ch[index] = c;
index++;
}
}
return new String(ch, 0, index);
}public String replaceSpaces(String S, int length) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < length; i++) {
char ch = S.charAt(i);
if (ch == ' ') {
sb.append("%20");
continue;
}
sb.append(ch);
}
return sb.toString();
}count the number of each character, the numbers can only have 1 odd number at most.
def canPermutePalindrome(self, s):
count = [i for i in Counter(s).values() if i%2 != 0]
return len(count) <= 1
# return sum(1 for k, v in collections.Counter(s).items() if v % 2 != 0) <= 1In Java, there is no convenient way to count the number of each character, so we can only use hashmap or character array to count.
public boolean canPermutePalindrome(String s) {
char[] chars = s.toCharArray();
int[] target = new int[128];
for (char c : chars) {
target[c] += 1;
}
int count = 0;
for (int i : target) {
if(i % 2 != 0) {
count++;
}
if(count > 1) {
return false;
}
}
return true;
}When we are checking if something appear even times, we can use set: if set contains current element, then remove it from set, if set doesn't contain current element, put it into set, finally check if the set is empty.
public boolean canPermutePalindrome(String s) {
Set<Character> set = new HashSet<>();
for(int i = 0; i < s.length(); i++){
if(set.contains(s.charAt(i))){
set.remove(s.charAt(i));
}else{
set.add(s.charAt(i));
}
}
return set.size() < 2;
}leetcode and leettode, the first difference is c and t, we compare ode and ode.
leetcode and leetode, we keep the first string longer, the first difference is c and o, we compare ode with ode.
def oneEditAway(self, first, second):
if abs(len(first) - len(second)) >1:
return False
if len(first) < len(second): //guarantee first is longer than second
return self.oneEditAway(second, first)
for i in range(len(second)):
if first[i] != second[i]:
if len(first) == len(second):
return first[i+1:] == second[i+1:] //leetcode and leettode
return first[i+1:] == second[i:] //leetcode and leetode
return TrueTwo pointers compare from two ends, if different, they stop, then compare the length of the rest of string
The first pointer stop at the first difference, second pointer stops at second difference, if they are the same difference(rest string length is 1), then return true. Otherwise return false.
leetcode and leettode, first pointer stop at t, second pointer stop at o, two pointer difference < 1, return true
leetcode and leetode, first pointer stop at t, second pointer stop at o, two pointer difference < 1, return true.
public:
bool oneEditAway(string first, string second) {
if(first==second){
return true;
}
const int len1=first.size();
const int len2=second.size();
if(abs(len1-len2)>1){
return false;
}
int i=0,j=len1-1,k=len2-1;
while(i<len1 && i<len2 && first[i]==second[i]){ // i从左至右扫描
++i;
}
while(j>=0 && k>=0 && first[j]==second[k]){ // j、k从右至左扫描
--j;
--k;
}
return j-i<1 && k-i<1;
}Nothing but count
def compressString(self, S: str) -> str:
if not S:
return ""
ch = S[0]
ans = ''
cnt = 0
for c in S:
if c == ch:
cnt += 1
else:
ans += ch + str(cnt)
ch = c
cnt = 1
ans += ch + str(cnt)
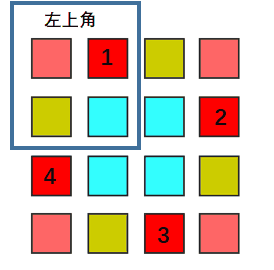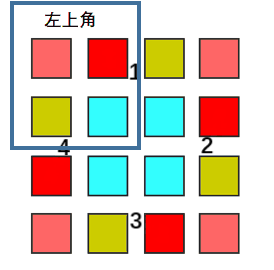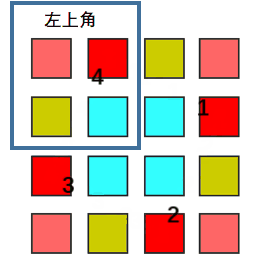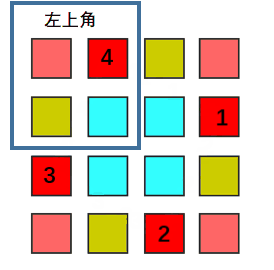
return ans if len(ans) < len(S) else Sn is even:
n is odd:
So whatever n is even or odd, we only iterate the left corner part, rotate every element of that part with other three parts.
def rotate(self, matrix):
n = len(matrix)
for i in range(n//2):
for j in range((n+1)//2):
matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] \
= matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]Or we can vertically revers, then diagonal reverse:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
# 水平翻转
for i in range(n // 2):
for j in range(n):
matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
# 主对角线翻转
for i in range(n):
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]First, we cannot change the elements in place when we are iterating the matrix, because after we modify the elements, the matrix got changed.
We can use two array to store the row and column number that has 0 in the first iteration, then iterate the matrix again, set corresponding row and column 0.
def setZeroes(self, matrix: List[List[int]]) -> None:
row=set()
column=set()
for i in range(len(matrix)):
for j in range(len(matrix[0])):
if matrix[i][j]==0:
row.add(i)
column.add(j)
for i in row:
for j in range(len(matrix[0])):
matrix[i][j]=0
for j in column:
for i in range(len(matrix)):
matrix[i][j]=0
returnBut if we cannot use extra array to store the row and column number, we must find another place to store the row and column.
The answer is the first row and column elements. We use them to store the information of corresponding row and column.
But because we are modifying first column and row, so we need to store whether the first row and column has 0.
def setZeroes(self, matrix):
first_row = False
first_col = False
#check if first row has 0
for i in matrix[0]:
if i == 0:
first_row = True
#check if first column has 0
for i in range(len(matrix)):
if matrix[i][0] == 0:
first_col = True
#if that element is 0, set that first row and first column as 0
for i in range(1, len(matrix)):
for j in range(1, len(matrix[0])):
if matrix[i][j] == 0:
matrix[0][j] = 0
matrix[i][0] = 0
#if that first row or first column is 0, set that row or column as 0
for i in range(1, len(matrix)):
for j in range(1, len(matrix[0])):
if matrix[0][j] == 0 or matrix[i][0]==0:
matrix[i][j] =0
#if first col has 0, set all elements of first column as 0
if first_col:
for i in range(len(matrix)):
matrix[i][0] = 0
#if first row has 0, set all elements of first row as 0
if first_row:
for i in range(len(matrix[0])):
matrix[0][i] = 0First, consider if they are the same length.
If the same length, repeat any one of them, the new string must contain the other one.
def isFlipedString(self, s1, s2):
if len(s1) != len(s2):
return False
s = s2 + s2
return s1 in sNote that head is the head of a linked list, so we have to iterate the list by head = head.next
The idea is put all occurred value into a set, if already contain the value, skip the node.
def removeDuplicateNodes(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if not head:
return head
occurred = {head.val}
pos = head
# 枚举前驱节点
while pos.next:
# 当前待删除节点
cur = pos.next
if cur.val not in occurred:
occurred.add(cur.val)
pos = pos.next
else:
pos.next = pos.next.next
return headdef kthToLast(self, head, k):
if not head:
return head
fast = head
slow = head
while fast.next and k > 1:
fast = fast.next
k-=1
while fast.next:
fast = fast.next
slow = slow.next
return slow.valpublic int kthToLast(ListNode head, int k) {
Stack<ListNode> stack = new Stack<>();
//链表节点压栈
while (head != null) {
stack.push(head);
head = head.next;
}
//在出栈串成新的链表
ListNode firstNode = stack.pop();
while (--k > 0) {
ListNode temp = stack.pop();
temp.next = firstNode;
firstNode = temp;
}
return firstNode.val;
}Whenever there is singly linked list, we should think about recursion.
Recursion is referring Go and Back. Go is because function call, back is because function return.
So we want kth to last element, we can have a global variable start from 0 at the last node, then back to increase till it is equal to k.
def kthToLast(self, head, k):
if head is None:
return 0
n = self.kthToLast(head.next, k)
self.count += 1
return head.val if self.count == k else nThe recursion return process means, if count == k, I return head.val, otherwise, I return what I get from may next recursion. The whole process only two function return it selves value, the last one(0), and the count == k one(head.val). And the head.val replaced the 0.
Manipulate singly linked list, sometimes we may don't change the list, but only change the value.
def deleteNode(self, node):
node.val = node.next.val
node.next = node.next.nextThis is the idea of quick sort, we partition the list according to a pivotal.
The idea of quick sort partition is that, two pointer p1 and p2, p1 is reserved for all smaller values than pivotal, p2 is go ahead to find smaller values, if no found, p2 continue moving on, if found, p2 swap value with p1, then p1 and p2 both moving next. Until p2 reach the end.
def partition(self, head, x):
if not head: return head
p, q = head, head
while q:
if q.val < x:
q.val, p.val = p.val, q.val
p = p.next
q = q.next
return headAbove code is doing Node swapping by swapping the value.
Another straightforward solution is we create two Linked list, the first one link the smaller nodes, the second link the bigger nodes. and finally, we put the bigger list after the smaller list.
Example
Input(7 -> 1 -> 6) + (5 -> 9 -> 2),即617 + 295 Output2 -> 1 -> 9,即912
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
head = ListNode(0)
node = head
carry = 0
while l1 or l2:
if l1 == None:
node.next = l2
l1 = ListNode(0)
if l2 == None:
node.next = l1
l2 = ListNode(0)
sum_up = carry + l1.val + l2.val
node.next = ListNode(sum_up % 10)
carry = sum_up // 10
node = node.next
l1 = l1.next
l2 = l2.next
if carry:
node.next = ListNode(carry)
return head.nextNote that if one of list is longer, we use 0 to make up.
Advanced: Suppose the digits are stored in forward order. Repeat the above problem:
Input:(6 -> 1 -> 7) + (2 -> 9 -> 5),即617 + 295 Output:9 -> 1 -> 2,即912
Here we can use recursion, but recursion is difficult to understand, so I am using another straightforward way, we convert each list to a number, sum them, the convert back to a list.
def addTwoNumbers(self, l1, l2):
# two array to store the fetched integer
list1 = []
list2 = []
# populate the list with numbers
self.add(list1, l1)
self.add(list2, l2)
# calculate the value of the number
num1 = self.getNumberFromList(list1)
num2 = self.getNumberFromList(list2)
# calculate the sum
s = num1 + num2
# convert the sum to a linked list
head = ListNode(-1)
result = ListNode(s % 10)
head.next = result
r = s // 10
while r != 0:
temp = head.next
head.next = ListNode(r % 10)
head.next.next = temp
r = r // 10
return head.next
def getNumberFromList(self, list) -> int:
weight = 1
num1 = 0
for i in list1[::-1]:
num1 += weight * i
weight *= 10
return num1
def add(self, list, linkedList):
if not linkedList:
return
self.add(list, linkedList.next)
list.append(linkedList.val)
returnTake advantage of other data structure.
For palindrome, reverse it, we can get the same as original list.
def isPalindrome(self, head):
stack = []
temHead = head
while temHead:
stack.append(temHead.val)
temHead = temHead.next
while head:
if head.val != stack.pop():
return False
head = head.next
return TrueUsing stack has a O(n) space complexity, we can do better.
First, using two pointers to find the middle of the linked list. Second, reverse the later half. Third, compare the first part with second part, check if they are the same.
def isPalindrome(self, head):
faster = head
slower = head
# find the middle
while faster and faster.next:
faster = faster.next.next
slower = slower.next
# If number is odd, we take the next of the middle
if faster:
slower = slower.next
faster = head
# reverse the second part
pre = None
while slower:
nex = slower.next
slower.next = pre
pre = slower
slower = nex
# compare the second part with the first part
while pre:
if faster.val != pre.val:
return False
pre = pre.next
faster = faster.next
return TrueWe are checking if the set already has the object, we can use a HashSet, if hash method is not overrode, the default is comparing "==", the address of the object, which is exactly the identity of the object.
def getIntersectionNode(self, headA, headB):
se = set()
while headA:
se.add(headA)
headA = headA.next
while headB:
if headB in se:
return headB
headB = headB.next
return NoneTwo pointers A and B, A iterate from headA, after reaching the end, switch to headB. B iterate from headB, after reaching the end, switch to headA. A and B will meet at the intersection. If headA and headB don't intersect, A and B will meet at null.
def getIntersectionNode(self, headA, headB):
pointer1 = headA
pointer2 = headB
while pointer1 != pointer2:
pointer1 = headB if pointer1 is None else pointer1.next
pointer2 = headA if pointer2 is None else pointer2.next
return pointer1def detectCycle(self, head):
my_set = set()
cursor = head
while cursor:
if cursor in my_set:
return cursor
my_set.add(cursor)
cursor = cursor.next
return NoneIf there is cycle, they will meet, then move faster to head, move them one step once, till they meet again, that the intersection.
def detectCycle(self, head):
faster = head
slower = head
while faster and faster.next:
faster = faster.next.next
slower = slower.next
if faster == slower:
faster = head
while faster != slower:
faster = faster.next
slower = slower.next
return faster
return NoneIf implement two stacks with one array, we can grow two stacks from two ends. So that we can make full use of the stack.
Now we are asked to implement three stacks with one array, and it tells us the size of the stack, so we can create an array with three times of the stack, and grow them individually.
But I am going to use another way, three stacks can be stored into three some spaces, stack0 occupy 0,3,6,9..., stack1 occupy 1,4,7..., stack2 occupy 2,5,8..., for convenience, we can use position 0,1,2 to store the corresponding next position of the stacks. the real elements start from 3,4,5.
def __init__(self, stackSize):
"""
:type stackSize: int
"""
self.arr = [None] * (stackSize*3+3)
self.size = stackSize
self.arr[0] = 3
self.arr[1] = 4
self.arr[2] = 5
def push(self, stackNum, value):
"""
:type stackNum: int
:type value: int
:rtype: None
"""
if self.arr[stackNum] // 3 > self.size:
return
self.arr[self.arr[stackNum]] = value
self.arr[stackNum] += 3
def pop(self, stackNum):
"""
:type stackNum: int
:rtype: int
"""
if self.arr[stackNum] < 6:
return -1
self.arr[stackNum] -= 3
res = self.arr[self.arr[stackNum]]
self.arr[self.arr[stackNum]] = None
return res
def peek(self, stackNum):
"""
:type stackNum: int
:rtype: int
"""
if self.arr[stackNum] < 6:
return -1
res = self.arr[self.arr[stackNum]-3]
return res
def isEmpty(self, stackNum):
"""
:type stackNum: int
:rtype: bool
"""
return self.arr[stackNum] < 6def __init__(self):
"""
initialize your data structure here.
"""
self.stack = []
self.min_stack = []
def push(self, x):
"""
:type x: int
:rtype: None
"""
if self.min_stack and self.min_stack[-1] < x:
self.min_stack.append(self.min_stack[-1])
self.stack.append(x)
return
self.stack.append(x)
self.min_stack.append(x)
def pop(self):
"""
:rtype: None
"""
if len(self.min_stack) == 0:
return
self.min_stack.pop()
return self.stack.pop()
def top(self):
"""
:rtype: int
"""
if len(self.min_stack) == 0:
return
return self.stack[-1]
def getMin(self):
"""
:rtype: int
"""
return self.min_stack[-1]The idea is keeping track of the extreme values:
The tricky part is some special boundary case.
def __init__(self, cap):
"""
:type cap: int
"""
self.cap = cap
self.set = []
def push(self, val):
"""
:type val: int
:rtype: None
"""
# 如果初始容量小于0 直接return
if self.cap <= 0:
return
if len(self.set) == 0 or len(self.set[-1]) >= self.cap:
# 当栈满了,或没有栈了,则新建一个栈
self.set.append([val])
else:
self.set[-1].append(val)
def pop(self):
"""
:rtype: int
"""
if len(self.set) == 0:
return -1
res = self.set[-1].pop()
if len(self.set[-1]) == 0:
# 如果pop后栈为空,则删除该栈
self.set.pop()
return res
def popAt(self, index):
"""
:type index: int
:rtype: int
"""
if len(self.set) <= index:
return -1
res = self.set[index].pop()
if len(self.set[index]) == 0:
# 如果pop后栈为空,则删除该栈
self.set.remove(self.set[index])
return respush is doing A.push()
pop is doing B.pop()
Whenever B is empty, push all A to B. Don't have to switch upside down for every push and pop.
def __init__(self):
"""
Initialize your data structure here.
"""
self.pushs = []
self.pops = []
def push(self, x):
"""
Push element x to the back of queue.
:type x: int
:rtype: None
"""
self.pushs.append(x)
def pop(self):
"""
Removes the element from in front of queue and returns that element.
:rtype: int
"""
if len(self.pops) == 0:
for i in range(len(self.pushs)):
self.pops.append(self.pushs.pop())
return self.pops.pop()
def peek(self):
"""
Get the front element.
:rtype: int
"""
if len(self.pops) == 0:
for i in range(len(self.pushs)):
self.pops.append(self.pushs.pop())
temp = self.pops.pop()
self.pops.append(temp)
return temp
def empty(self):
"""
Returns whether the queue is empty.
:rtype: bool
"""
if len(self.pushs)==0 and len(self.pops)==0:
return True
else:
return FalseWhenever push a new element, find the first bigger element by popping to another assistant stack. then push back to the main stack.
def __init__(self):
self.stack = []
def push(self, val):
"""
:type val: int
:rtype: None
"""
if len(self.stack) == 0 or self.stack[-1] >= val:
self.stack.append(val)
return
else:
temp = []
while len(self.stack) != 0 and self.stack[-1] < val:
temp.append(self.stack.pop())
self.stack.append(val)
while temp:
self.stack.append(temp.pop())
def pop(self):
"""
:rtype: None
"""
return self.stack.pop() if len(self.stack) != 0 else -1
def peek(self):
"""
:rtype: int
"""
return self.stack[-1] if len(self.stack) != 0 else -1
def isEmpty(self):
"""
:rtype: bool
"""
return len(self.stack) <= 0Every time we push, we have to move some elements to temporary stack, then move them back. Some times we don't have to move them back right away.
- If new element is bigger than main stack top, then pop main stack to temporary stack until find a bigger top, then push new element to main stack. At this time, we don't have to move temporary stack back.
- If new element is smaller than main stack but bigger than temporary stack top, just push new element to temporary stack.
- If new element is smaller than main stack top, and smaller than temporary stack top, then move temporary stack to main stack until find a top smaller than new element, push new element to temporary stack.
Above way saves run time, but code become complex.
Two queue, one cat, one dog, compare the sequence number of the first elements of two queue, get oldest animal. If any queue is empty, try another one.
def __init__(self):
self.a = [deque(), deque()]
def enqueue(self, animal):
self.a[animal[1]].append(animal)
def dequeueAny(self):
if self.a[0] and self.a[1]:
# 这里是一种三元操作符,第一个判断是真的话,返回or前面的值,假的话,返回or后面的直
return self.a[0][0][0] < self.a[1][0][0] and self.a[0].popleft() or self.a[1].popleft()
return self.a[0] and self.dequeueCat() or self.dequeueDog()
def dequeueDog(self):
return self.a[1] and self.a[1].popleft() or [-1, -1]
def dequeueCat(self):
return self.a[0] and self.a[0].popleft() or [-1, -1]def findWhetherExistsPath(self, n, graph, start, target):
next_level = set()
next_level.add(start)
while len(next_level) != 0:
nexts = set()
for g in graph:
if g[0] in next_level:
if g[1] == target:
return True
nexts.add(g[1])
next_level = nexts
return FalseNote for next level, we are using a set, because we only want to check if the node is a node we want to check, so using a set improve the speed of checking. If we use a list, the time will exceed.
Because a binary search tree means root is bigger than left, smaller than right. Now we have a sorted array, if we do binary iterate, every time we use left side as left child, right side as right child, this satisfy the feature of binary tree. Furthermore, we want the tree balance, binary iterating will split the array almost equally, so the tree will be balanced.
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
return self.buildTree(0, len(nums)-1, nums)
def buildTree(self, start, end, nums):
if start > end:
return None
mid = (end - start+1) // 2 + start
root = TreeNode(nums[mid])
root.left = self.buildTree(start, mid-1, nums)
root.right = self.buildTree(mid+1, end, nums)
return rootAbove can be more precise:
def sortedArrayToBST(self, nums: List[in]) -> TreeNode:
if not nums:
return
mid = len(nums) // 2
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(nums[: mid])
root.right = self.sortedArrayToBST(nums[mid + 1: ])
return root With minimal height means avoid null node before the last layer, this can be satisfied by binary search on sorted array.
Note the output is a node linked list, when we are layered iterating tree, we have to create linked list for each layer, and add its list head to the result list.
def listOfDepth(self, tree: TreeNode) -> List[ListNode]:
next_layer = [tree]
res = []
layer_list = ListNode(-1)
layer_list.next = ListNode(tree.val)
while next_layer:
res.append(layer_list.next)
temp = []
layer_list = ListNode(-1)
cursor = layer_list
for node in next_layer:
if node.left:
temp.append(node.left)
cursor.next = ListNode(node.left.val)
cursor = cursor.next
if node.right:
temp.append(node.right)
cursor.next = ListNode(node.right.val)
cursor = cursor.next
next_layer = temp
return resWhen traverse the tree, we can define a level to record the level information.
def listOfDepth(self, tree: TreeNode) -> List[ListNode]:
ans = []
def dfs(node, level):
if not node: return None
if len(ans) == level:
ans.append(ListNode(node.val))
else:
head = ListNode(node.val)
head.next = ans[level]
ans[level] = head
dfs(node.right, level + 1)
dfs(node.left, level + 1)
dfs(tree, 0)
return ansdef isBalanced(self, root: TreeNode) -> bool:
if not root:
return True
left_height = self.__getHeight(root.left, 0)
right_height = self.__getHeight(root.right, 0)
if abs(left_height - right_height) > 1:
return False
return self.isBalanced(root.left) and self.isBalanced(root.right)
def __getHeight(self, root, height):
if not root:
return height
left_height = self.__getHeight(root.left, height+1)
right_height = self.__getHeight(root.right, height+1)
return max(left_height, right_height)Above code can be more precise:
def isBalanced(self, root: TreeNode) -> bool:
# 空树是平衡树
if not root:
return True
# 若左右子树深度超过1,非AVL
if abs(self.__getHeight(root.left) - self.__getHeight(root.right)) > 1:
return False
# 递归执行,当出现不满足AVL性质的子树时,执行短路运算立即返回结果
return self.isBalanced(root.left) and self.isBalanced(root.right)
# 计算以当前节点为根的树深度
def __getHeight(self, root: TreeNode) -> int:
if root:
return 1 + max(self.__getHeight(root.left), self.__getHeight(root.right))
return 0pre = None
def isValidBST(self, root: TreeNode) -> bool:
if not root:
return True
l = self.isValidBST(root.left)
if self.pre and self.pre.val >= root.val:
return False
self.pre = root
r = self.isValidBST(root.right)
return l and rdef isValidBST(self, root: TreeNode) -> bool:
stack = []
p = root
res = []
while p or stack :
while p:
stack.append(p)
p = p.left
if stack :
node = stack.pop()
res.append(node.val)
p = node.right
return res == sorted(set(res))Because it's a binary search tree, we are searching the next element greater than p.val
If current value greater than p, we go to left tree of current, at the same time, we store current node(father node of next node).
If current value smaller than p, we go to right tree of current.
def inorderSuccessor(self, root: TreeNode, p: TreeNode) -> TreeNode:
res = None
cur = root
while cur:
if cur.val <= p.val:
cur = cur.right
else:
res = cur
cur = cur.left
return res- If reach p or q, return the node to its parent
- Get left and right child of current node.
- If left is null, means all p and q are in right, right node is their first common parent
- If right is null, means all p and q are in left, left node is their first common parent
- If neither right nor left are null, means we found p and q in two side, current node is their first common parent.
Note: The function only return the node p or q, Or the node that have p and q on left and right. So the returned node is the first common node, it cannot be override. There is only one node that p and q reside two sides of it.
def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
if not root or root.val == p.val or root.val == q.val:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
#如果left为空,说明这两个节点在cur结点的右子树上,我们只需要返回右子树查找的结果即可
if not left:
return right
#同上
if not right:
return left
# 如果left和right都不为空,说明这两个节点一个在cur的左子树上一个在cur的右子树上,我们只需要返回cur结点即可。
return rootIf both pre-order and post-order contains the smaller tree, then smaller tree is subtree
def checkSubTree(self, t1: TreeNode, t2: TreeNode) -> bool:
def preOder(t, t_pre_order):
if not t:
return t_pre_order
t_pre_order.append(t.val)
preOder(t.left, t_pre_order)
preOder(t.right, t_pre_order)
return t_pre_order
def postOder(t, t_post_order):
if not t:
return t_post_order
postOder(t.left, t_post_order)
postOder(t.right, t_post_order)
t_post_order.append(t.val)
return t_post_order
t1_pre_order = preOder(t1, [])
t2_pre_order = preOder(t2, [])
t1_post_order = postOder(t1, [])
t2_post_order = postOder(t2, [])
return ''.join([str(i) for i in t2_pre_order]) in ''.join([str(i) for i in t1_pre_order]) and ''.join(
[str(i) for i in t2_post_order]) in ''.join(str(i) for i in t1_post_order)Above algorithm is slow
def checkSubTree(self, t1: TreeNode, t2: TreeNode) -> bool:
# If t1 t2 is None, return true, otherwise, return false.
# If t2 is none, t1 is not, it will be determine by isSame, return false
if not t1:
return t2 is None
return self.isSame(t1, t2) or self.checkSubTree(t1.left, t2) or self.checkSubTree(t1.right, t2)
def isSame(self, root1, root2):
if not root1 and root2:
return True
if not (root1 and root2):
return False
if root1.val != root2.val:
return False
return self.isSame(root1.left, root2.left) and self.isSame(root1.right, root2.right)First layer traverse is normal traverse, for each node, do the second layer traverse, it is back tracking to calculate the sum.
def __init__(self) -> None:
self.count = 0
def pathSum(self, root: TreeNode, sum: int) -> int:
if not root:
return self.count
self.backTracking(root, 0, sum)
self.pathSum(root.left, sum)
self.pathSum(root.right, sum)
return self.count
def backTracking(self, rot, temSum, sum):
if not rot:
return
temSum += rot.val
if temSum == sum:
self.count += 1
self.backTracking(rot.left, temSum, sum)
self.backTracking(rot.right, temSum, sum)
returndef insertBits(self, N: int, M: int, i: int, j: int) -> int:
if N <= M: return M
sum_i = 0
for t in range(i):
sum_i += 2 ** t
sum_j = 0
for t in range(j+1):
sum_j += 2 ** t
mask = ~(sum_j - sum_i)
return (N & mask) | (M << i)mask=((1<<(j-i+1))-1)<<i;
mask=~mask;
N&=mask;
M=M<<i;
return M|N;If up to 31 bits cannot represent the fraction, means the fraction cannot be represent accurately.
def printBin(self, num: float) -> str:
res, i = "0.", 31
while num > 0 and i:
num *= 2
if num >= 1:
res += '1'
num -= 1
else:
res += '0'
i -= 1
return res if not num else "ERROR"Using counter i is faster than testing the length of result
store previous number of 1 as pre, current number of 1 as cur
compare current result to pre + cur, get the bigger.
Finally we still should update result again
def reverseBits(self, num: int) -> int:
pre = 0
cur = 0
res = 1
for i in range(32):
if num & (1 << i):
cur += 1
else:
res = max(res, pre + cur)
# plus 1 means the bit that we can flip
pre = cur + 1
cur = 0
return max(res, pre + cur)Increase the num, count the number of '1', break the first number as next Decrease the num, count the number of '0', break the first number as pre
def findClosedNumbers(self, num: int) -> List[int]:
res = [-1, -1]
n = bin(num).count('1')
nex = num + 1
while nex <= 2 ** 32 and bin(nex).count('1') != n:
nex += 1
if nex <= 2 ** 32:
res[0] = nex
pre = num - 1
while pre >= 0 and bin(pre).count('1') != n:
pre -= 1
if pre >= 0:
res[1] = pre
return resA XOR B, then count the number of '1'. Note in python, before XOR, we need number & 0xffffffff, because negative in python is two's complementary number. First solution:
def convertInteger(self, A: int, B: int) -> int:
return bin((A & 0xffffffff) ^ (B & 0xffffffff)).count('1')To count the number of '1', we can also use
res = 0
c = A ^ B
for i in range(32):
res += c >> i & 1Because c >> i & 1 will get the last digit of c.
So the second solution:
def convertInteger(self, A: int, B: int) -> int:
res = 0
c = A ^ B
for i in range(32):
res += c >> i & 1
return resNote above solution didn't consider negative's two's complementary number, I don't know why it works for negative number.
To count the number of '1', we can also clear the '1' one by one from right to left. To do this we need to do C = C & (C - 1) # 清除最低位 '1'.
Third solution:
def convertInteger(self, A: int, B: int) -> int:
C = (A & 0xffffffff) ^ (B & 0xffffffff)
cnt = 0
while C != 0: # 不断翻转最低位直到为 0
C = C & (C - 1) # 清除最低位
cnt += 1
return cntdef exchangeBits(self, num: int) -> int:
odd = num & 0x55555555
even = num & 0xaaaaaaaa
return (odd << 1) | (even >> 1)Here is a trick, how to make a mask:
(1 << m1) - 1, 1 shift m1 bits, then minus 1 we get m1-1 bits 1 on the right: 00000....1111111
def drawLine(self, length: int, w: int, x1: int, x2: int, y: int) -> List[int]:
#
ans = [0] * length
wid = w // 32
n1, m1 = divmod(x1, 32)
n2, m2 = divmod(x2, 32)
# 将起始点和终止点之间对应的比特位置为-1
for i in range(wid * y + n1, wid * y + n2 + 1):
ans[i] = -1
# 如果x1不是32的整数倍,再用一个mask来与对应的数相与
if m1:
ans[wid * y + n1] &= (1 << (32 - m1)) - 1
# 终点所在的数与mask异或
ans[wid * y + n2] ^= (1 << (31 - m2)) - 1
return ansFibonacci Sequence, Dynamic programming.
At n stair, I have three way to here, from n-1, n-2, n-3, so the total ways coming n is Ways(n-1) + Ways(n-2) + Ways(n-3). We can get the value one by one from ways(1) = 1, ways(2) = 2, ways(3) = 4
def waysToStep(self, n: int) -> int:
if n == 1:
return 1
if n == 2:
return 2
tmp1, tmp2, tmp3 = 1, 2, 4
for i in range(3, n):
tmp1, tmp2, tmp3 = tmp2, tmp3, tmp1 + tmp2 + tmp3
tmp1 = tmp1 % 1000000007
tmp2 = tmp2 % 1000000007
tmp3 = tmp3 % 1000000007
return tmp3We only need to find one path, so after go further, we put an obstacle to it, preventing next path go to it, this saves the further detection.
def pathWithObstacles(self, obstacleGrid: List[List[int]]) -> List[List[int]]:
res = []
self.findPath(0, 0, obstacleGrid, res)
return res
def findPath(self, x, y, grid, res):
# If exceed downside, return false
if x >= len(grid):
return False
# if exceed rightside, return false
if y >= len(grid[0]):
return False
# if there is an obstacle, return false
if grid[x][y] == 1:
return False
# the blank is eligible
res.append([x, y])
# In order to improve the speed, after explore one blank, put an obstacle in it, prevent next path explore it.
grid[x][y] = 1
# if reached the destination, return true
if x == len(grid) - 1 and y == len(grid[0]) - 1:
return True
# If right or down side can go, the current blank return True
if self.findPath(x, y + 1, grid, res) or self.findPath(x + 1, y, grid, res):
return True
# If both right and downside are not passable, return false
res.remove(res[-1])
return FalseWe can also put an obstacle after detecting that right and down are both not passable.
Another trick of above program is, if self.findPath(x, y + 1, grid, res) return true, we don't need go self.findPath(x + 1, y, grid, res), shortcut of or, improving the speed of the program.
Precise solution:
def pathWithObstacles(self, obstacleGrid: List[List[int]]) -> List[List[int]]:
ans, r, c = [], len(obstacleGrid), len(obstacleGrid[0])
def f(path):
if not ans:
i, j = path[-1]
if not obstacleGrid[i][j]:
obstacleGrid[i][j] = 1
i < r - 1 and f(path + [[i + 1, j]])
j < c - 1 and f(path + [[i, j + 1]])
if (i, j) == (r - 1, c - 1):
ans.extend(path)
f([[0, 0]])
return ansThe idea of this is, binary search:
There is only one or none crossing between elements and y = x, except the starting point.
def findMagicIndex(self, nums: List[int]) -> int:
return self.binarySearch(0, len(nums) - 1, nums)
def binarySearch(self, start, end, list):
if start >= end:
return -1
mid = (start + end) // 2
if list[mid] == mid:
return mid
if list[mid] > mid:
return self.binarySearch(start, mid, list)
else:
return self.binarySearch(mid+1, end, list)There might be multiple crossing points, so there is no rules to search. But the question require the minimum index, so we can improve the time by finding left first, then go to right. --剪枝
def findMagicIndex(self, nums: List[int]) -> int:
return self.binarySearch(0, len(nums) - 1, nums)
def binarySearch(self, start, end, list):
if start > end:
return -1
# take right mid
mid = (start + end + 1) // 2
# first, check left
left = self.binarySearch(start, mid - 1, list)
if left != -1:
return left
# second, check middle
if list[mid] == mid:
return mid
# last, check right
return self.binarySearch(mid + 1, end, list)For example, [1,2,3] Step1: Add an empty list Step2: Visit 1, add 1 to all list of last step: [], [1] Step3: Visit 2, add 2 to all list of last step: [], [1], [2], [1,2] Step4: Visit 3, add 3 to all list of last step: [], [1], [2], [1,2], [3], [1,3],[2,3],[1,2,3] Done
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [[]]
for num in nums:
mid_temp = []
for i in range(len(res)):
# don't use the original i
temp = res[i].copy()
temp.append(num)
res.append(temp)
return resWe can transform iteration to recursion, we can use tail recursion.
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [[]]
self.recursion(0, nums, res)
return res
def recursion(self, i, list, res):
if i >= len(list):
return
for t in range(len(res)):
temp = res[t].copy()
temp.append(list[i])
res.append(temp)
self.recursion(i + 1, list, res)The idea of back tracking is going further to do something, then come back(redo) to do something else.
private void backtrack("原始参数") {
//终止条件(递归必须要有终止条件)
if ("终止条件") {
//一些逻辑操作(可有可无,视情况而定)
return;
}
// 尝试所有选择,在尝试下一个选择的时候, 撤销前一个选择
for (int i = "for循环开始的参数"; i < "for循环结束的参数"; i++) {
//一些逻辑操作(可有可无,视情况而定)
//做出选择
//递归
backtrack("新的参数");
//一些逻辑操作(可有可无,视情况而定)
//撤销选择
}
}In the current case:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
self.backTracking(0, nums, res, [])
return res
def backTracking(self, start, list, res, temp):
# Here we don't need a terminate condition because the for loop will terminate finally
# we append all path of temp, note we use the copy of the original list
res.append(temp.copy())
# iterate the elements we are going to add
for i in range(start, len(list)):
temp.append(list[i])
# we go further to explore more elements and path
self.backTracking(i+1, list, res, temp)
# after iterating current element, we move on to the next element, so we pop previous element.
temp.pop()If we want the subset of the set, every element has two choice, take or not take, therefor finally we will have 2^n subsets.
We can use n bits to represent the take or not take status, for example, 001 for [1,2,3] means only take the last element 3.
So how do we get all the combination of bits? we can start from 000, then increase by 1, to 111. We will take the elements according to the bit.
def subsets(self, nums: List[int]) -> List[List[int]]:
total = 2 ** len(nums)
res = []
for i in range(total):
temp = []
for j in range(len(nums)):
if (i >> j) & 1:
temp.append(nums[j])
res.append(temp)
return resif A is even: A * B = A//2 * B * 2 = A//2 * B + A//2 * B
if A is Odd A * B = A//2 * B + A//2 * B + B
A//2 * B is the recursion part.
def multiply(self, A: int, B: int) -> int:
if A == 0:
return 0
p = self.multiply(A >> 1, B)
if A & 1:
return p + p + B
return p + pBasically, we use B as weight, then count the 1 bits of A, add together:
def multiply(self, A: int, B: int) -> int:
res = 0
while A != 0:
# check if the last bit is 1
if A & 1:
res += B
# A // 2
A = A >> 1
# B * 2
B = B << 1
return resdef hanota(self, A: List[int], B: List[int], C: List[int]) -> None:
"""
Do not return anything, modify C in-place instead.
"""
n = len(A)
# Move n elements from A to C via B
self.move(n, A, B, C)
def move(self, n, A, B, C):
if n == 0:
return
# move n-1 elements from A to B via C
self.move(n-1, A, C, B)
# Move A top to C
C.append(A.pop())
# move n-1 elements from B to C via A
self.move(n-1, B, A, C)The difference from the power set is, power set don't count back, so it don't count same characters with different sequence. But Permutation count same characters with difference sequence, hence it count back. Here we don't go back mathematically, but we check if c in temp.
def permutation(self, S: str) -> List[str]:
res = []
temp1 = ''
def backTracking(temp, S):
for i in S:
if i not in temp:
temp = temp + i
if len(temp) == len(S):
res.append(temp)
break
backTracking(temp, S)
temp = temp[:-1]
backTracking(temp1, S)
return resLast question, we are checking if i already in temp, that's because there is no duplicate in S. We can also remove the checked character, then don't have to check if i already in temp. This way can also solve this question, and with a set to remove duplicated result.
def permutation(self, S: str) -> List[str]:
# using a set to remove duplicated results
res = set()
temp1 = ''
def backTracking(temp, S, n):
for i in S:
temp = temp + i
if len(temp) == n:
res.add(temp)
break
# S.replace(i, '', 1) can remove already checked character i
backTracking(temp, S.replace(i, '', 1), n)
temp = temp[:-1]
backTracking(temp1, S, len(S))
return list(res)For back tracking, we would better move stop condition to the beginning.
def permutation(self, S: str) -> List[str]:
res = set()
temp1 = ''
def backTracking(temp, S, n):
if len(temp) == n:
res.add(temp)
return
for i in S:
temp = temp + i
backTracking(temp, S.replace(i, '', 1), n)
temp = temp[:-1]
backTracking(temp1, S, len(S))
return list(res)The idea of non-duplicated result is, for every recursion layer, we don't take sam character more than once.
So we can have a visited to exclude the characters that we already take. In this way, we don't need the set to remove duplication.
def permutation(self, S: str) -> List[str]:
res = []
temp1 = ''
def backTracking(temp, S, n):
if len(temp) == n:
res.append(temp)
return
visited = ''
for i in S:
# if current i is duplicated with previous i, we skip it.
if i in visited:
continue
visited += i
temp = temp + i
backTracking(temp, S.replace(i, '', 1), n)
temp = temp[:-1]
backTracking(temp1, S, len(S))
return resWe are growing a string, every time we can only select '(' or ')', and the number of ')' cannot be more than '(', finally the number of '(' or ')' should be n.
def generateParenthesis(self, n: int) -> List[str]:
res = []
temp1 = ''
backTrack(temp1, n, n)
def backTrack(temp, n1, n2):
# if n1 > n2, means ')' is already more than '(', it's illegal
if n1 > n2:
return
# if n1 = n2 = 0, means '(' and ')' are used up, and they are equal
if n2 == 0 and n1 == 0:
res.append(temp)
return
# Now we have two choice, we are going to try both
if n1 > 0:
backTrack(temp + '(', n1 - 1, n2)
# Here implies temp = temp[:-1], but because we didn't change temp in last step, so we don't need to do it.
if n2 > 0:
backTrack(temp + ')', n1, n2 - 1)def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
old_color = image[sr][sc]
# If new color == old color, we don't do anything, otherwise it will stack overflow
if newColor == old_color:
return image
self.paint(image, sr, sc, newColor, old_color)
return image
def paint(self, image, sr, sc, new_color, old_color):
# If out of bounds, return
if not (0 <= sr < len(image) and 0 <= sr < len(image[0])):
return
# if current square is not connected, return
if image[sr][sc] != old_color:
return
# now it's connected, so paint to new color
image[sr][sc] = new_color
# Go to four directions. Here is actually back tacking
self.paint(image, sr + 1, sc, new_color, old_color)
self.paint(image, sr - 1, sc, new_color, old_color)
self.paint(image, sr, sc + 1, new_color, old_color)
self.paint(image, sr, sc - 1, new_color, old_color)It is Knapsack problem, specifically, complete Knapsack problem, means we can repeat each options.
First, the below is the solution of 08.11.
def waysToChange(self, n: int) -> int:
coins = [1, 5, 10, 25]
dp = [0] * (n + 1)
dp[0] = 1
for coin in coins:
for j in range(coin, n + 1):
dp[j] = (dp[j] + dp[j - coin]) % 1000000007
return dp[n]Next, let's talk about Knapsack problem.
We have items with volume:[v1, v2, v3...], weights: [w1, w2, w3...], we have a pack with volume V, So how do we put items into the pack, so that the total weights is the most.
Let's say volumes: [2,3,5,7] weights: [2,5,2,5]
- Create a table, columns are different volume in total, rows are, we are considering if put the item of the row.
The first row 0 to 10 means volume that we used start from 0 to 10. column means the items we collected.
For example, the number of table[i][j] means with the volume j, the most weight that we can put items i, i-1..., 1.
For example, table[7][3] = 7, that is, with items [2,3,5], volumes[2,5,2] and total volume 7, the most weight we can put is 7, that is items[3,5] with volumes[2,5]. We have other choice, for example, items[2,5] with volumes[2,2], the total volume will hold [2,2], but obviously its weight is less than [2,5].
So how do we get the most weight? The answer is step by step.
- Only consider put item 1, the first row, table[0][0] means with volume 0, we cannot put anything, so the most weight is 0.
- table[0][1], volume 1 cannot hold item 1, so the most weight is still 0.
- table[0][2], volume 2 can hold item 1, so the most weight is 2...
- table[1][3], we are considering whether put item 2, the volume is 3, if we take item 2, the rest volume is 3 - 3 = 0, means no more space for another item, and the weight will be 5. If we don't take item 2, the weight remains 2, obvious it's less, so we take item 2. So table[1][3] = 5.
- table[2][10], we are considering when volume is 10, whether put item 3 or not. If we put item 3, so the rest of the volume is 10 - 3 = 7, and the most of weight on volume = 7 is table[i-1][7] = 7, plus weight of item 2, so it will be 7 + 2 = 9, more than table[i-1][10], so table[2][10] = 9.
The formula is:
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - C[i]] + W[i])The implementation of 01 Knapsack solution is:
public int zeroOnePack(int V, int[] C, int[] W) {
// 防止无效输入
if ((V <= 0) || (C.length != W.length)) {
return 0;
}
int n = C.length;
// dp[i][j]: 对于下标为 0~i 的物品,背包容量为 j 时的最大价值
int[][] dp = new int[n + 1][V + 1];
// 背包空的情况下,价值为 0
dp[0][0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= V; ++j) {
if (j >= C[i - 1]) {
dp[i][j] = Math.max(dp[i-1][j], dp[i - 1][j - C[i - 1]] + W[i - 1]);
}
}
}
// 返回,对于所有物品(0~N),背包容量为 V 时的最大价值
return dp[n][V];
}If C is sorted by ascending, we can iterate columns from C[i-1]:
public int zeroOnePack(int V, int[] C, int[] W) {
// 防止无效输入
if ((V <= 0) || (C.length != W.length)) {
return 0;
}
int n = C.length;
// dp[i][j]: 对于下标为 0~i 的物品,背包容量为 j 时的最大价值
int[][] dp = new int[n + 1][V + 1];
// 背包空的情况下,价值为 0
dp[0][0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = C[i]; j <= V; ++j) {
dp[i][j] = Math.max(dp[i-1][j], dp[i - 1][j - C[i - 1]] + W[i - 1]);
}
}
// 返回,对于所有物品(0~N),背包容量为 V 时的最大价值
return dp[n][V];From the table, we see dp[i][j] relies on previous row and columns. We get [i][j] from [i-1][j - w] and [i-1][j]. If we only want to get the final row, we can have only one row data, and update it row by row, no need a matrix.
However, we must update the row from right to left. Just because we want to use the current row as previous row, we cannot change the value that we need for current cell. For example: row 1: 1,2,3,4,5,6,7,8,9 now we are getting row 2 from row 1, for example, we update row2[9], we need row1[9] and row1[5], we cannot change row1[5] before we update row2[9], so we cannot update row2 from left to right, but from right to left.
public int zeroOnePack(int V, int[] C, int[] W) {
// 防止无效输入
if ((V <= 0) || (C.length != W.length)) {
return 0;
}
int n = C.length;
// dp[i][j]: 对于下标为 0~i 的物品,背包容量为 j 时的最大价值
int[] dp = new int[n + 1];
// 背包空的情况下,价值为 0
dp[0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = V; j >= C[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - C[i]] + W[i]);
}
}For 01 Knapsack problem, every item, we can only take once.
Complete Knapsack problem is, we have a pack with volume V, we have items: [v1, v2, v3...], with weight[w1, w2, w3...], we can take every item infinite times.
It's kind of trade off, if item with same volume but different weight, we absolutely will take the higher weight one.
For complete Knapsack problem, we are getting table[i][j] from table[i-1][j] and table[i][j - vi], instead of table[i-1][j-vi].
To save space, we are still using an array, and because we don't need table[i-1][j-vi], we should iterate from left to right(in the second loop).
public int completePackOpt(int V, int[] C, int[] W) {
if (V == 0 || C.length != W.length) {
return 0;
}
int n = C.length;
int[] dp = new int[V + 1];
for (int i = 0; i < n; ++i) {
for (int j = C[i]; j <= V; ++j) {
dp[j] = Math.max(dp[j], dp[j - C[i]] + W[i]);
}
}
return dp[V];
}For 322. Coin Change, we are trying to use least coin to get the amount, so we treat each coin's weight as 1, value as it's worth, and finally we want the least weight.
So the starting point dp[0] = 0, amount 0 has 0 coins. then the rest of the table should be set Integer.MAX_VALUE, and comparing with function min()
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int i = 0; i < coins.length; ++i) {
for (int j = coins[i]; j <= amount; ++j) {
if (dp[j - coins[i]] != Integer.MAX_VALUE) {
dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];
}def merge(self, A: List[int], m: int, B: List[int], n: int) -> None:
i, j = 0, 0
while j < n and i < m:
# If B[i] < A[i], swap
if A[i] > B[j]:
A[i], B[j] = B[j], A[i]
k = j
# After swap, try to bubble up the swapped element to right
while (k + 1) < n and B[k] > B[k + 1]:
B[k], B[k + 1] = B[k + 1], B[k]
k += 1
i += 1
# After swap, append B to A
i = m
while i < m + n:
A[i] = B[i - m]
i += 1Previously, if merge two sorted array, we create another array, then scan A and B, put them to the third array.
Now we have to merge A and B to bigger array, A. We cannot scan from left to right, because the if A[i] is bigger, it will be override. So we should scan A and B from right to left, and put them to the empty part of A.
def merge(self, A: List[int], m: int, B: List[int], n: int) -> None:
"""
Do not return anything, modify A in-place instead.
"""
i = m + n - 1
while m > 0 and n > 0:
if A[m - 1] > B[n - 1]:
A[i] = A[m - 1]
m -= 1
else:
A[i] = B[n - 1]
n -= 1
i -= 1
while m > 0:
A[i] = A[m - 1]
m -= 1
i -= 1
while n > 0:
A[i] = B[n - 1]
n -= 1
i -= 1public List<List<String>> groupAnagrams(String[] strs) {
List<List<String>> res = new ArrayList<>();
OuterLoop:
for (String str : strs) {
for (List<String> re : res) {
if (checkAnagram(re.get(0), str)) {
re.add(str);
continue OuterLoop;
}
}
// if not retrun in the loop, means we don't find a group
// for str, therefore we create a new one
res.add(new ArrayList<>().add(str));
}
return res;
}
/**
* using an array to check if two string are anagrams
* @param s1
* @param s2
* @return
*/
private boolean checkAnagram(String s1,
String s2) {
if (s1.length() != s2.length()) {
return false;
}
int[] dic = new int[128];
for (int i = 0; i < s1.length(); i++) {
dic[s1.charAt(i)]++;
}
for (int i = 0; i < s2.length(); i++) {
dic[s2.charAt(i)]--;
}
for (int i : dic) {
if (i != 0) {
return false;
}
}
return true;
}We can also sort each string, so that anagrams have same string, then use a hash map to store each group.
public List<List<String>> groupAnagrams(String[] strs) {
List<List<String>> res=new ArrayList<>();
Map<String,List<String>> map=new HashMap<>();
for(String s:strs)
{
char[] t=s.toCharArray();
Arrays.sort(t);
String string=String.valueOf(t);//将字符串全部化为按字典序排列,排序后相同的即为变位词
if(!map.containsKey(string))
map.put(string,new ArrayList<>());
map.get(string).add(s);
}
res.addAll(map.values());
return res;
}public int search(int[] arr,
int target) {
int start = 0;
int end = arr.length;
// this is the special case, [5,5,1,2,3,4,5], 5. Because in this case, we cannot split correctly, so we treat it as a special case.
if (arr[0] == arr[arr.length - 1] && target == arr[0]) {
return 0;
}
// Find the split point, get the offset
while (start < end) {
int mid = (start + end) / 2;
if (start == mid) {
start++;
break;
}
if (arr[mid] <= arr[start]) {
end = mid;
} else {
start = mid;
}
}
int offset = start;
return binarySearch(arr, 0, arr.length - 1, offset, target);
}
/**
* do normal binary search, note the elements may be duplicated, we want the match with the smallest index. So every time we <=, we go left to continue. And, we are using an offset, because the array is rotated. We search it as a normal ascending array, but we access element via offset.
*/
private int binarySearch(int[] arr,
int start,
int end,
int offset,
int target) {
if (arr[(start + offset) % arr.length] == target) {
return (start + offset) % arr.length;
}
if (start >= end) {
return -1;
}
int mid = (start + end) / 2;
int midLength = (mid + offset) % arr.length;
if (target > arr[midLength]) {
return binarySearch(arr, mid + 1, end, offset, target);
} else {
// smaller or equal, we will go left to searche
return binarySearch(arr, start, mid, offset, target);
}
}Still binary search, but because the mid may be empty string, so if it is empty string, we move start to right one position, check again, until we find a mid that is not empty string, then compare.
public int findString(String[] words,
String s) {
int left = 0, right = words.length;
while(left < right){
int mid = left + (right - left) / 2;
if(words[mid].equals("") && !words[left].equals(s)){
left++;
continue;
}else if(words[left].equals(s)){
return left;
}
if(words[mid].equals(s)){
return mid;
//mid在s后面
}else if(words[mid].compareTo(s) > 0){
right = mid;
//mid在s前面
}else if(words[mid].compareTo(s) < 0){
left = mid + 1;
}
}
return -1;
}[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
Look at the feature of the matrix, for [x][y], all [row <= x][col <= y] are smaller than [x][y], all [row >= x][col >= y] are greater than [x][y].
We want to start from one point, scan over the whole matrix, to find the target. If we start from [0][0] or [n][n], we don't know where to go for next step, because all rest elements are greater or smaller than [x][y].
If we start from [0][n], if current > target, we go up, if current < target, we go right. if current == target, return true.
If we start from [n][0], if current > target, we go left, if current < target, we go down. if current == target, return true.
We won't miss any row and colum, because every time it's either greater or smaller, finally we will find the target row and column.
public boolean searchMatrix(int[][] matrix, int target) {
int col = 0;
int row = matrix.length - 1;
while(row >= 0 && col< matrix[0].length){
if (matrix[row][col] < target){
col++;
}else if (matrix[row][col] > target){
row--;
}else {
return true;
}
}
return false;private static final int CPACITY = 500001;
int[] arr = new int[CPACITY];
public StreamRank() {
}
public void track(int x) {
arr[x]++;
}
public int getRankOfNumber(int x) {
int sum = 0;
for (int i = 0; i <= x; i++) {
sum += arr[i];
}
return sum;
}Like a snowball, every elements is the sum of previous elements, Original Array: A = [1,1,0,0,0,2,1,0,0,3,0..] to represent the number of the number (index) appeared.
Now we wanna know how many smallers appeared, so we wanna store the sum of previous elements. We create another array C.
C[1] = A[1]; C[2] = A[1] + A[2]; C[3] = A[3]; C[4] = A[1] + A[2] + A[3] + A[4]; C[5] = A[5]; C[6] = A[5] + A[6]; C[7] = A[7]; C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
So SUMi = C[i] + C[i-2k1] + C[(i - 2k1) - 2k2] + .....;
And if we want to update one element, we need to update all elements that are using it.
For example, if we wanna add A[1]++ , we must update C[1]++, C[2]++, C[4]++, C[8]++...
How do we know the indexes that we should update?
2 = 1+1 4 = 2+2 8 = 4+4
i_next = i + i&(-i)
private static final int CAPACITY = 500001;
int[] arr = new int[CAPACITY];
public StreamRank() {
}
public void track(int x) {
x++;
for (int i = x; i <= CAPACITY; i+= i &(-i)) {
arr[i]++;
}
}
public int getRankOfNumber(int x) {
x++;
int sum = 0;
for (int i = x; i > 0 ; i-=i&(-i)) {
sum+=arr[i];
}
return sum;
}public void wiggleSort(int[] nums) {
Integer[] boxed = new Integer[nums.length];
// in order to sort, we convert int array to integer array.
for (int i = 0; i < nums.length; i++) {
boxed[i] = nums[i];
}
Arrays.sort(boxed, new Comparator<Integer>() {
@Override
public int compare(Integer integer,
Integer t1) {
return t1.compareTo(integer);
}
});
// convert integer array back to int array
for (int i = 0; i < boxed.length; i++) {
nums[i] = boxed[i];
}
// swap every two elements, start from index 1
for (int i = 1; i < nums.length-1; i+=2) {
int temp = nums[i];
nums[i] = nums[i+1];
nums[i+1] = temp;
}
}We want something like [peak > valley < peak > valley < peak....] Note the even index we need it greater than last one, odd index we need it smaller than last one.
If we get odd peak2 and it's [peak1 > valley > peak2], because peak1 > peak2, we can just swap valley with peak2, so [peak1 > valley2 < peak']
If we get even valley2 and it's [valley1 < peak < valley2], because valley1 < valley2, we can just swap valley2 with peak, so [valley1 < peak2 > valley'].
public void wiggleSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
if ((i&1) == 1 && nums[i] > nums[i-1]){
int temp = nums[i];
nums[i] = nums[i-1];
nums[i-1] = temp;
}
if (((i&1) == 0) && nums[i] < nums[i-1]){
int temp = nums[i];
nums[i] = nums[i-1];
nums[i-1] = temp;
}
}
}Making use of A ^ B = C, then C ^ A = B or C ^ B = A. That is, C contains information of both A and B. We can use C with A to get B, or use C with B to get A.
public int[] swapNumbers(int[] numbers) {
numbers[0]^=numbers[1];
numbers[1]^=numbers[0];
numbers[0]^=numbers[1];
return numbers;
}numbers[0] = numbers[0] ^ numbers[1]
Now we have the original information of 0 and 1. (C)
With C and numbers[1], we can get numbers[0]
With C and numbers[0], we can get numbers[1], assign it back to numbers[0]
private Map<String, Integer> frequency = new HashMap();
public WordsFrequency(String[] book) {
for (String s : book) {
frequency.put(s, frequency.getOrDefault(s, 0) + 1);
}
}
public int get(String word) {
return frequency.getOrDefault(word, 0);
}public String tictactoe(String[] board) {
int n = board.length; // 说明是n*n的井字格
int xTotal = 0;
int yTotal = 0;
int left = 0; // 左上到右下的斜线
int right = 0; // 右上到坐下的斜线
// Flag to determine draw or pending at the end
boolean haveBlank = false;
// Check rows and columns
for (int i = 0; i < n; i++) {
// 表示第 i 行; 表示第 i 列。 两种理解。
xTotal = 0;
yTotal = 0;
for (int j = 0; j < n; j++) {
// 如果理解为第 i 行。
xTotal += board[i].charAt(j);
if (board[i].charAt(j) == ' ') haveBlank = true;
// 如果理解为第i列
yTotal += board[j].charAt(i);
}
if (xTotal == (int) 'X' * n || yTotal == (int) 'X' * n) return "X";
if (xTotal == (int) 'O' * n || yTotal == (int) 'O' * n) return "O";
left += board[i].charAt(i);
right += board[i].charAt(n - 1 - i);
}
// Check two cross, if their sum is n * X or O
if (left == (int) 'X' * n || right == (int) 'X' * n) return "X";
if (left == (int) 'O' * n || right == (int) 'O' * n) return "O";
if (haveBlank) return "Pending";
else return "Draw";
}Factorial is 1*2*3*4*5*6*..., equal to 1*2*3*2*2*5*2*3*..., whenever the result has a 0 at tail, means there is 2*5 appear, and because the number of 2 is always more than number of 5, so the number of 5 is the number of 0 at the tail. So the question becomes to how many 5 in the Prime factors of the factorial. So one factorial is 1*2*3*4*5...*n, till n, how many 5s? Whenever the n increase every 5, there is one more 5. So, the number of 5 in the Prime factors of the factorial is
while(n != 0){
number += n/5;
n/=5;
}So:
public int trailingZeroes(int n) {
int m5=0;
while(n>0){
n/=5;
m5+= n;
}
return m5;
}public int smallestDifference(int[] a, int[] b) {
Arrays.sort(a);
Arrays.sort(b);
int i = 0, j = 0;
int distance = - Math.abs(a[0] - b[0]);
while (i < a.length && j < b.length){
// here is using max, and negative abs, because if use min and positive abs, the distance can be out of range. (the problem of Math.abs(Integer.MIN_VALUE) = -2147483648)
distance = Math.max(distance, -Math.abs(a[i] - b[j]));
// improve the speed once the distance get 0
if (distance == 0) return 0;
if (a[i] < b[j]){
i++;
// improve the speed, skipping the smaller ones till the last smaller, we need to record that last smaller distance.
while ((i+1) < a.length && a[i+1] < b[j]) i++;
}else {
j++;
while ((j+1) < b.length && a[i] > b[j+1]) j++;
}
}
return -distance;
}](https://leetcode-cn.com/problems/maximum-lcci/)
let diff = a - b, if diff's sign bit is 1, means a < b, otherwise a > b. But in order to avoid a - b bit overflow, (it's possible, because for integer, the value range is -21......48 to + 21.......47, if a = -21......48, b = 1, a - b will be overflow), we use long to store the difference.
Finally, negatives >> 63 is -1 (shift with sign), positives >> 63 is 0, therefore, the final result is (diffSign bit + 1) * a - (diffSign bit * b).
public int maximum(int a, int b) {
long c = a;
long d = b;
long diff = c - d;
long diffSign = diff >> 63;
return (int)((diffPrime+1) * a - diffPrime *b);
}public int maxAliveYear(int[] birth, int[] death) {
int ans = -1;
int num = 0;//record the number of people
int max = num;//record the maximum of number
int i=0, j = 0;//index of birth and death
Arrays.sort(birth);
Arrays.sort(death);
// loop througth every year
for (int year = 1900; year <= 2000; year++){
//if current year exist in birth year, num++, i++;
while (i < birth.length && year == birth[i]){
num++;
i++;
}
//after counting the number of birth, we compare the number of people,
//if it's more than previous, we store the max number and year
if (num > max){
max = num;
ans = year;
}
//count the number of death
while (j < death.length && year == death[j]){
num--;
j++;
}
}
return ans;
}public int maxAliveYear(int[] birth, int[] death) {
// use an array to store each year birth and death
int[] changes = new int[102];
int len = birth.length, res = 1900, max_alive = 0, cur_alive = 0;
for (int i = 0; i < len; ++i) {
++changes[birth[i] - 1900];
--changes[death[i] - 1899];//because the people died in year x, he is counted alive in year x. But he is died in x+1 year.
}
// find the max.
for (int i = 1; i < 101; ++i) {
cur_alive += changes[i];
if (cur_alive > max_alive) {
max_alive = cur_alive;
res = 1900 + i;
}
}
return res;
}It's a very simple question, now we have two number, we are going to add k times, how many sum we can have? It's just k shorter, k-1 longer.... so on and so forth.
public int[] divingBoard(int shorter, int longer, int k) {
if (k == 0) return new int[0];
if (shorter == longer) return new int[]{k * shorter};
int[] ans = new int[k+1];
for (int i = 0; i < k+1; i++) {
ans[i] = longer * i + (k-i)*shorter;
}
return ans;
}we can also think about recursion, but because every iteration we add both shorter and longer, there are many duplication, we should remove those duplication.
For this problem, recursion will be over time.
The line cut two square evenly must across their center. So the line will be known.
To get the intersection of the line with squares, must check the slope of the line, if the slope > -1 and slope < 1, the intersections are with vertical edge. otherwise the intersections are with horizontal edges.
public double[] cutSquares(int[] square1, int[] square2) {
double[] center1 = new double[]{(square1[0] + (double)square1[2]/2), (square1[1] + (double)square1[2]/2)};
double[] center2 = new double[]{(square2[0] + (double)square2[2]/2), (square2[1] + (double)square2[2]/2)};
if (center1[0] == center2[0]){
double uppery1 = square1[1] + square1[2];
double uppery2 = square2[1] + square2[2];
return new double[]{center1[0], Math.min(square1[1], square2[1]), center2[0], Math.max(uppery1, uppery2)};
}
double a = (center1[1] - center2[1])/(center1[0] - center2[0]);
double b = center1[1] - a * center1[0];
if (a >= -1 && a <= 1){
double[] ans = new double[4];
ans[0] = Math.min(square1[0], square2[0]);
ans[1] = a * ans[0] + b;
ans[2] = Math.max(square1[0]+square1[2], square2[0]+square2[2]);
ans[3] = a * ans[2] + b;
return ans;
}
double[] ansP = new double[4];
ansP[3] = Math.min(square1[1], square2[1]);
ansP[1] = Math.max(square1[1] + square1[2], square2[1]+square2[2]);
ansP[0] = (ansP[1] - b)/a;
ansP[2] = (ansP[3] - b)/a;
if (ansP[0]> ansP[2]){
double x1 = ansP[0];
double y1 = ansP[1];
ansP[0]=ansP[2];
ansP[1]=ansP[3];
ansP[2]=x1;
ansP[3]=y1;
}
return ansP;
}public int[] masterMind(String solution, String guess) {
StringBuilder sb = new StringBuilder();
StringBuilder sb2 = new StringBuilder();
int[] ans = new int[2];
for (int i = 0; i < 4; i++) {
if (solution.charAt(i) == guess.charAt(i)){
ans[0]++;
}else {
sb.append(solution.charAt(i));
sb2.append(guess.charAt(i));
}
}
int[] chars = new int[128];
for (int i = 0; i < sb.length(); i++) {
chars[sb.charAt(i)]++;
}
for (int i = 0; i < sb2.length(); i++) {
if (chars[sb2.charAt(i)] > 0){
ans[1]++;
chars[sb2.charAt(i)]--;
}
}
return ans;
}public int[] subSort(int[] array) {
if(array == null || array.length == 0 || array.length == 1) return new int[]{-1,-1};
int m = 0 , n = array.length - 1;
//注意:数组中的数可能为负数
int min = Integer.MAX_VALUE , max = Integer.MIN_VALUE;
//max为乱序的最大值,min为乱序的最小值
for(int i = 0 ; i < array.length ; i++){
if(max <= array[i]){
max = array[i];
}else{
//记录乱序数组小于最大值的最大索引
m = i;
}
}
for(int j = array.length - 1 ; j >= 0 ; j--){
if(min >= array[j]){
min = array[j];
}else{
//记录乱序数组大于最大值的最小索引
n = j;
}
}
return m > n ? new int[]{n,m} : new int[]{-1,-1};
}Example: [1,2,4,7,10,11,7,12,6,7,16,18,19], the expected output: [3,9].
From right to left, we store the minimum, because if it's ascending, the minimum should greater or equal than current element, if not, means the minimum should go left, until we find a correct position for minimum.
On the right of index 3, the minimum is 6, 6 < current 7, so 6 should be on the left of 7, but 1,2,4 are all smaller than 6, therefore, the left index is 3.
The same thing for right index.
Brutal approach:
public int maxSubArray(int[] nums) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < nums.length; i++) {
int temMax = Integer.MIN_VALUE;
int sum = 0;
for (int i1 = i; i1 < nums.length; i1++) {
sum = sum + nums[i1];
if (sum > temMax){
temMax = sum;
}
}
if (temMax > max){
max = temMax;
}
}
return max;
}Need better solution...
public int[] pondSizes(int[][] land) {
int columns = land[0].length;
int rows = land.length;
List<Integer> ans = new ArrayList<>();
Set<Integer> visited = new HashSet<>();
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
int count = pond(land, i, j, visited);
// if current element count == 0, means either it's been visited or it's not 0
// if count != 0, means we find a pond
if (count != 0){
ans.add(count);
}
}
}
int[] ansP = ans.stream().mapToInt(i -> i).toArray();
Arrays.sort(ansP);
return ansP;
}
private int pond(int[][] land, int i, int j, Set<Integer> visited){
// if indexes are over boundary, we return 0
if (i < 0 || j < 0 || i >= land.length || j >= land[0].length) return 0;
// in order to track visited element, we give each element an unique index
int index = i * land[0].length + j;
// if visted, we don't count again
if (visited.contains(index)) return 0;
visited.add(index);
// if current != 0, means it's a boundary
if (land[i][j] != 0) return 0;
// we go through all the direction of current 0 element
int la = this.pond(land, i-1, j-1, visited);
int ll = this.pond(land, i, j-1, visited);
int lb = this.pond(land, i+1, j-1, visited);
int ma = this.pond(land, i-1, j, visited);
int mb = this.pond(land, i+1, j, visited);
int ra = this.pond(land, i-1, j+1, visited);
int rr = this.pond(land, i, j+1, visited);
int rb = this.pond(land, i+1, j+1, visited);
// we add all neighbors together and current self: 1
return la+ll+lb+ma+mb+ra+rr+rb+1;
}Above solution is kind of DFS, for each element, we detect all its neighbor(start from left above), if current element is not 0 or it's visited, we return 0.
we can also think of BFS, for each element, apply DFS. DFS can also find all possible connected 0.
BFS:
public int[] pondSizes(int[][] land) {
int columns = land[0].length;
int rows = land.length;
List<Integer> ans = new ArrayList<>();
Set<Integer> visited = new HashSet<>();
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
List<int[]> layer = new ArrayList<>();
int[] first = new int[2];
first[0] = i; first[1] = j;
layer.add(first);
int count = pond(land, visited, layer);
if (count != 0){
ans.add(count);
}
}
}
int[] ansP = ans.stream().mapToInt(i -> i).toArray();
Arrays.sort(ansP);
return ansP;
}
private int pond(int[][] land, Set<Integer> visited, List<int[]> layer){
if (layer.size() == 0) return 0;
int sum = 0;
List<int[]> nextLayer = new ArrayList<>();
for (int[] ints : layer) {
int i = ints[0], j = ints[1];
if (i < 0 || j < 0 || i >= land.length || j >= land[0].length) continue;
int index = i * land[0].length + j;
if (visited.contains(index)) continue;
visited.add(index);
if (land[i][j] != 0) continue;
nextLayer.add(new int[]{i-1, j-1});
nextLayer.add(new int[]{i, j-1});
nextLayer.add(new int[]{i+1, j-1});
nextLayer.add(new int[]{i-1, j});
nextLayer.add(new int[]{i+1, j});
nextLayer.add(new int[]{i-1, j+1});
nextLayer.add(new int[]{i, j+1});
nextLayer.add(new int[]{i+1, j+1});
sum = sum + 1;
}
return this.pond(land, visited, nextLayer) + sum;
}public List<String> getValidT9Words(String num,
String[] words) {
Map<Character, String> dic = new HashMap<>();
dic.put('2', "abc");
dic.put('3', "def");
dic.put('4', "ghi");
dic.put('5', "jkl");
dic.put('6', "mno");
dic.put('7', "pqrs");
dic.put('8', "tuv");
dic.put('9', "wxyz");
List<String> ans = new ArrayList<>();
// iterate words
for (String word : words) {
int i = 0;
// for each words, we check character and the coresponding number, if the number contains the character
for (; i < word.length(); i++) {
if (!dic.get(num.charAt(i)).contains(String.valueOf(word.charAt(i)))){
// if not contain, we break directly
break;
}
}
// check if all character is contained by number, if yes, add it to the answer list
if (i == word.length()){
ans.add(word);
}
}
return ans;
}- Find the difference of two sum;
- sort two arrays;
- two pointers, our goal is to find array1[pointer1] - array2[pointer2] * 2 == difference (because after swap, the sums difference = 2 * elements differences)
- if current element diff * 2 == sum difference, return;
- if current element diff * 2 < sum difference, move pointer1 forward;
- if current element diff * 2 > sum difference, move pointer2 forward;
public int[] findSwapValues(int[] array1, int[] array2) {
int sum1 = IntStream.of(array1).sum();
int sum2 = IntStream.of(array2).sum();
int difference = sum1 - sum2;
int[] array1_copy = array1.clone();
int[] array2_copy = array2.clone();
Arrays.sort(array1_copy);
Arrays.sort(array2_copy);
int i = 0, j = 0;
while (i<array1.length && j < array2.length){
int diff = (array1_copy[i] - array2_copy[j])*2;
if ( diff == difference){
return new int[]{array1_copy[i], array2_copy[j]};
}else if (diff < difference){
i++;
}else {
j++;
}
}
return new int[]{};
}- Put all visited coordinates to a hashmap, key is a Position object, value is the color
- create a counter-clock direction, if white block, index++ will be next direction, if black block, index--, will be the next direction.
- note the position object is going to be the key of hashmap, so, its hash() and equal() should be overridden.
- find the max and min colum and row, form a new string array.
private class Position{
private final int x;
private final int y;
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Position position = (Position) o;
return x == position.x && y == position.y;
}
@Override
public int hashCode() {
return Objects.hash(x, y);
}
Position (int x, int y){
this.x = x;
this.y = y;
}
public int getX() {
return x;
}
public int getY() {
return y;
}
}
public List<String> printKMoves(int K) {
int x = 0, y = 0;
Map<Position, String> board = new HashMap<>();
String[] directions = {"R","D", "L", "U"};
int[][] move = {{1,0}, {0,-1},{-1,0},{0, 1}};
int direction = 0;
int preCondition = 0;
while (K > 0){
Position currentPosition = new Position(x, y);
preCondition = direction;
if (board.containsKey(currentPosition) ){
if (board.get(currentPosition).equals("X")){
direction = (direction-1+4)%4;
board.put(currentPosition, "_");
}else {
direction = (direction+1)%4;
board.put(currentPosition, "X");
}
}else {
direction = (direction+1)%4;
board.put(currentPosition, "X");
}
x = x + move[direction][0];
y = y + move[direction][1];
K--;
}
board.put(new Position(x, y), directions[direction]);
int rowMin = Integer.MAX_VALUE;
int rowMax = Integer.MIN_VALUE;
int colMin = Integer.MAX_VALUE;
int colMax = Integer.MIN_VALUE;
for (Position position : board.keySet()) {
if (position.getY() >rowMax){
rowMax = position.getY();
}
if (position.getY() < rowMin){
rowMin = position.getY();
}
if (position.getX() > colMax){
colMax = position.getX();
}
if (position.getX() < colMin){
colMin = position.getX();
}
}
StringBuilder sb = new StringBuilder();
List<String> li = new ArrayList<>();
for (int j = rowMax; j >= rowMin; j--) {
for (int i = colMin; i <= colMax; i++) {
Position p = new Position(i, j);
sb.append(board.getOrDefault(p, "_"));
}
li.add(sb.toString());
sb.setLength(0);
}
String[] ans = new String[li.size()];
li.toArray(ans);
return li;
}- Sort array;
- Two pointers, one from 0, another from end;
- If curren two elements sum smaller than target, pointer1 increment, if bigger, pointer2 decrease, if equal, put elements into answer collection, pointer2 decrease and pointer1 increase at the same time.
public List<List<Integer>> pairSums(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> ans = new ArrayList<>();
int pointer2 = nums.length-1;
int pointer1 = 0;
while (pointer1 < pointer2){
if (nums[pointer1] + nums[pointer2] == target){
List<Integer> li = new ArrayList<>();
li.add(nums[pointer1]);
li.add(nums[pointer2]);
ans.add(li);
pointer1++;
pointer2--;
}else if (nums[pointer1] + nums[pointer2] > target){
pointer2--;
}else {
pointer1++;
}
}
return ans;
}- cache is a hash map
- Use a double linked hashmap to provide the order of the keys
- The most recent used key can be the head, vice versa.
- Implement own double linked list.
class LRUCache {
/**
* 双向链表数据类型
*/
static class Node{
int key,value;
Node prev,next;
public Node(int key,int value){
this.key = key;
this.value = value;
}
}
private Map<Integer,Node> map = new HashMap<>();
private Node head = new Node(-1,-1);
private Node tail = new Node(-1,-1);
private int k;
public LRUCache(int capacity) {
this.k = capacity;
head.next = tail;
tail.prev = head;
}
public int get(int key) {
if(map.containsKey(key)){
Node node = map.get(key);
removeNode(node);
moveToHead(node);
return node.value;
}
return -1;
}
public void put(int key, int value) {
if(get(key) > -1){
map.get(key).value = value;
}else{
if(map.size() == k){
int rk = tail.prev.key;
removeNode(tail.prev);
map.remove(rk);
}
Node node = new Node(key,value);
map.put(key,node);
moveToHead(node);
}
}
/**
* 移动节点到首位
*/
public void moveToHead(Node node){
node.next = head.next;
head.next.prev = node;
head.next = node;
node.prev = head;
}
/**
* 删除节点
*/
public void removeNode(Node node){
node.prev.next = node.next;
node.next.prev = node.prev;
}
}- Give each operator a weight, the weight of *, / are the same, greater than +, -. (if there is more complicated expression, we can assign more weight to more operators)
- whenever there is a number, push it to operands stack
- whenever there is an operator, compare it with the top of operator stack, if greater, push current operator to the stack as well. if smaller or equal, pop the two operands of the stack, use the top of the operator stack to calculate, push the result to operand stack.
- At the end, compute all the remained operators and operands. (the remained operators are from most to the least, we can calculate them from the top to the bottom)
public int calculate(String s) {
Stack<Character> operators = new Stack<>();
Stack<Integer> operands = new Stack<>();
HashMap<Character, Integer> operatorDic = new HashMap<>();
operatorDic.put('+', 1);
operatorDic.put('-', 1);
operatorDic.put('*', 2);
operatorDic.put('/', 2);
s = s.replaceAll("\\s", "");
int currentNum = 0;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c <=57 && c >=48){
currentNum = currentNum * 10 + c - 48;
}else {
operands.push(currentNum);
currentNum = 0;
while (!operators.isEmpty() && operatorDic.get(c) <= operatorDic.get(operators.peek())) {
int cal1 = cal(operands.pop(), operands.pop(), operators.pop());
operands.push(cal1);
}
operators.push(c);
}
}
operands.push(currentNum);
while (!operators.isEmpty()){
int cal = cal(operands.pop(), operands.pop(), operators.pop());
operands.push(cal);
}
return operands.pop();
}
private static int cal(int op1, int op2, char operator){
if (operator == '+'){
return op1 + op2;
}
if (operator == '-'){
return op2 - op1;
}
if (operator == '*'){
return op1 * op2;
}
if (operator == '/'){
return op2 / op1;
}
return 0;
}- a ^ b is the sum of a and b without carry
- (a & b) << 1 is the carry
- we add a ^ b and the carry, to get the sum, note now, there might still a carry, so we need to check, until the carry is not 1 any more.
public int add(int a, int b) {
while (b != 0){
int n = a ^ b;
b = (a & b) << 1;
a = n;
}
return a;
}public int missingNumber(int[] nums) {
int[] num = new int[nums.length+1];
for (int i : nums) {
num[i]++;
}
for (int i = 0; i < num.length; i++) {
if (num[i] == 0){
return i;
}
}
return -1;
}Idea: If a ^ b ^ b, we get a.
eg: [0,2,3], we define a res = 0; we use res xor all indexes from 0 to 2, finally xor nums.length.
if one index has index which is equal to it, then it will disappear.
res(0) ^ 0 ^ 0 ^ 1^ 2 ^ 2 ^ 3 ^ 3(length) = 1
public int missingNumber(int[] nums) {
int res = 0;
for(int i = 0; i < nums.length; i++){
res = res ^ i;
res = res ^ nums[i];
}
res = res ^ nums.length;
return res;
}public int missingNumber(int[] nums) {
int sumElement = 0;
int sumIndexes = 0;
for(int i : nums){
sumElement+=i;
}
for(int i = 0; i <= nums.length; i++){
sumIndexes += i;
}
return sumIndexes-sumElement;
}This approach can result in integer overflow.
- create another array with same length, dp
- this array will store the length of increasing array up to current index. e.g. dp[2] = 2 means up to array[2], the length of increasing array is 2. also means before index 2, there is only one element is smaller than array[2].
- iterate array dp, e.g, at index i, check how many elements are smaller than array[i], then dp[i] = Max(dp[j] + 1), note the index j, array[j] < array[i].
- For each outer iteration, record the biggest element.
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
int res = 1;
for (int i = 0; i < nums.length; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]){
//dp[i] = Max(dp[j] + 1)
if (1+dp[j]>dp[i] ){
dp[i] = dp[j] + 1;
}
}
}
if (dp[i] > res) res = dp[i];
}
return res;
}
}- Sort height and weight together ascending according to height
- if the same height, we sort weight descending order. The reason for this is that after sorting, we are going to find a increasing subset of weight, if the same height we have an ascending order, the increasing subset will have same duplicated height, which is not the correct answer.
class Solution {
public int bestSeqAtIndex(int[] height, int[] weight) {
int length = height.length;
int[][] com = new int[length][2];
for (int i = 0; i < length; i++) {
com[i][0] = height[i];
com[i][1] = weight[i];
}
Arrays.sort(com, (a, b) -> a[0] == b[0]? b[1] - a[1] : a[0] - b[0]);
int[] dp = new int[length];
int res = 1;
for (int i = 0; i < length; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (com[i][1] > com[j][1] ){
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}However, because the second step, finding the increasing weight subset is n^2 time complexity, above solution exceed the time limit.
For weight array, we want find a longest increasing sub-array. For each step, we build an array, if new coming element are greater than the most right, we add it to the array at the end, if new coming element are in the middle, we insert coming element to current array. Even though the finally array is not a correct increasing subset, but we can get the length of it.
eg. [5,3,2,5,6,1,3,4,5] dp: [5] (i=1) res = 1 [3] (i=2) res =1 [2] (i=3) res = 1 [2,5] (i=4) res = 2 [2,5,6] (i = 5) res = 3 [1,5,6] (i=6) (binarySearch find 1 should be insert in the index of 0, so we update index 0) res = 3 [1,3,6] (i = 7) (3 replace 5) [1,3,4] (i=8) (4 replace 6) [1,3,4,5] (i=9) res = 4
Note, every iteration, we binary search from index 0 to res.
class Solution {
public int bestSeqAtIndex(int[] height, int[] weight) {
int length = height.length;
int[][] com = new int[length][2];
for (int i = 0; i < length; i++) {
com[i][0] = height[i];
com[i][1] = weight[i];
}
Arrays.sort(com, (a, b) -> a[0] == b[0]? b[1] - a[1] : a[0] - b[0]);
int[] dp = new int[length];
dp[0] = com[0][1];
int res = 1;
for (int i = 1, j = 1; i < length; i++) {
//Arrays.binarySearch(dp, 0, res, com[i][1]) means do binary search on array dp to find com[i][1], from index 0 to res. If it find com[i][1], it will return its index, if not, it will return -shouldInsertIndex - 1, a negative number. we can get insert it by getting shouldInsertIndex = -(returnValue+1)
int i1 = Arrays.binarySearch(dp,0,res, com[i][1]);
if (i1 < 0) {
i1 = -(i1+1);
}
dp[i1] = com[i][1];
if (i1+1 > res) res = i1+1;
}
return res;
}
}1,3,5,7,9,15,21....
All elements are products of 3, 5, 7, so we form an array with those three factors in ascending order.
- Set three pointers, they start from index 1. On pointer3, the elements only times 3, on pointer5, the elements only times 5, on pointer7, the elements only times 7.
- Compare three pointer products, take the minimum one. If we take pointer3 * 3, then pointer3++, if take pointer5 * 5, pointer5++, if take pointer7 * 7, then pointer7++;
class Solution {
public int getKthMagicNumber(int k) {
int p3 = 0, p5 = 0, p7 = 0;
int[] arr = new int[k];
arr[0] = 1;
for (int i = 1; i < k; i++) {
arr[i] = Math.min(arr[p3]*3, Math.min(arr[p5]*5, arr[p7]*7));
if (arr[i] == arr[p3] * 3) p3++;
if (arr[i] == arr[p5] * 5) p5++;
if (arr[i] == arr[p7] * 7) p7++;
}
return arr[k-1];
}
}Require to be O(n) and space O(1)
Sort the array, get the middle element, but we need double check if it's the majority. This method takes at least nlog(n).
In an array, if we find two elements are different, we discard them. Finally, the left element might be the majority.
If an element is majority, the worst case is, its elements are dismissed by all other elements, but because it's majority, it will remain.
That is being said, many countries are in a war, if we say one vs one, finally, the most people country will win. The worst case is, all other country fight with the majority country, but majority country will still remain finally. Most case is, there are fights between other countries. The majority country doesn't lose the most people.
We use a count to represent the number of remained people.
- iterate the array, if count == 0, means so far no people remained, we assign current element as majority, count++.
- If count != 0, and if current element != majority, means there will be a fight, so count--. if current element == majority, means we are meeting a same element, we put it to the remained, so count++;
- After iteration, the majority will be remained. But we need to verify it. If it actually not a majority, means no majority. return -1.
class Solution {
public int majorityElement(int[] nums) {
int count = 0;
int major = 0;
for (int i = 0; i < nums.length; i++) {
if (count == 0){
major = nums[i];
count++;
}else {
if (major != nums[i]){
count--;
}else {
count++;
}
}
}
int c = 0;
for (int num : nums) {
if (num==temp) c++;
}
if (c>nums.length/2) return temp;
return -1;
}
}class Solution {
public int findClosest(String[] words, String word1, String word2) {
Map<String, List<Integer>> dic = new HashMap<>();
for (int i = 0; i < words.length; i++) {
if (dic.containsKey(words[i])){
dic.get(words[i]).add(i);
}else {
List<Integer> l = new ArrayList<>();
l.add(i);
dic.put(words[i], l);
}
}
List<Integer> integers1 = dic.get(word1);
List<Integer> integers2 = dic.get(word2);
int size1 = integers1.size();
int size2 = integers2.size();
int p1 = 0, p2 = 0;
int res = Integer.MAX_VALUE;
while (p1 < size1 && p2 < size2){
res = Math.min(res, Math.abs(integers1.get(p1) - integers2.get(p2)));
if (integers1.get(p1) < integers2.get(p2)){
p1++;
}else {
p2++;
}
}
return res;
}
}pointer1 search word1, pointer2 search word2, whenever find a word1 or word2, we calculate pointer1 - pointer2, get the minimum of the distance.
class Solution {
public int findClosest(String[] words, String word1, String word2) {
int pointer1 = -1, pointer2 = -1;
int dis = Integer.MAX_VALUE;
for (int i = 0; i < words.length; i++) {
if (words[i].equals(word1)){
pointer1 = i;
}
if (words[i].equals(word2)){
pointer2 = i;
}
if ( pointer1 != -1 && pointer2 != -1){
dis = Math.min(dis, Math.abs(pointer1-pointer2));
}
}
return dis;
}
}If we are going to query many times on same string, we would better use method 1, a Hashtable.
- In-order traverse
- On each node, set pre-node.right = current node, current.left = nul
- set pre = current node
We use a class field as pre node, the pre node keep changing with the traversal
class Solution {
private TreeNode head = null;
private TreeNode pre = null;
public TreeNode convertBiNode(TreeNode root) {
helper(root);
return head;
}
private void helper(TreeNode root) {
if (root == null) return;
helper(root.left);
if (pre == null) {
pre = root;
head = root;
} else {
pre.right = root;
pre = root;
}
root.left = null;
helper(root.right);
}
}Dynamic programming:
class Solution {
public int massage(int[] nums) {
if (nums.length == 0){
return 0;
}
int[][] arr = new int[nums.length][2];
arr[0][0] = 0;
arr[0][1] = nums[0];
for (int i = 1; i < nums.length; i++) {
arr[i][0] = Math.max(arr[i-1][0], arr[i-1][1]);
arr[i][1] = arr[i-1][0] + nums[i];
}
return Math.max(arr[nums.length-1][0], arr[nums.length-1][1]);
}
}Because arr[i][0] and arr[i][1] are only related to arr[i-1][0] and arr[i-1][1], so we can use two variables instead of two dimension array.
class Solution {
public int massage(int[] nums) {
if (nums.length == 0){
return 0;
}
int a = 0, b = nums[0];
for (int i = 1; i < nums.length; i++) {
int temp = b;
b = a + nums[i];
a = Math.max(a, temp);
}
return Math.max(a, b);
}
}def arrayManipulation(n, queries):
arr = [0] * (n + 1)
for query in queries:
arr[query[0] - 1] += query[2]
arr[query[1]] -= query[2]
# for i in range(len(arr) - 1):
# arr[i + 1] = arr[i] + arr[i + 1]
ans = -sys.maxsize
sum = 0
for i in arr:
sum+=i
if sum > ans:
ans = sum
return ans