0135.分发糖果.md

135. 分发糖果

力扣题目链接

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。
• 相邻的孩子中，评分高的孩子必须获得更多的糖果。

那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1: 输入: [1,0,2] 输出: 5 解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。

示例 2: 输入: [1,2,2] 输出: 4 解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。 第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

思路

这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼。

先确定右边评分大于左边的情况（也就是从前向后遍历）

此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果，全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果

局部最优可以推出全局最优。

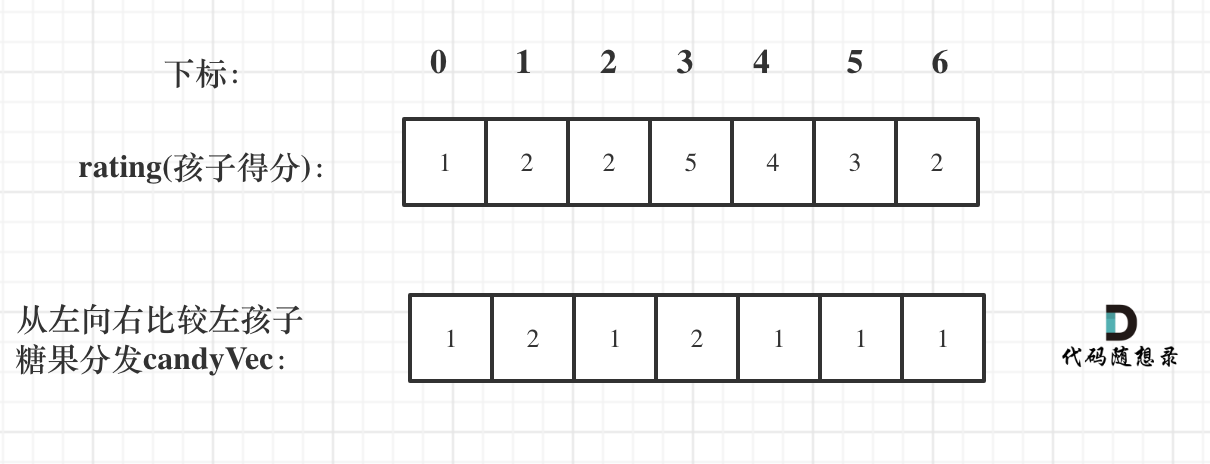
如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个，所以贪心：candyVec[i] = candyVec[i - 1] + 1

代码如下：

// 从前向后
for (int i = 1; i < ratings.size(); i++) {
    if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}

如图：

再确定左孩子大于右孩子的情况（从后向前遍历）

遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？

因为如果从前向后遍历，根据 ratings[i + 1] 来确定 ratings[i] 对应的糖果，那么每次都不能利用上前一次的比较结果了。

所以确定左孩子大于右孩子的情况一定要从后向前遍历！

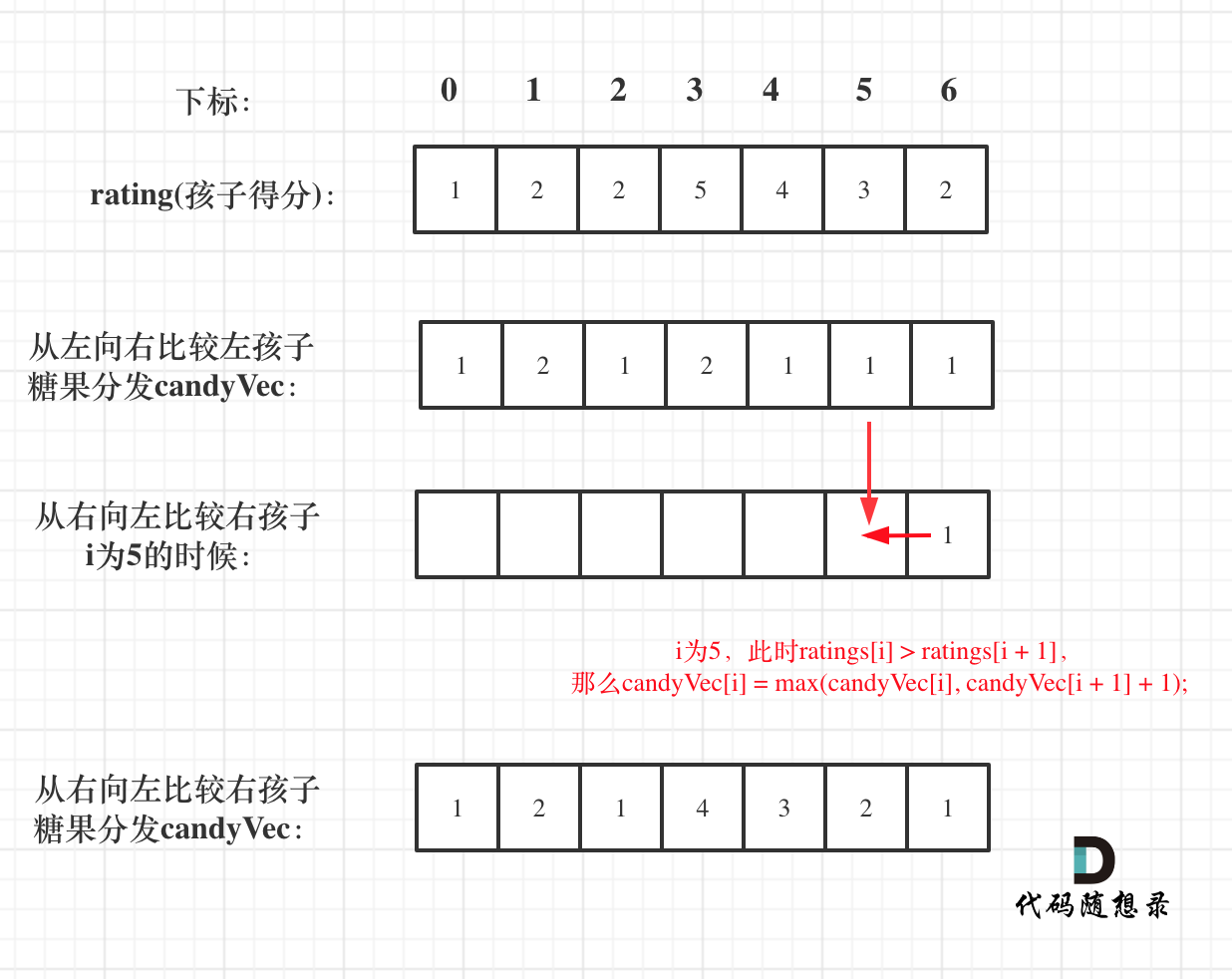
如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。

那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量即大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。

局部最优可以推出全局最优。

所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多，也比右边candyVec[i + 1]的糖果多。

如图：

所以该过程代码如下：

// 从后向前
for (int i = ratings.size() - 2; i >= 0; i--) {
    if (ratings[i] > ratings[i + 1] ) {
        candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
    }
}

整体代码如下：

class Solution {
public:
    int candy(vector<int>& ratings) {
        vector<int> candyVec(ratings.size(), 1);
        // 从前向后
        for (int i = 1; i < ratings.size(); i++) {
            if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
        }
        // 从后向前
        for (int i = ratings.size() - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1] ) {
                candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
            }
        }
        // 统计结果
        int result = 0;
        for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];
        return result;
    }
};

总结

这在leetcode上是一道困难的题目，其难点就在于贪心的策略，如果在考虑局部的时候想两边兼顾，就会顾此失彼。

那么本题我采用了两次贪心的策略：

• 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
• 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。

这样从局部最优推出了全局最优，即：相邻的孩子中，评分高的孩子获得更多的糖果。

其他语言版本

Java：

class Solution {
    /** 
         分两个阶段 
         1、起点下标1 从左往右，只要 右边 比 左边 大，右边的糖果=左边 + 1
         2、起点下标 ratings.length - 2 从右往左， 只要左边 比 右边 大，此时 左边的糖果应该 取本身的糖果数（符合比它左边大） 和 右边糖果数 + 1 二者的最大值，这样才符合 它比它左边的大，也比它右边大
    */
    public int candy(int[] ratings) {
        int[] candyVec = new int[ratings.length];
        candyVec[0] = 1;
        for (int i = 1; i < ratings.length; i++) {
            if (ratings[i] > ratings[i - 1]) {
                candyVec[i] = candyVec[i - 1] + 1;
            } else {
                candyVec[i] = 1;
            }
        }

        for (int i = ratings.length - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {
                candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);
            }
        }

        int ans = 0;
        for (int s : candyVec) {
            ans += s;
        }
        return ans;
    }
}

Python：

class Solution:
    def candy(self, ratings: List[int]) -> int:
        candyVec = [1] * len(ratings)
        for i in range(1, len(ratings)):
            if ratings[i] > ratings[i - 1]:
                candyVec[i] = candyVec[i - 1] + 1
        for j in range(len(ratings) - 2, -1, -1):
            if ratings[j] > ratings[j + 1]:
                candyVec[j] = max(candyVec[j], candyVec[j + 1] + 1)
        return sum(candyVec)

Go：

func candy(ratings []int) int {
    /**先确定一边，再确定另外一边
        1.先从左到右，当右边的大于左边的就加1
        2.再从右到左，当左边的大于右边的就再加1
    **/
    need:=make([]int,len(ratings))
    sum:=0
    //初始化(每个人至少一个糖果)
     for i:=0;i<len(ratings);i++{
         need[i]=1
     }
     //1.先从左到右，当右边的大于左边的就加1
    for i:=0;i<len(ratings)-1;i++{
        if ratings[i]<ratings[i+1]{
            need[i+1]=need[i]+1
        }
    }
    //2.再从右到左，当左边的大于右边的就右边加1，但要花费糖果最少，所以需要做下判断
    for i:=len(ratings)-1;i>0;i--{
        if ratings[i-1]>ratings[i]{
            need[i-1]=findMax(need[i-1],need[i]+1)
        }
    }
    //计算总共糖果
    for i:=0;i<len(ratings);i++{
        sum+=need[i]
    }
    return sum
}
func findMax(num1 int ,num2 int) int{
    if num1>num2{
        return num1
    }
    return num2
}

Javascript:

var candy = function(ratings) {
    let candys = new Array(ratings.length).fill(1)

    for(let i = 1; i < ratings.length; i++) {
        if(ratings[i] > ratings[i - 1]) {
            candys[i] = candys[i - 1] + 1
        }
    }

    for(let i = ratings.length - 2; i >= 0; i--) {
        if(ratings[i] > ratings[i + 1]) {
            candys[i] = Math.max(candys[i], candys[i + 1] + 1)
        }
    }
    
    let count = candys.reduce((a, b) => {
        return a + b
    })

    return count
};

---