Skip to content

Latest commit

 

History

History
180 lines (124 loc) · 9.88 KB

二叉树总结篇.md

File metadata and controls

180 lines (124 loc) · 9.88 KB
Raw

二叉树：总结篇！（需要掌握的二叉树技能都在这里了）

力扣二叉树大总结！

不知不觉二叉树已经和我们度过了三十三天，「代码随想录」里已经发了三十三篇二叉树的文章，详细讲解了30+二叉树经典题目，一直坚持下来的录友们一定会二叉树有深刻理解了。

在每一道二叉树的题目中，我都使用了递归三部曲来分析题目，相信大家以后看到二叉树，看到递归，都会想：返回值、参数是什么？终止条件是什么？单层逻辑是什么？

而且几乎每一道题目我都给出对应的迭代法，可以用来进一步提高自己。

下面Carl把分析过的题目分门别类，可以帮助新录友循序渐进学习二叉树，也方便老录友面试前快速复习，看到一个标题，就回想一下对应的解题思路，这样很快就可以系统性的复习一遍二叉树了。

公众号的发文顺序，就是循序渐进的，所以如下分类基本就是按照文章发文顺序来的，我再做一个系统性的分类。

二叉树的理论基础

二叉树的遍历方式

求二叉树的属性

  • 二叉树：是否对称
    • 递归：后序，比较的是根节点的左子树与右子树是不是相互翻转
    • 迭代：使用队列/栈将两个节点顺序放入容器中进行比较
  • 二叉树：求最大深度
    • 递归：后序，求根节点最大高度就是最大深度，通过递归函数的返回值做计算树的高度
    • 迭代：层序遍历
  • 二叉树：求最小深度
    • 递归：后序，求根节点最小高度就是最小深度，注意最小深度的定义
    • 迭代：层序遍历
  • 二叉树：求有多少个节点
    • 递归：后序，通过递归函数的返回值计算节点数量
    • 迭代：层序遍历
  • 二叉树：是否平衡
    • 递归：后序，注意后序求高度和前序求深度，递归过程判断高度差
    • 迭代：效率很低，不推荐
  • 二叉树：找所有路径
    • 递归：前序，方便让父节点指向子节点，涉及回溯处理根节点到叶子的所有路径
    • 迭代：一个栈模拟递归，一个栈来存放对应的遍历路径
  • 二叉树：递归中如何隐藏着回溯
  • 二叉树：求左叶子之和
    • 递归：后序，必须三层约束条件，才能判断是否是左叶子。
    • 迭代：直接模拟后序遍历
  • 二叉树：求左下角的值
    • 递归：顺序无所谓，优先左孩子搜索，同时找深度最大的叶子节点。
    • 迭代：层序遍历找最后一行最左边
  • 二叉树：求路径总和
    • 递归：顺序无所谓，递归函数返回值为bool类型是为了搜索一条边，没有返回值是搜索整棵树。
    • 迭代：栈里元素不仅要记录节点指针，还要记录从头结点到该节点的路径数值总和

二叉树的修改与构造

  • 翻转二叉树
    • 递归：前序，交换左右孩子
    • 迭代：直接模拟前序遍历
  • 构造二叉树
    • 递归：前序，重点在于找分割点，分左右区间构造
    • 迭代：比较复杂，意义不大
  • 构造最大的二叉树
    • 递归：前序，分割点为数组最大值，分左右区间构造
    • 迭代：比较复杂，意义不大
  • 合并两个二叉树
    • 递归：前序，同时操作两个树的节点，注意合并的规则
    • 迭代：使用队列，类似层序遍历

求二叉搜索树的属性

二叉树公共祖先问题

二叉搜索树的修改与构造

阶段总结

大家以上题目都做过了，也一定要看如下阶段小结。

每周小结都会对大家的疑问做统一解答，并且对每周的内容进行拓展和补充，所以一定要看，将细碎知识点一网打尽！

最后总结

在二叉树题目选择什么遍历顺序是不少同学头疼的事情，我们做了这么多二叉树的题目了，Carl给大家大体分分类。

  • 涉及到二叉树的构造，无论普通二叉树还是二叉搜索树一定前序，都是先构造中节点。

  • 求普通二叉树的属性，一般是后序，一般要通过递归函数的返回值做计算。

  • 求二叉搜索树的属性，一定是中序了，要不白瞎了有序性了。

注意在普通二叉树的属性中，我用的是一般为后序，例如单纯求深度就用前序，二叉树：找所有路径也用了前序，这是为了方便让父节点指向子节点。

所以求普通二叉树的属性还是要具体问题具体分析。

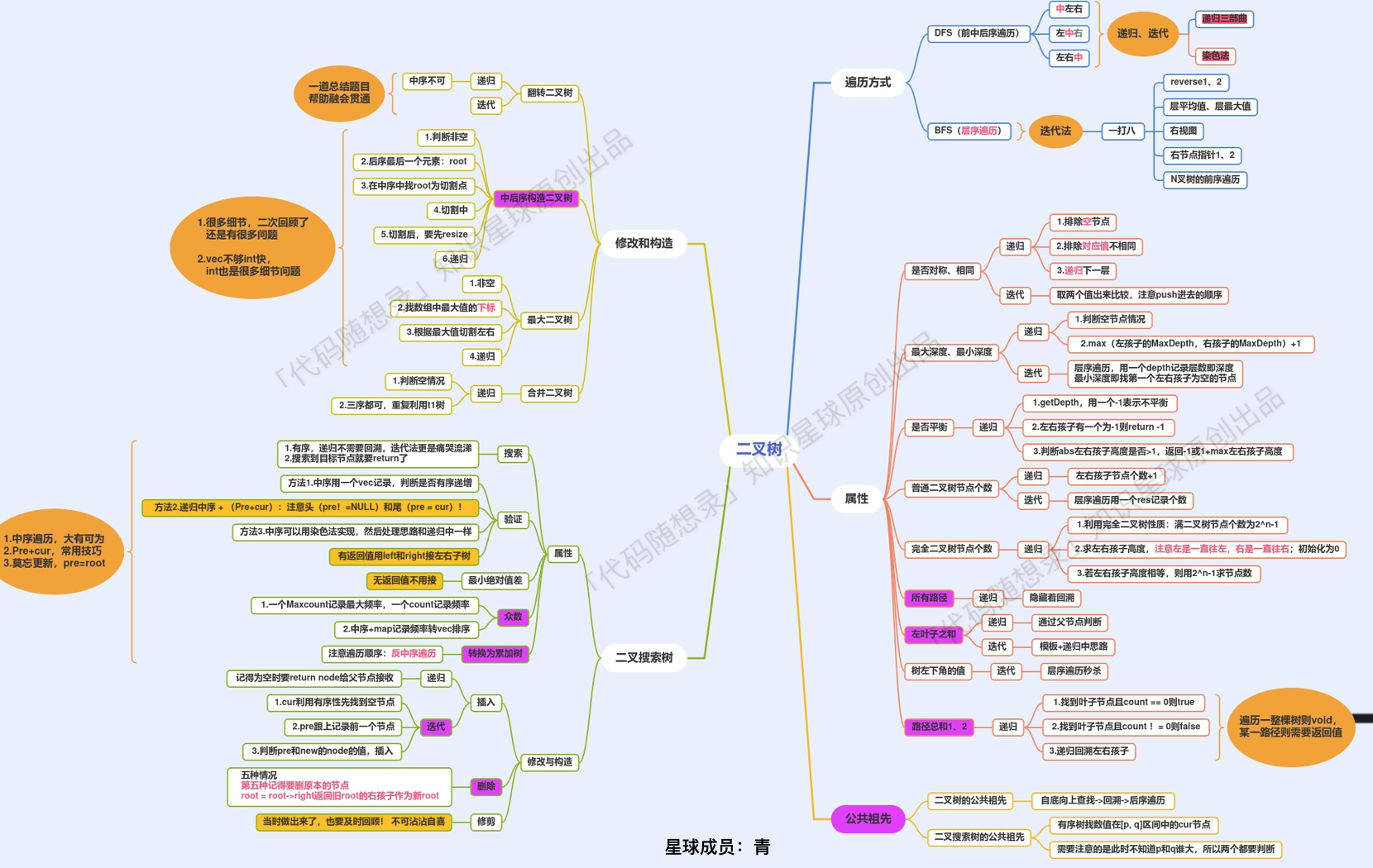
二叉树专题汇聚为一张图：

最后，二叉树系列就这么完美结束了，估计这应该是最长的系列了，感谢大家33天的坚持与陪伴，接下来我们又要开始新的系列了「回溯算法」！

其他语言版本

Java：

Python：

Go：